Published online by Cambridge University Press: 08 January 2021
We say that
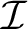 $\mathcal {I}$
is an ideal independent family if no element of
$\mathcal {I}$
is an ideal independent family if no element of
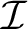 ${\mathcal {I}}$
is a subset mod finite of a union of finitely many other elements of
${\mathcal {I}}$
is a subset mod finite of a union of finitely many other elements of
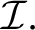 ${\mathcal {I}}.$
We will show that the minimum size of a maximal ideal independent family is consistently bigger than both
${\mathcal {I}}.$
We will show that the minimum size of a maximal ideal independent family is consistently bigger than both
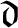 $\mathfrak {d}$
and
$\mathfrak {d}$
and
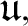 $\mathfrak {u},$
this answers a question of Donald Monk.
$\mathfrak {u},$
this answers a question of Donald Monk.
The first author was supported by CONACyT, scholarship 209499 and the second author gratefully acknowledge support from CONACyT grant A1-S-16164 and a PAPIIT grant IN 104220.