Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Fokina, Ekaterina B.
and
Friedman, Sy‐David
2012.
On Σ11 equivalence relations over the natural numbers.
Mathematical Logic Quarterly,
Vol. 58,
Issue. 1-2,
p.
113.
Bazhenov, N. A.
2013.
Computable Numberings of the Class of Boolean Algebras with Distinguished Endomorphisms.
Algebra and Logic,
Vol. 52,
Issue. 5,
p.
355.
Fokina, Ekaterina B.
Harizanov, Valentina
and
Melnikov, Alexander
2014.
Turing's Legacy.
p.
124.
Korovina, Margarita
and
Kudinov, Oleg
2015.
Perspectives of System Informatics.
Vol. 8974,
Issue. ,
p.
201.
Korovina, Margarita
and
Kudinov, Oleg
2015.
Evolving Computability.
Vol. 9136,
Issue. ,
p.
226.
KOROVINA, MARGARITA
and
KUDINOV, OLEG
2017.
Computable elements and functions in effectively enumerable topological spaces.
Mathematical Structures in Computer Science,
Vol. 27,
Issue. 8,
p.
1466.
Harrison-Trainor, Matthew
2018.
There is no classification of the decidably presentable structures.
Journal of Mathematical Logic,
Vol. 18,
Issue. 02,
p.
1850010.
Korovina, Margarita
and
Kudinov, Oleg
2018.
Perspectives of System Informatics.
Vol. 10742,
Issue. ,
p.
241.
HARRISON-TRAINOR, MATTHEW
2022.
AN INTRODUCTION TO THE SCOTT COMPLEXITY OF COUNTABLE STRUCTURES AND A SURVEY OF RECENT RESULTS.
The Bulletin of Symbolic Logic,
Vol. 28,
Issue. 1,
p.
71.
Calvert, Wesley
Harizanov, Valentina
and
Shlapentokh, Alexandra
2024.
Computability in infinite Galois theory and algorithmically random algebraic fields.
Journal of the London Mathematical Society,
Vol. 110,
Issue. 5,

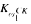 of structures of Scott rank
of structures of Scott rank 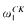 , the class
, the class 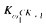 , of structures of Scott rank
, of structures of Scott rank 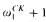 , and the class
, and the class 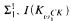 is
is  relative to Kleene's
relative to Kleene's 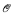 and
and 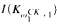 is
is 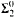 relative to
relative to 