Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
., Shanaz Ansari Wahid
., Norris Sookoo
and
., Ashok Sahai
2007.
Lattices of SK-Partitions.
Journal of Applied Sciences,
Vol. 7,
Issue. 16,
p.
2366.
Binns, Stephen
Kjos-Hanssen, Bjørn
Lerman, Manuel
Schmerl, James H.
and
Solomon, Reed
2008.
Self-Embeddings of Computable Trees.
Notre Dame Journal of Formal Logic,
Vol. 49,
Issue. 1,
Harizanov, Valentina S.
Jockusch, Carl G.
and
Knight, Julia F.
2009.
Chains and antichains in partial orderings.
Archive for Mathematical Logic,
Vol. 48,
Issue. 1,
p.
39.
Cenzer, Douglas
Harizanov, Valentina
Marker, David
and
Wood, Carol
2009.
Preface.
Archive for Mathematical Logic,
Vol. 48,
Issue. 1,
p.
1.
Parrochia, Daniel
and
Neuville, Pierre
2013.
Towards a General Theory of Classifications.
p.
229.
Fokina, Ekaterina B.
Harizanov, Valentina
and
Melnikov, Alexander
2014.
Turing's Legacy.
p.
124.
Jockusch, Carl G.
2017.
Computability and Complexity.
Vol. 10010,
Issue. ,
p.
127.
Fiori-Carones, Marta
Shafer, Paul
and
Soldà, Giovanni
2021.
An inside/outside Ramsey theorem and recursion theory.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 3,
p.
1977.
CERVELLE, JULIEN
GAUDELIER, WILLIAM
and
PATEY, LUDOVIC
2024.
THE REVERSE MATHEMATICS OF
${\mathsf {CAC\ FOR\ TREES}}$
.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 3,
p.
1189.

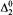 chain or an infinite
chain or an infinite 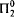 antichain. Our main result is that this cannot be improved: We construct an infinite computable partial ordering that has neither an infinite
antichain. Our main result is that this cannot be improved: We construct an infinite computable partial ordering that has neither an infinite 