Hostname: page-component-848d4c4894-ndmmz Total loading time: 0 Render date: 2024-06-12T21:39:26.688Z Has data issue: false hasContentIssue false
  • English
  • Français

Initial segments of the lattice of Π10 classes

Published online by Cambridge University Press:  12 March 2014

Douglas Cenzer  and
Andre Nies
Douglas Cenzer
Affiliation:
Department of Mathematics, University of Florida, Gainesville, FL 32611, USA, E-Mail: cenzer@math.ufl.edu
Andre Nies
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL 60637, USA, E-Mail: nies@math.uchicago.edu
Get access Rights & Permissions [Opens in a new window]

Abstract.

We show that in the lattice 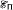of classes there are initial segments [∅, P] = 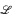(P) which are not Boolean algebras, but which have a decidable theory. In fact, we will construct for any finite distributive lattice L which satisfies the dual of the usual reduction property a class P such that L is isomorphic to the lattice 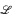(P)*, which is 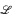(P). modulo finite differences. For the 2-element lattice, we obtain a minimal class, first constructed by Cenzer, Downey, Jockusch and Shore in 1993. For the simplest new class P constructed, P has a single, non-computable limit point and 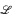(P)* has three elements, corresponding to ∅, P and a minimal class P0 ⊂ P, The element corresponding to P0 has no complement in the lattice. On the other hand, the theory of 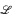(P) is shown to be decidable.

A class P is said to be decidable if it is the set of paths through a computable tree with no dead ends. We show that if P is decidable and has only finitely many limit points, then 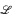(P)* is always a Boolean algebra. We show that if P is a decidable class and 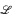(P) is not a Boolean algebra, then the theory of 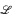(P) interprets the theory of arithmetic and is therefore undecidable.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 66 , Issue 4 , December 2001 , pp. 1749 - 1765
Copyright
Copyright © Association for Symbolic Logic 2001

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Burris, S. and Sankappanavar, H. P., Lattice-theoretic decision problems in universal algebras, Algebra Universalis, vol. 5 (1975), pp. 163–177.CrossRefGoogle Scholar
[2]Cenzer, D., classes in computability theory, Handbook of computability (Griffor, E., editor), Studies in Logic, no. 140, North-Holland, 1999, pp. 37–85.CrossRefGoogle Scholar
[3]Cenzer, D., Downey, R., Jockusch, C., and Shore, R., Countable thin classes, Annals of Pure and Applied Logic, vol. 59 (1993), pp. 79–139.CrossRefGoogle Scholar
[4]Cenzer, D. and Jockusch, C., classes – structure and application, Proceedings of the Boulder American Mamthematical Society conference (Lerman, M., editor), Contemporary Mathematics, American Mathematical Society, to appear.Google Scholar
[5]Cenzer, D. and Remmel, J., classes in mathematics, Handbook of recursive mathematics (Ershov, Y., Goncharov, S., Remmel, J., and Nerode, A., editors), Studies in Logic, no. 139, North-Holland, 1998, pp. 623–821.Google Scholar
[6]Downey, R., Maximal theories, Annals of Pure and Applied Logic, vol. 33 (1987), pp. 245–282.CrossRefGoogle Scholar
[7]Downey, R., Jockusch, C. G., and Stob, M., Array nonrecursive sets and multiple permitting arguments, Recursion theory week (Oberwolfach, March 1989) (Ambos-Spies, K., Muller, G., and Sacks, G. E., editors), Lecture Notes in Mathematics, no. 142, Springer, 1990, pp. 141–173.CrossRefGoogle Scholar
[8]Hermann, E.. Unpublished manuscript.Google Scholar
[9]Kripke, S. and Pour-El, M., Deduction-preserving recursive isomorphisms between theories, Fundamenta Mathematicae, vol. 61 (1967), pp. 141–163.Google Scholar
[10]Lachlan, A., On the lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 130 (1968), pp. 1–37.CrossRefGoogle Scholar
[11]Martin, D. and Pour-El, M., Axiomatizable theories with few axiomatizable extensions, this Journal, vol. 35 (1970), pp. 205–209.Google Scholar
[12]Nies, A., Intervals of the lattice of computably enumerable sets, Bulletin of the London Mathematical Society, vol. 29 (1997), pp. 683–692.CrossRefGoogle Scholar
[13]Nies, A., Effectively dense boolean algebras and their applications, Transactions of the American Mathematical Society, vol. 352 (2000), pp. 4989–5012.CrossRefGoogle Scholar
[14]Soare, R., Recursively enumerable sets and degrees, Springer-Verlag, 1987.CrossRefGoogle Scholar