Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Montalbán, Antonio
2009.
Mathematical Theory and Computational Practice.
Vol. 5635,
Issue. ,
p.
372.
Goncharov, S. S.
2011.
Degrees of autostability relative to strong constructivizations.
Proceedings of the Steklov Institute of Mathematics,
Vol. 274,
Issue. 1,
p.
105.
Ocasio-González, Víctor A.
2012.
How the World Computes.
Vol. 7318,
Issue. ,
p.
539.
Montalbán, Antonio
2012.
Rice sequences of relations.
Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 370,
Issue. 1971,
p.
3464.
Bazhenov*, N. A.
2013.
Degrees of categoricity for superatomic Boolean algebras.
Algebra and Logic,
Vol. 52,
Issue. 3,
p.
179.
Bazhenov, N. A.
and
Tukhbatullina, R. R.
2013.
Computable categoricity of the Boolean algebra $ \mathfrak{B}\left( \omega \right) $ with a distinguished automorphism.
Algebra and Logic,
Vol. 52,
Issue. 2,
p.
89.
Bazhenov, N. A.
2014.
Δ 2 0 -Categoricity of Boolean Algebras.
Journal of Mathematical Sciences,
Vol. 203,
Issue. 4,
p.
444.
Fokina, Ekaterina B.
Harizanov, Valentina
and
Melnikov, Alexander
2014.
Turing's Legacy.
p.
124.
Bazhenov, N. A.
2014.
Hyperarithmetical Categoricity of Boolean Algebras of Type B $$ \mathfrak{B} $$ (ω α × η).
Journal of Mathematical Sciences,
Vol. 202,
Issue. 1,
p.
40.
Johnson, J.
Knight, J. F.
Ocasio, V.
Tussupov, J.
and
VanDenDriessche, S.
2015.
Preserving Categoricity and Complexity of Relations.
Algebra and Logic,
Vol. 54,
Issue. 2,
p.
140.
Bazhenov, N. A.
2015.
2-Computably Enumerable Degrees of Categoricity for Boolean Algebras with Distinguished Automorphisms.
Journal of Mathematical Sciences,
Vol. 211,
Issue. 6,
p.
738.
Tussupov, J. A.
2015.
Categoricity and Complexity of Relations Over Algebraic Structures.
Algebra and Logic,
Vol. 54,
Issue. 5,
p.
408.
Downey, Rodney G.
Kach, Asher M.
Lempp, Steffen
Lewis-Pye, Andrew E.M.
Montalbán, Antonio
and
Turetsky, Daniel D.
2015.
The complexity of computable categoricity.
Advances in Mathematics,
Vol. 268,
Issue. ,
p.
423.
Alaev, P. E.
2015.
Ash’s Theorem on Δ α 0 -Categorical Structures and a Condition for Infinite Δ α 0 -Dimension.
Algebra and Logic,
Vol. 54,
Issue. 5,
p.
353.
Bazhenov, Nikolay
2017.
Theory and Applications of Models of Computation.
Vol. 10185,
Issue. ,
p.
85.
BAZHENOV, NIKOLAY
2018.
Autostability spectra for decidable structures.
Mathematical Structures in Computer Science,
Vol. 28,
Issue. 3,
p.
392.
Fokina, Ekaterina
Harizanov, Valentina
and
Turetsky, Daniel
2019.
Computability-theoretic categoricity and Scott families.
Annals of Pure and Applied Logic,
Vol. 170,
Issue. 6,
p.
699.
Bazhenov, N. A.
2021.
Categoricity Spectra of Computable Structures.
Journal of Mathematical Sciences,
Vol. 256,
Issue. 1,
p.
34.
Bazhenov, Nikolay
Fokina, Ekaterina
Rossegger, Dino
and
San Mauro, Luca
2021.
Degrees of bi-embeddable categoricity.
Computability,
Vol. 10,
Issue. 1,
p.
1.

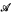 that is
that is 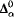 categorical, but not relatively
categorical, but not relatively 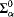 Scott family). We also show that for every computable limit ordinal
Scott family). We also show that for every computable limit ordinal 