Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hähnle, Reiner
2001.
Handbook of Philosophical Logic.
p.
297.
Halbach, Volker
2001.
Editorial Introduction.
Studia Logica,
Vol. 68,
Issue. 1,
p.
3.
Sazonov, Edward S.
Klinkhachorn, Powsiri
Gangarao, Hota V.S.
and
Halabe, Udaya B.
2002.
Fuzzy logic expert system for automated damage detection from changes in strain energy mode shapes.
Nondestructive Testing and Evaluation,
Vol. 18,
Issue. 1,
p.
1.
Field, Hartry
2002.
Saving the Truth Schema from Paradox.
Journal of Philosophical Logic,
Vol. 31,
Issue. 1,
p.
1.
Visser, Albert
2002.
Handbook of Philosophical Logic.
p.
149.
Field, Hartry
2003.
A Revenge-Immune Solution to the Semantic Paradoxes.
Journal of Philosophical Logic,
Vol. 32,
Issue. 2,
p.
139.
Hájek, Petr
and
Novák†, Vilém
2003.
The sorites paradox and fuzzy logic.
International Journal of General Systems,
Vol. 32,
Issue. 4,
p.
373.
Hájek, Petr
2005.
On arithmetic in the Cantor- Łukasiewicz fuzzy set theory.
Archive for Mathematical Logic,
Vol. 44,
Issue. 6,
p.
763.
Beall, J.
2006.
True, false and paranormal.
Analysis,
Vol. 66,
Issue. 2,
p.
102.
Hájek, Petr
2006.
A Companion to Philosophical Logic.
p.
595.
Rajati, Mohammad
Menhaj, Mohammad
and
Khaloozadeh, Hamid
2006.
An Extension to Zadeh's Truth Qualification Principle for Resolution of Self-Referential Sentences: Towards a Comprehensive Theory of Type-2 Fuzzy Possibility.
p.
1.
Malinowski, Gregorz
2007.
The Many Valued and Nonmonotonic Turn in Logic.
Vol. 8,
Issue. ,
p.
13.
Beall, JC
2007.
Philosophy of Logic.
p.
325.
LEITGEB, HANNES
2008.
ON THE PROBABILISTIC CONVENTION T.
The Review of Symbolic Logic,
Vol. 1,
Issue. 2,
p.
218.
Rajati, Mohammad Reza
Khaloozadeh, Hamid
and
Fatehi, Alireza
2009.
Intelligent Engineering Systems and Computational Cybernetics.
p.
209.
Andrea, Cantini
2009.
Logic from Russell to Church.
Vol. 5,
Issue. ,
p.
875.
Ivanitskii, Genrikh R.
2010.
21st century: what is life from the perspective of physics?.
Uspekhi Fizicheskih Nauk,
Vol. 180,
Issue. 4,
p.
337.
Cintula, Petr
and
Hájek, Petr
2010.
Triangular norm based predicate fuzzy logics.
Fuzzy Sets and Systems,
Vol. 161,
Issue. 3,
p.
311.
Yatabe, Shunsuke
2011.
New Frontiers in Artificial Intelligence.
Vol. 6797,
Issue. ,
p.
90.
Hájek, Petr
2011.
Proof, Computation and Agency.
p.
67.

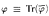 for all sentences φ? This problem is investigated in the frame of Łukasiewicz infinitely valued logic.
for all sentences φ? This problem is investigated in the frame of Łukasiewicz infinitely valued logic.