Article contents
Local behaviour of the Chebyshev theorem in models of I⊿0
Published online by Cambridge University Press: 12 March 2014
Extract
Let I⊿0 denote the fragment of Peano arithmetic where induction is restricted only to bounded formulas (⊿0-formulas), i.e. formulas where all the quantifiers are bounded. We will examine the behaviour in I⊿0 of Chebyshev's classical result on the distribution of primes. Chebyshev showed that each of the following functions on N is bounded by a polynomial in each of the others:
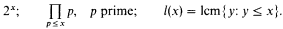
In his proof he used, as auxiliaries, factorials and binomial coefficients.
When we work in a weak system like I⊿0 we have to deal with two problems:
(i) There is not an immediate meaning for symbols like xy, Πp≤xp, and x!.
(ii) Some basic functions like exponentiation, factorial, and product of primes up to a certain element, are in general only partially definable.
The first problem is equivalent to finding ⊿0-formulas representing the relations z = xy, y = Πp≤xp, and y = x!. While we can easily express that y is the product of all primes less than or equal to x in a ⊿0-way, it requires a subtle argument to define z = xy by a ⊿0-formula. The most natural way of expressing it is via the formalization of the Chinese remainder theorem coding the recursion procedure used in the definition of xy. But this can be expressed only via a Σ1-formula. ⊿0-definitions of exponentiation were given by Paris and Bennett (see [GD] and [B]), and all sensible definitions of this type are equivalent (see Remark 1). Later we will examine properties of such a definition E0(x, y, z). The ⊿00-definition of y = Πp≤xp is much more straightforward, since both the relation of being a prime and the divisibility relation are ⊿0-definable. We will give an explicit definition of it and denote it by Ψ(x, y). In this way, by a ⊿0-induction, we will be able to prove the uniqueness of the elements y and z satisfying Ψ(x, y) and E0(x, y, z), respectively.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1992
References
REFERENCES
- 12
- Cited by

