Article contents
Logical paradoxes for many-valued systems
Published online by Cambridge University Press: 12 March 2014
Extract
As we know, the system of material implication is led into an inconsistency by the Russellian class, defined as λx. Nϵxx. This class, however, does no harm to many other systems, for example, the three-valued system L3 given by J. Łukasiewicz. A natural question is whether or not there exist classes which affect some of these other logical systems. The main result of the present paper is to answer this question affirmatively. At the end of this paper we point out that the interpretation given by J. Łukasiewicz for the system L3 is not satisfactory, and propose a new interpretation.
B. Russell deduced the mentioned inconsistency by the aid of the notion of negation. Later on, H. B. Curry pointed out that we could get the same result without the aid of that notion. None of these results affects the system L3 and other similar systems. But these systems may be involved.
To show this, we need the following definitions.
A function of two variables Cpq will be called an implication when the following “implication rule” is valid:
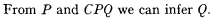
Under this definition we should note that material equivalence Epq, for example, is an implication.
Let C be such an implication. Then the symbol “(Cp)iq” is defined recursively by
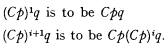
The class an is defined as λx. (Cϵxx)np, where p is a propositional variable. The rule of absorption of order n, denoted by (An), is:
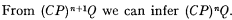
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1954
References
1 Whitehead, A. N. and Russell, B., Principia Mathematica, vol. 1Google Scholar, Introduction.
2 In the present paper we use Łukasiewicz's notation. Hence we write “ϵxy” instead of “xϵy.”
3 For the definitions of L3, Ln, and Lℵ0 see Łukasiewicz, J. and Tarski, A., Untersuchungen über den Aussagenkalkül, Comptes rendus des séances de la Société des Sciences et des Lettres de Varsovie, Classe III, vol. 23 (1930), pp. 30–50Google Scholar.
4 Łukasiewicz, J., Die Logik und das Grundlagenproblem, Les entretiens de Zürich sur les fondaments et la méthode des sciences mathématiques, 6–9 12 1938, Zürich, 1941Google Scholar.
5 Curry, H. B., The inconsistency of certain formal logics, this Journal, vol. 7 (1942), pp. 49–64Google Scholar.
6 Lewis, C. I. and Langford, C. H., Symbolic logic, New York, 1932Google Scholar.
7 Heyting, A., Die formalen Regeln dey intuitionistischen Logik, Sitzungsberichte der preussischen Akademie der Wissenschaften, Physikalisch-mathematische Klasse, 1930, pp. 42–56Google Scholar.
8 Johansson, I., Der Minimalkalkül, ein reduzierter intuitionistischer Formalismus, Compositio mathematica, vol. 4 (1936), pp. 119–136Google Scholar.
9 See Quine, W. V., Mathematical logic, second printing, Harvard University Press, Cambridge, Mass., 1947Google Scholar.
- 29
- Cited by

