Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-24T19:51:09.150Z Has data issue: false hasContentIssue false
  • English
  • Français

Logics without the contraction rule

Published online by Cambridge University Press:  12 March 2014

Hiroakira Ono  and
Yuichi Komori
Hiroakira Ono
Affiliation:
Hiroshima University, Hiroshima 730, Japan
Yuichi Komori
Affiliation:
Shizuoka University, Shizuoka 422, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

We will study syntactical and semantical properties of propositional logics weaker than the intuitionistic, in which the contraction rule (or, the exchange rule or the weakening rule, in some cases) does not hold. Here, the contraction rule means the rule of inference of the form

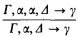
if we formulate our logics in a Gentzen-type formal system. Some syntactical properties of these logics have been studied firstly by the second author in [11], in connection with the study of BCK-algebras (for information on BCK-algebras, see [9]). There, it turned out that such a syntactical method is a powerful and promising tool in studying BCK-algebras. Using this method, considerable progress has been made since then (see, e.g., [8], [18], [27]).

In this paper, we will study these logics more comprehensively. We notice here that the distributive law

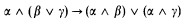
does not hold necessarily in these logics. By adding some axioms (or initial sequents) and rules of inference to these basic logics, we can obtain a lot of interesting nonclassical logics such as Łukasiewicz's many-valued logics, relevant logics, the intuitionistic logic and logics related to BCK-algebras, which have been studied separately until now. Thus, our approach will give a uniform way of dealing with these logics. One of our two main tools in doing so is Gentzen-type formulation of logics in syntax, and the other is semantics defined by using partially ordered monoids.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 50 , Issue 1 , March 1985 , pp. 169 - 201
Copyright
Copyright © Association for Symbolic Logic 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Chang, C.C., A new proof of the completeness of the Łukasiewicz axioms, Transactions of the American Mathematical Society, vol. 93 (1959), pp. 74–80.Google Scholar
[2] Fine, K., Models for entailment, Journal of Philosophical Logic, vol. 3 (1974), pp. 347–372.Google Scholar
[3] Grätzer, G., General lattice theory, Academic Press, New York, 1978.CrossRefGoogle Scholar
[4] Horn, A., The separation theorem of intuitionist propositional logics, this Journal, vol. 27 (1962), pp. 391–399.Google Scholar
[5] Hosoi, T., The separation theorem on the classical system, Journal of the Faculty of Science, University of Tokyo, Section 1, vol. 12 (1966), pp. 223–230.Google Scholar
[6] Hosoi, T. and Ono, H., Intermediate propositional logics (a survey), Journal of Tsuda College, vol. 5 (1973), pp. 67–82.Google Scholar
[7] Idziak, P. M., On varieties of BCK-algebras, Mathematica Japonica, vol. 28 (1983), pp. 157–162.Google Scholar
[8] Idziak, P. M., Lattice operation in BCK-algebras (to appear).Google Scholar
[9] Iseki, K. and Tanaka, S., An introduction to theory of BCK-algebras, Mathematica Japonica, vol. 23 (1978), pp. 1–26.Google Scholar
[10] Komori, Y., Super-Lukasiewicz propositional logics, Nagoya Mathematical Journal, vol. 84 (1981), pp. 119–133.CrossRefGoogle Scholar
[11] Komori, Y., The class of BCC-algebras is not a variety, Mathematica Japonica, vol. 29 (1984) (to appear).Google Scholar
[12] Komori, Y., The variety generated by BCC-algebras is finitely based, Reports of Faculty of Science, Shizuoka University, vol. 17 (1983), pp. 13–16.Google Scholar
[13] Komori, Y., Predicate logics without the structure rules (in preparation).Google Scholar
[14] Kripke, S., Semantical analysis of intuitionistic logic. I, Formal systems and recursive functions, North-Holland, Amsterdam, 1965, pp. 92–130.Google Scholar
[15] Krzystek, P. S., Commutative BCK-algebras do not enjoy the interpolation property, Polish Academy of Sciences, Institute of Philosophy and Sociology, Bulletin of the Section of Logic, vol. 12 (1983), pp. 50–54.Google Scholar
[16] Maksimova, L. L., Craig's theorem in superintuitionistic logics and amalgamable varieties of pseudo-Boolean algebras, Algebra i Logika, vol. 16(1977), pp. 643–681; English translation, Algebra and Logic , vol. 16 (1977), pp. 427–455.Google Scholar
[17] Ono, H., Semantical analysis of predicate logics without the contraction rule (to be submitted).Google Scholar
[18] Pałasiński, M., On BCK-algebras with the operation (S) (to appear).Google Scholar
[19] Rose, A. and Rosser, J. B., Fragments of many-valued statement calculi, Transactions of the American Mathematical Society, vol. 87 (1958), pp. 1–53.Google Scholar
[20] Routley, R. and Meyer, R. K., The semantics of entailment, Truth, syntax and modality, North-Holland, Amsterdam, 1973, pp. 199–243.Google Scholar
[21] Scott, D., Completeness and axiomatizability in many-valued logic, Proceedings of the Tarski Symposium, Proceedings of Symposia in Pure Mathematics, vol. 25, American Mathematical Society, Providence, Rhode Island, 1974, pp. 411–435.CrossRefGoogle Scholar
[22] Takeuti, G., Proof theory, Studies in Logic and the Foundations of Mathematics, vol. 81, North-Holland, Amsterdam, 1975.Google Scholar
[23] Urquhart, A., Semantics for relevant logics, this Journal, vol. 37 (1972), pp. 159–169.Google Scholar
[24] Urquhart, A., An interpretation of many-valued logic, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 19 (1973), pp. 111–114.Google Scholar
[25] Wronski, A., BCK-algebras do not form a variety, Mathematica Japonica, vol. 28 (1983), pp. 211–213.Google Scholar
[26] Wronski, A., Reflections and distensions of BCK-algebras, Mathematica Japonica, vol. 28 (1983), pp. 215–225.Google Scholar
[27] Wronski, A., Interpolation and amalgamation properties of BCK-algebras, Mathematica Japonica, vol. 29(1984), pp. 115–121.Google Scholar
[28] Dardžaniá, G. K., Intuitionistic system without contraction, Polish Academy of Sciences, Institute of Philosophy and Sociology, Bulletin of the Section of Logic, vol. 6 (1977), pp. 2–8.Google Scholar
[29] Tamura, S., On a decision procedure for free lo-algebraic systems, Technical Report of Mathematics, no. 9, Yamaguchi University, Yamaguchi, 1974.Google Scholar