Article contents
MARGINALIA ON A THEOREM OF WOODIN
Published online by Cambridge University Press: 21 March 2017
Abstract
Let 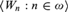 $\left\langle {{W_n}:n \in \omega } \right\rangle$ be a canonical enumeration of recursively enumerable sets, and suppose T is a recursively enumerable extension of PA (Peano Arithmetic) in the same language. Woodin (2011) showed that there exists an index
$\left\langle {{W_n}:n \in \omega } \right\rangle$ be a canonical enumeration of recursively enumerable sets, and suppose T is a recursively enumerable extension of PA (Peano Arithmetic) in the same language. Woodin (2011) showed that there exists an index 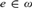 $e \in \omega$ (that depends on T) with the property that if
$e \in \omega$ (that depends on T) with the property that if 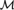 ${\cal M}$ is a countable model of T and for some
${\cal M}$ is a countable model of T and for some 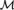 ${\cal M}$ -finite set s,
${\cal M}$ -finite set s, 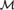 ${\cal M}$ satisfies
${\cal M}$ satisfies 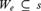 ${W_e} \subseteq s$ , then
${W_e} \subseteq s$ , then 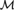 ${\cal M}$ has an end extension
${\cal M}$ has an end extension 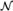 ${\cal N}$ that satisfies T + W e = s.
${\cal N}$ that satisfies T + W e = s.
Here we generalize Woodin’s theorem to all recursively enumerable extensions T of the fragment 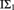 ${{\rm{I}\rm{\Sigma }}_1}$ of PA, and remove the countability restriction on
${{\rm{I}\rm{\Sigma }}_1}$ of PA, and remove the countability restriction on 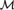 ${\cal M}$ when T extends PA. We also derive model-theoretic consequences of a classic fixed-point construction of Kripke (1962) and compare them with Woodin’s theorem.
${\cal M}$ when T extends PA. We also derive model-theoretic consequences of a classic fixed-point construction of Kripke (1962) and compare them with Woodin’s theorem.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 3
- Cited by

