Published online by Cambridge University Press: 17 April 2014
Our results in this paper increase the model-theoretic precision of a widely used
method for building ultrafilters, and so advance the general problem of
constructing ultrafilters whose ultrapowers have a precise degree of saturation.
We begin by showing that any flexible regular ultrafilter makes the product of
an unbounded sequence of finite cardinals large, thus saturating any stable
theory. We then prove directly that a “bottleneck” in the
inductive construction of a regular ultrafilter on λ
(i.e., a point after which all antichains of 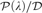 ${\cal P}\left( \lambda \right)/{\cal D}$ have cardinality less than λ)
essentially prevents any subsequent ultrafilter from being flexible, thus from
saturating any nonlow theory. The constructions are as follows. First, we
construct a regular filter
${\cal P}\left( \lambda \right)/{\cal D}$ have cardinality less than λ)
essentially prevents any subsequent ultrafilter from being flexible, thus from
saturating any nonlow theory. The constructions are as follows. First, we
construct a regular filter 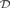 ${\cal D}$ on λ so that any ultrafilter
extending
${\cal D}$ on λ so that any ultrafilter
extending 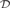 ${\cal D}$ fails to
${\cal D}$ fails to 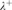 ${\lambda ^ + }$-saturate ultrapowers of the random graph, thus of any unstable
theory. The proof constructs the omitted random graph type directly. Second,
assuming existence of a measurable cardinal κ, we
construct a regular ultrafilter on
${\lambda ^ + }$-saturate ultrapowers of the random graph, thus of any unstable
theory. The proof constructs the omitted random graph type directly. Second,
assuming existence of a measurable cardinal κ, we
construct a regular ultrafilter on 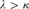 $\lambda > \kappa$ which is λ-flexible but not
$\lambda > \kappa$ which is λ-flexible but not 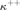 ${\kappa ^{ + + }}$-good, improving our previous answer to a question raised in
Dow (1985). Third, assuming a weakly compact cardinal
κ, we construct an ultrafilter to show that
${\kappa ^{ + + }}$-good, improving our previous answer to a question raised in
Dow (1985). Third, assuming a weakly compact cardinal
κ, we construct an ultrafilter to show that 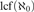 ${\rm{lcf}}\left( {{\aleph _0}} \right)$ may be small while all symmetric cuts of cofinality
κ are realized. Thus certain families of precuts
may be realized while still failing to saturate any unstable theory.
${\rm{lcf}}\left( {{\aleph _0}} \right)$ may be small while all symmetric cuts of cofinality
κ are realized. Thus certain families of precuts
may be realized while still failing to saturate any unstable theory.