Hostname: page-component-76c49bb84f-qtd2s Total loading time: 0 Render date: 2025-07-04T09:42:52.832Z Has data issue: false hasContentIssue false
  • English
  • Français

Omitting types in set theory and arithmetic

Published online by Cambridge University Press:  12 March 2014

Julia F. Knight
Julia F. Knight*
Affiliation:
Pennsylvania State University, University Park, Pennsylvania 16802
Get access Rights & Permissions [Opens in a new window]

Extract

In [7] it is shown that if Σ is a type omitted in the structure 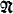= ω, +, ·, < and complete with respect to Th(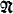) then Σ is omitted in models of Th(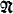) of all infinite powers. The proof given there extends readily to other models of P. In this paper the result is extended to models of ZFC. For pre-tidy models of ZFC, the proof is a straightforward combination of the methods in [7] and in Keisler and Morley ([9], [6]). For other models, the proof involves forcing. In particular, it uses Solovay and Cohen's original forcing proof that GB is a conservative extension of ZFC (see [2, p. 105] and [5, p. 77]).

The method of proof used for pre-tidy models of set theory can be used to obtain an alternate proof of the result for 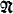This new proof yields more information. First of all, a condition is obtained which resembles the hypothesis of the “Omitting Types” theorem, and which is sufficient for a theory T to have a model omitting a type Σ and containing an infinite set of indiscernibles. The proof that this condition is sufficient is essentially contained in Morley's proof [9] that the Hanf number for omitting types is 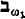so the condition will be called Morley's condition.

If T is a pre-tidy theory, Morley's condition guarantees that T will have models omitting Σ in all infinite powers.

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 41 , Issue 1 , March 1976 , pp. 25 - 32
Copyright
Copyright © Association for Symbolic Logic 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1] Baldwin, J. T. and Lachlan, A. H., On strongly minimal sets, this Journal, vol. 36 (1971), pp. 79–96.Google Scholar
[2] Cohen, P. J., Set theory and the continuum hypothesis, Benjamin, New York and Amsterdam, 1966.Google Scholar
[3] Ehrenfeucht, A. and Mostowski, A., Models of axiomatic theories admitting automorphisms, Fundamenta Mathematicae, vol. 43 (1956), pp. 50–68.Google Scholar
[4] Erdos, P. and Rado, R., A partition calculus in set theory, Bulletin of the American Mathematical Society, vol. 62 (1956), pp. 427–489.CrossRefGoogle Scholar
[5] Keisler, H. J., Model theory for infinitary logic, North-Holland, Amsterdam, 1971.Google Scholar
[6] Keisler, H. J. and Morley, M., Elementary extensions of models of set theory, Israel Journal of Mathematics, vol. 6 (1968), pp. 49–65.CrossRefGoogle Scholar
[7] Knight, J., Types omitted in uncountable models of arithmetic, this Journal, vol. 40 (1975), pp. 317–320.Google Scholar
[8] Morley, M., Categoricity in power, Transactions of the American Mathematical Society, vol. 114 (1965), pp. 514–538.CrossRefGoogle Scholar
[9] Morley, M., Omitting classes of elements, The theory of models (Proceedings of the 1963 Symposium at Berkeley), North-Holland, Amsterdam, 1965, pp. 265–273.Google Scholar