Article contents
On a condition for Cohen extensions which preserve precipitous ideals
Published online by Cambridge University Press: 12 March 2014
Extract
T. Jech and K. Prikry introduced the concept of precipitous ideals as a counterpart of measurable cardinals for small cardinals (Jech and Prikry [1]). To get a precipitous ideal on ℵ1( W. Mitchell used the Cohen extension by the standard Levy collapse that makes κ = ℵ1, where κ is a measurable cardinal in the ground model (Jech, Magidor, Mitchell and Prikry [2]). His proof essentially used the fact that 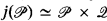 , where
, where 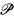 is the notion of forcing of Levy collapse and j is the elementary embedding obtained by a normal ultrafilter on κ.
is the notion of forcing of Levy collapse and j is the elementary embedding obtained by a normal ultrafilter on κ.
On the other hand, we know that 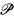 has the κ-chain condition. In this paper, we show that the κ-chain condition for notions of forcing plays an essential role for preserving normal precipitous ideals. Namely,
has the κ-chain condition. In this paper, we show that the κ-chain condition for notions of forcing plays an essential role for preserving normal precipitous ideals. Namely,
Theorem 1. Let κ be a regular uncountable cardinal and I a normal ideal on κ. Let 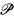 be a notion of forcing with the κ-chain condition. Then, I is precipitous iff ⊩“the ideal on κ generated by I is precipitous”.
be a notion of forcing with the κ-chain condition. Then, I is precipitous iff ⊩“the ideal on κ generated by I is precipitous”.
As an application of Theorem 1, we have the following theorem.
Theorem 2. Let κ be a regular uncountable cardinal, and Γ be a κ-saturated normal ideal on κ. Then, {a < κ; the ideal of thin sets on a is precipitous} has either Γ-measure one or Γ-measure zero, and the ideal of thin sets on κ is precipitous iff {α< κ; the ideal of thin sets on α is precipitous) has Γ-measure one.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1981
References
REFERENCES
- 14
- Cited by

