Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Ehrenfeucht, A.
and
Feferman, S.
1960.
Representability op recursively enumerable sets in formal theories.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 5,
Issue. 1-2,
p.
37.
Smullyan, Raymond M.
1960.
Theories with Effectively Inseparable Nuclei.
Mathematical Logic Quarterly,
Vol. 6,
Issue. 15-22,
p.
219.
Przeŀęcki, Marian
1961.
Pojęcia teoretyczne a doświadczenie.
Studia Logica,
Vol. 11,
Issue. 1,
p.
91.
Lévy, Azriel
1961.
Axiomization of induced theories.
Proceedings of the American Mathematical Society,
Vol. 12,
Issue. 2,
p.
251.
Feferman, S.
Kreisel, G.
and
Orey, S.
1962.
1 — Consistency and faithful interpretations.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 6,
Issue. 1-2,
p.
52.
Wójcicki, Ryszard
1963.
Analityczne komponenty definicji arbitralnych.
Studia Logica,
Vol. 14,
Issue. 1,
p.
119.
Przełęcki, Marian
1963.
O pojęciu zdania analitycznego.
Studia Logica,
Vol. 14,
Issue. 1,
p.
155.
Schwabhäuser, Wolfram
1967.
Zur axiomatisierbarkeit von theorien in der schwachen logik der zweiten stufe.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 10,
Issue. 3-4,
p.
60.
Hooker, C. A.
1968.
Five arguments against Craigian transcriptionism.
Australasian Journal of Philosophy,
Vol. 46,
Issue. 3,
p.
265.
Kreisel, G.
and
Lévy, A.
1968.
Reflection Principles and their Use for Establishing the Complexity of Axiomatic Systems.
Mathematical Logic Quarterly,
Vol. 14,
Issue. 7-12,
p.
97.
Jones, J. P.
1969.
Independent recursive axiomatizability in arithmetic.
Proceedings of the American Mathematical Society,
Vol. 23,
Issue. 1,
p.
107.
Montague, Richard
1970.
Pragmatics and Intensional Logic.
Dialectica,
Vol. 24,
Issue. 4,
p.
277.
Montague, Richard
1970.
Pragmatics and intensional logic.
Synthese,
Vol. 22,
Issue. 1-2,
p.
68.
Case, John
1971.
Enumeration reducibility and partial degrees.
Annals of Mathematical Logic,
Vol. 2,
Issue. 4,
p.
419.
Jeroslow, R. G.
1971.
Non‐Effectiveness in S. Orey's Arithmetical Compactness Theorem.
Mathematical Logic Quarterly,
Vol. 17,
Issue. 1,
p.
285.
Flum, Jörg
1971.
Ganzgeschlossene und prädikatengeschlossene Logiken I.
Archiv für Mathematische Logik und Grundlagenforschung,
Vol. 14,
Issue. 1-2,
p.
24.
GIEDYMIN, JERZY
1972.
QUINE'S PHILOSOPHICAL NATURALISM.
The British Journal for the Philosophy of Science,
Vol. 23,
Issue. 1,
p.
45.
Sinks, John D.
1972.
Fictionalism and the Elimination of Theoretical Terms.
Philosophy of Science,
Vol. 39,
Issue. 3,
p.
285.
Cornman, James W.
1972.
Craig's theorem, Ramsey-sentences, and scientific instrumentalism.
Synthese,
Vol. 25,
Issue. 1-2,
p.
82.
Montague, Richard
1972.
Semantics of Natural Language.
p.
142.
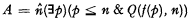 , where f is a primitive recursive function which enumerates B, has the required properties. For each m ϵ B, there is an n ϵ A, such that Q(m, n) and hence Q(n, m); therefore the closure of A under Q, and hence that under R, includes B. Conversely, since Q is a subrelation of R, A is included in C. Finally, that A is primitive recursive follows from [2] p. 180.
, where f is a primitive recursive function which enumerates B, has the required properties. For each m ϵ B, there is an n ϵ A, such that Q(m, n) and hence Q(n, m); therefore the closure of A under Q, and hence that under R, includes B. Conversely, since Q is a subrelation of R, A is included in C. Finally, that A is primitive recursive follows from [2] p. 180.
