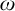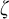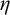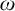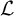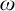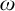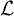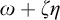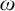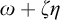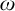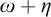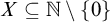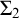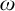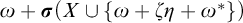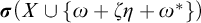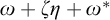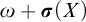1 Introduction
The ultimate inspiration for this work is Skolem’s 1934 construction of a countable non-standard model of arithmetic [Reference Skolem22]. Skolem’s construction can be described roughly as follows. For sets
![]() $X, Y \subseteq \mathbb {N}$
, write
$X, Y \subseteq \mathbb {N}$
, write
![]() $X \subseteq ^* Y$
if
$X \subseteq ^* Y$
if
![]() $X \setminus Y$
is finite. First, fix an infinite set
$X \setminus Y$
is finite. First, fix an infinite set
![]() $C \subseteq \mathbb {N}$
that is cohesive for the collection of arithmetical sets: for every arithmetical
$C \subseteq \mathbb {N}$
that is cohesive for the collection of arithmetical sets: for every arithmetical
![]() $A \subseteq \mathbb {N}$
, either
$A \subseteq \mathbb {N}$
, either
![]() $C \subseteq ^* A$
or
$C \subseteq ^* A$
or
![]() $C \subseteq ^* \overline {A}$
. Next, define an equivalence relation
$C \subseteq ^* \overline {A}$
. Next, define an equivalence relation
![]() $=_C$
on the arithmetical functions
$=_C$
on the arithmetical functions
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
by
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
by
![]() $f =_C g$
if and only if
$f =_C g$
if and only if
![]() $C \subseteq ^* \{n : f(n) = g(n)\}$
. Then define a structure on the
$C \subseteq ^* \{n : f(n) = g(n)\}$
. Then define a structure on the
![]() $=_C$
-equivalence classes
$=_C$
-equivalence classes
![]() $[f]$
by
$[f]$
by
![]() $[f] + [g] = [f + g]$
,
$[f] + [g] = [f + g]$
,
![]() $[f] \times [g] = [f \times g]$
(where
$[f] \times [g] = [f \times g]$
(where
![]() $f + g$
and
$f + g$
and
![]() $f \times g$
are computed pointwise), and
$f \times g$
are computed pointwise), and
![]() $[f] < [g] \;\Leftrightarrow \; C \subseteq ^* \{n : f(n) < g(n)\}$
. Using the arithmetical cohesiveness of C, one then shows that this structure is elementarily equivalent to
$[f] < [g] \;\Leftrightarrow \; C \subseteq ^* \{n : f(n) < g(n)\}$
. Using the arithmetical cohesiveness of C, one then shows that this structure is elementarily equivalent to
![]() $(\mathbb {N}, +, \times , <)$
. The structure is countable because there are only countably many arithmetical functions, and it has non-standard elements, such as the element represented by the identity function. See [Reference Dimitrov, Harizanov and Sriraman6] for a further discussion of Skolem’s model.
$(\mathbb {N}, +, \times , <)$
. The structure is countable because there are only countably many arithmetical functions, and it has non-standard elements, such as the element represented by the identity function. See [Reference Dimitrov, Harizanov and Sriraman6] for a further discussion of Skolem’s model.
Think of Skolem’s construction as a more effective analog of an ultrapower construction. Instead of building a structure from all functions
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
, Skolem builds a structure from only the arithmetical functions f. The arithmetically cohesive set C plays the role of the ultrafilter. Feferman, Scott, and Tennenbaum [Reference Feferman, Scott and Tennenbaum10] investigate the question of whether Skolem’s construction can be made more effective by assuming that C is only r-cohesive (i.e., cohesive for the collection of computable sets) and by restricting to computable functions f. They answer the question negatively by showing that it is not even possible to obtain a model of Peano arithmetic in this way. Lerman [Reference Lerman16] investigates the situation further and shows that if one restricts to cohesive sets C (i.e., cohesive for the collection of c.e. sets) that are co-c.e. and to computable functions f, then the first-order theory of the structure obtained is exactly determined by the many-one degree of C. Additional results in this direction appear in [Reference Hirschfeld12, Reference Hirschfeld and Wheeler13].
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
, Skolem builds a structure from only the arithmetical functions f. The arithmetically cohesive set C plays the role of the ultrafilter. Feferman, Scott, and Tennenbaum [Reference Feferman, Scott and Tennenbaum10] investigate the question of whether Skolem’s construction can be made more effective by assuming that C is only r-cohesive (i.e., cohesive for the collection of computable sets) and by restricting to computable functions f. They answer the question negatively by showing that it is not even possible to obtain a model of Peano arithmetic in this way. Lerman [Reference Lerman16] investigates the situation further and shows that if one restricts to cohesive sets C (i.e., cohesive for the collection of c.e. sets) that are co-c.e. and to computable functions f, then the first-order theory of the structure obtained is exactly determined by the many-one degree of C. Additional results in this direction appear in [Reference Hirschfeld12, Reference Hirschfeld and Wheeler13].
Dimitrov [Reference Dimitrov4] generalizes the effective ultrapower construction to arbitrary computable structures. These cohesive powers of computable structures are studied in [Reference Dimitrov3, Reference Dimitrov and Harizanov5, Reference Dimitrov, Harizanov, Miller, Mourad, Beckmann, Csuhaj-Varjú and Meer8] in relation to the lattice of c.e. subspaces, modulo finite dimension, of a fixed computable infinite dimensional vector space over the field
![]() $\mathbb {Q}$
. In this work, we investigate a question dual to the question studied by Lerman. Lerman fixes a computable presentation of a computable structure (indeed, all computable presentations of the standard model of arithmetic are computably isomorphic) and studies the effect that the choice of the cohesive set has on the resulting cohesive power. Instead of fixing a computable presentation of a structure and varying the cohesive set, we fix a computably presentable structure and a cohesive set, and then we vary the structure’s computable presentation. We focus on linear orders, with special emphasis on computable presentations of
$\mathbb {Q}$
. In this work, we investigate a question dual to the question studied by Lerman. Lerman fixes a computable presentation of a computable structure (indeed, all computable presentations of the standard model of arithmetic are computably isomorphic) and studies the effect that the choice of the cohesive set has on the resulting cohesive power. Instead of fixing a computable presentation of a structure and varying the cohesive set, we fix a computably presentable structure and a cohesive set, and then we vary the structure’s computable presentation. We focus on linear orders, with special emphasis on computable presentations of
![]() $\omega $
. We choose to work with linear orders because they are a good source of non-computably categorical structures and because the setting is simple enough to be able to completely describe certain cohesive powers up to isomorphism. This work is a greatly expanded version of the preliminary work of [Reference Dimitrov, Harizanov, Morozov, Shafer, Soskova, Vatev, Manea, Martin, Paulusma and Primiero9].
$\omega $
. We choose to work with linear orders because they are a good source of non-computably categorical structures and because the setting is simple enough to be able to completely describe certain cohesive powers up to isomorphism. This work is a greatly expanded version of the preliminary work of [Reference Dimitrov, Harizanov, Morozov, Shafer, Soskova, Vatev, Manea, Martin, Paulusma and Primiero9].
Our main results are the following. Below,
![]() $\omega $
,
$\omega $
,
![]() $\zeta $
, and
$\zeta $
, and
![]() $\eta $
denote the respective order-types of the natural numbers, the integers, and the rationals. For each
$\eta $
denote the respective order-types of the natural numbers, the integers, and the rationals. For each
![]() $k \geq 1$
,
$k \geq 1$
,
![]() $\boldsymbol {k}$
denotes the order-type of the k-element linear order.
$\boldsymbol {k}$
denotes the order-type of the k-element linear order.
-
• If C is cohesive and
 $\mathcal {L}$
is a computable copy of
$\mathcal {L}$
is a computable copy of
 $\omega $
that is computably isomorphic to the usual presentation of
$\omega $
that is computably isomorphic to the usual presentation of
 $\omega $
(i.e., the immediate successor relation of
$\omega $
(i.e., the immediate successor relation of
 $\mathcal {L}$
is computable), then the cohesive power
$\mathcal {L}$
is computable), then the cohesive power
 $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
 $\omega + \zeta \eta $
(Theorem 4.5).
$\omega + \zeta \eta $
(Theorem 4.5). -
• If C is co-c.e. and cohesive and
 $\mathcal {L}$
is a computable copy of
$\mathcal {L}$
is a computable copy of
 $\omega $
, then the finite condensation of the cohesive power
$\omega $
, then the finite condensation of the cohesive power
 $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
 $\boldsymbol {1} + \eta $
(Theorem 4.4; see Definition 3.3 for the definition of finite condensation).
$\boldsymbol {1} + \eta $
(Theorem 4.4; see Definition 3.3 for the definition of finite condensation). -
• If C is co-c.e. and cohesive, then there is a computable copy
 $\mathcal {L}$
of
$\mathcal {L}$
of
 $\omega $
where the cohesive power
$\omega $
where the cohesive power
 $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
 $\omega + \eta $
(Corollary 5.4).
$\omega + \eta $
(Corollary 5.4). -
• More generally, if C is co-c.e. and cohesive and
 $X \subseteq \mathbb {N} \setminus \{0\}$
is a Boolean combination of
$X \subseteq \mathbb {N} \setminus \{0\}$
is a Boolean combination of
 $\Sigma _2$
sets, thought of as a set of finite order-types, then there is a computable copy
$\Sigma _2$
sets, thought of as a set of finite order-types, then there is a computable copy
 $\mathcal {L}$
of
$\mathcal {L}$
of
 $\omega $
where the cohesive power
$\omega $
where the cohesive power
 $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
 $\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. Here
$\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. Here
 $\omega ^*$
denotes the reverse of
$\omega ^*$
denotes the reverse of
 $\omega $
, and
$\omega $
, and
 $\boldsymbol {\sigma }$
denotes the shuffle operation of Definition 6.2. Furthermore, if X is finite and non-empty, then there is a computable copy
$\boldsymbol {\sigma }$
denotes the shuffle operation of Definition 6.2. Furthermore, if X is finite and non-empty, then there is a computable copy
 $\mathcal {L}$
of
$\mathcal {L}$
of
 $\omega $
where the cohesive power
$\omega $
where the cohesive power
 $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
 $\omega + \boldsymbol {\sigma }(X)$
(Theorem 6.10).
$\omega + \boldsymbol {\sigma }(X)$
(Theorem 6.10).
This work also serves to compare and contrast properties of cohesive powers with those of classical ultrapowers. The key points are the following. Recall that a computable structure is decidable if its elementary diagram is computable and is n-decidable if its
![]() $\Sigma _n$
-elementary diagram is computable. These definitions are discussed in more detail in Section 2.
$\Sigma _n$
-elementary diagram is computable. These definitions are discussed in more detail in Section 2.
-
• Classically, an ultrapower of a structure is elementarily equivalent to the base structure by Łoś’s theorem. Effectively, Łoś’s theorem holds for cohesive powers of decidable structures (Corollary 2.10). For cohesive powers of n-decidable structures, Łoś’s theorem need only hold up to
 $\Delta _{n+3}$
-expressible sentences. In fact, every
$\Delta _{n+3}$
-expressible sentences. In fact, every
 $\Sigma _{n+3}$
sentence true of an n-decidable structure is also true of all of its cohesive powers (Theorem 2.9), but this is optimal in general (Corollary 4.9).
$\Sigma _{n+3}$
sentence true of an n-decidable structure is also true of all of its cohesive powers (Theorem 2.9), but this is optimal in general (Corollary 4.9). -
• Classically, ultrapowers of isomorphic structures over a fixed ultrafilter are isomorphic. Effectively, cohesive powers of computably isomorphic computable structures over a fixed cohesive set are isomorphic (Theorem 2.20). However, it is possible for isomorphic (but not computably isomorphic) computable structures to have non-elementarily equivalent (hence non-isomorphic) cohesive powers over a fixed cohesive set. Together, Theorems 4.5 and 4.8 imply that for every cohesive set C, there are computable copies
 $\mathcal {L}_0$
and
$\mathcal {L}_0$
and
 $\mathcal {L}_1$
of
$\mathcal {L}_1$
of
 $\omega $
such that the cohesive powers
$\omega $
such that the cohesive powers
 $\prod _C \mathcal {L}_0$
and
$\prod _C \mathcal {L}_0$
and
 $\prod _C \mathcal {L}_1$
are not elementarily equivalent. This sort of phenomenon can also be witnessed by computable structures whose cohesive powers are completely described. Fix a co-c.e. cohesive set. Example 5.5 shows that for every
$\prod _C \mathcal {L}_1$
are not elementarily equivalent. This sort of phenomenon can also be witnessed by computable structures whose cohesive powers are completely described. Fix a co-c.e. cohesive set. Example 5.5 shows that for every
 $k \geq 1$
, there is a computable copy
$k \geq 1$
, there is a computable copy
 $\mathcal {L}$
of
$\mathcal {L}$
of
 $\omega $
with
$\omega $
with
 $\prod _C \mathcal {L} \;\cong \; \omega + \boldsymbol {k}\eta $
. The order-types
$\prod _C \mathcal {L} \;\cong \; \omega + \boldsymbol {k}\eta $
. The order-types
 $\omega + \boldsymbol {k}\eta $
are pairwise non-elementarily equivalent for
$\omega + \boldsymbol {k}\eta $
are pairwise non-elementarily equivalent for
 $k \geq 1$
. Theorem 6.10 shows that many more order-types are achievable as cohesive powers of computable copies of
$k \geq 1$
. Theorem 6.10 shows that many more order-types are achievable as cohesive powers of computable copies of
 $\omega $
.
$\omega $
. -
• Classically, the Keisler–Shelah theorem states that two structures are elementarily equivalent if and only if there is an ultrafilter (on a set of appropriate size) over which the corresponding ultrapowers are isomorphic. Effectively, an analogous result holds for decidable structures: decidable structures
 $\mathcal {A}$
and
$\mathcal {A}$
and
 $\mathcal {B}$
are elementarily equivalent if and only if
$\mathcal {B}$
are elementarily equivalent if and only if
 $\prod _C \mathcal {A} \;\cong \; \prod _C \mathcal {B}$
for every cohesive set C (Theorem 2.22, which is essentially due to Nelson [Reference Nelson20] in a slightly different context). If
$\prod _C \mathcal {A} \;\cong \; \prod _C \mathcal {B}$
for every cohesive set C (Theorem 2.22, which is essentially due to Nelson [Reference Nelson20] in a slightly different context). If
 $\mathcal {A}$
and
$\mathcal {A}$
and
 $\mathcal {B}$
are computable structures that are not necessarily decidable, then the effective version of the Keisler–Shelah theorem can fail in either direction. As explained in the previous bullet, there are many examples of elementarily equivalent computable linear orders having non-isomorphic cohesive powers. Example 5.5 also shows that it is possible for non-elementarily equivalent computable linear orders to have isomorphic cohesive powers.
$\mathcal {B}$
are computable structures that are not necessarily decidable, then the effective version of the Keisler–Shelah theorem can fail in either direction. As explained in the previous bullet, there are many examples of elementarily equivalent computable linear orders having non-isomorphic cohesive powers. Example 5.5 also shows that it is possible for non-elementarily equivalent computable linear orders to have isomorphic cohesive powers. -
• Classically, for a countable language, ultrapowers over countably incomplete ultrafilters (i.e., ultrafilters that are not closed under countable intersections) are always
 $\aleph _1$
-saturated. Effectively, cohesive powers of decidable structures are recursively saturated (Theorem 2.16 item (3), which is essentially due to Nelson [Reference Nelson20] in a slightly different context). Furthermore, for
$\aleph _1$
-saturated. Effectively, cohesive powers of decidable structures are recursively saturated (Theorem 2.16 item (3), which is essentially due to Nelson [Reference Nelson20] in a slightly different context). Furthermore, for
 $n> 0$
, cohesive powers of n-decidable structures are
$n> 0$
, cohesive powers of n-decidable structures are
 $\Sigma _n$
-recursively saturated (Theorem 2.16 item (4)). Most interestingly, if the cohesive set is assumed to be co-c.e., then we obtain the
$\Sigma _n$
-recursively saturated (Theorem 2.16 item (4)). Most interestingly, if the cohesive set is assumed to be co-c.e., then we obtain the
 $n=0$
case as well as an additional level of saturation: cohesive powers of n-decidable structures over co-c.e. cohesive sets are
$n=0$
case as well as an additional level of saturation: cohesive powers of n-decidable structures over co-c.e. cohesive sets are
 $\Sigma _{n+1}$
-recursively saturated (Theorem 2.18).
$\Sigma _{n+1}$
-recursively saturated (Theorem 2.18).
This work is organized as follows. Section 2 presents the basic theory of cohesive products and cohesive powers, focusing on analogs of Łoś’s theorem, substructures, saturation, and isomorphisms. Section 3 concerns the cohesive powers of computable linear orders in general. Section 4 concerns the cohesive powers of computable copies of
![]() $\omega $
. In Section 5, given a co-c.e. cohesive set C, we construct a computable copy
$\omega $
. In Section 5, given a co-c.e. cohesive set C, we construct a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
whose cohesive power
$\omega $
whose cohesive power
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \eta $
. Section 6 leverages the construction of Section 5 to shuffle various patterns of finite order-types into cohesive powers of computable copies of
$\omega + \eta $
. Section 6 leverages the construction of Section 5 to shuffle various patterns of finite order-types into cohesive powers of computable copies of
![]() $\omega $
.
$\omega $
.
2 Cohesive products and powers of computable structures
We assume familiarity with the basic concepts and notation from computability theory and computable structure theory. Comprehensive references include [Reference Lerman17, Reference Soare23, Reference Soare24] for computability theory and [Reference Ash and Knight1, Reference Montalbán18] for computable structure theory. See also [Reference Fokina, Harizanov, Melnikov and Downey11] for a survey of computable structure theory.
Throughout,
![]() $\mathbb {N}$
denotes the natural numbers, and
$\mathbb {N}$
denotes the natural numbers, and
![]() $\omega $
denotes its order-type when thought of as a linear order. For each
$\omega $
denotes its order-type when thought of as a linear order. For each
![]() $n \geq 2$
, we use
$n \geq 2$
, we use
![]() $\langle x_0, \dots , x_{n-1} \rangle \colon \mathbb {N}^n \rightarrow \mathbb {N}$
to denote the usual computable bijective n-tupling function, which we may assume is increasing in all coordinates. For each
$\langle x_0, \dots , x_{n-1} \rangle \colon \mathbb {N}^n \rightarrow \mathbb {N}$
to denote the usual computable bijective n-tupling function, which we may assume is increasing in all coordinates. For each
![]() $i < n$
,
$i < n$
,
![]() $\pi _i$
denotes the corresponding projection function onto coordinate i. For
$\pi _i$
denotes the corresponding projection function onto coordinate i. For
![]() $X \subseteq \mathbb {N}$
and
$X \subseteq \mathbb {N}$
and
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $X {\restriction } n$
denotes the set
$X {\restriction } n$
denotes the set
![]() $X \cap \{0, 1, \dots , n-1\}$
. Often we consider expressions of the form
$X \cap \{0, 1, \dots , n-1\}$
. Often we consider expressions of the form
![]() $\lim _{n \in C} f(n)$
,
$\lim _{n \in C} f(n)$
,
![]() $\limsup _{n \in C} f(n)$
,
$\limsup _{n \in C} f(n)$
,
![]() $\liminf _{n \in C} f(n)$
, etc., where
$\liminf _{n \in C} f(n)$
, etc., where
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
is some function and
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
is some function and
![]() $C \subseteq \mathbb {N}$
is an infinite set. For this, let
$C \subseteq \mathbb {N}$
is an infinite set. For this, let
![]() $n_0 < n_1 < n_2 < \ldots $
be the elements of C listed in increasing order. Then
$n_0 < n_1 < n_2 < \ldots $
be the elements of C listed in increasing order. Then
![]() $\lim _{n \in C} f(n)$
means
$\lim _{n \in C} f(n)$
means
![]() $\lim _{i \rightarrow \infty } f(n_i)$
, and
$\lim _{i \rightarrow \infty } f(n_i)$
, and
![]() $\limsup _{n \in C} f(n)$
and
$\limsup _{n \in C} f(n)$
and
![]() $\liminf _{n \in C} f(n)$
are interpreted similarly. Notice that for functions
$\liminf _{n \in C} f(n)$
are interpreted similarly. Notice that for functions
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
,
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
,
![]() $\lim _{n \in C} f(n) = \infty $
if and only if
$\lim _{n \in C} f(n) = \infty $
if and only if
![]() $\liminf _{n \in C} f(n) = \infty $
.
$\liminf _{n \in C} f(n) = \infty $
.
We denote partial computable functions by
![]() $\varphi $
,
$\varphi $
,
![]() $\psi $
, etc. For a partial computable function
$\psi $
, etc. For a partial computable function
![]() $\varphi $
,
$\varphi $
,
![]() $\varphi (n){\downarrow }$
means that
$\varphi (n){\downarrow }$
means that
![]() $\varphi $
halts on input n, thus producing an output, and
$\varphi $
halts on input n, thus producing an output, and
![]() $\varphi (n){\uparrow }$
means that
$\varphi (n){\uparrow }$
means that
![]() $\varphi $
does not halt on input n. The notation
$\varphi $
does not halt on input n. The notation
![]() $\varphi \simeq \psi $
means that
$\varphi \simeq \psi $
means that
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are equal partial functions: for every n, either
$\psi $
are equal partial functions: for every n, either
![]() $\varphi (n){\downarrow } = \psi (n){\downarrow }$
or both
$\varphi (n){\downarrow } = \psi (n){\downarrow }$
or both
![]() $\varphi (n){\uparrow }$
and
$\varphi (n){\uparrow }$
and
![]() $\psi (n){\uparrow }$
. We also use the
$\psi (n){\uparrow }$
. We also use the
![]() $\simeq $
notation to define one partial computable function in terms of another. For example, “let
$\simeq $
notation to define one partial computable function in terms of another. For example, “let
![]() $\varphi (n) \simeq \psi (n) + 1$
” means compute
$\varphi (n) \simeq \psi (n) + 1$
” means compute
![]() $\varphi (n)$
by running
$\varphi (n)$
by running
![]() $\psi (n)$
and adding
$\psi (n)$
and adding
![]() $1$
to the output if
$1$
to the output if
![]() $\psi (n)$
halts. As usual,
$\psi (n)$
halts. As usual,
![]() $(\varphi _e)_{e \in \mathbb {N}}$
denotes the standard effective enumeration of all partial computable functions, and
$(\varphi _e)_{e \in \mathbb {N}}$
denotes the standard effective enumeration of all partial computable functions, and
![]() $\varphi _{e,s}(n)$
denotes the result (if any) of running
$\varphi _{e,s}(n)$
denotes the result (if any) of running
![]() $\varphi _e$
on input n for s computational steps. Sometimes we also write
$\varphi _e$
on input n for s computational steps. Sometimes we also write
![]() $\varphi _0, \dots , \varphi _{n-1}$
to refer to an arbitrary list of partial computable functions. The usage of subscripts will be clear from context.
$\varphi _0, \dots , \varphi _{n-1}$
to refer to an arbitrary list of partial computable functions. The usage of subscripts will be clear from context.
Throughout, we consider only first-order languages
![]() $\mathfrak {L}$
and finite first-order
$\mathfrak {L}$
and finite first-order
![]() $\mathfrak {L}$
-formulas. For
$\mathfrak {L}$
-formulas. For
![]() $k \in \mathbb {N}$
, we sometimes use the abbreviation
$k \in \mathbb {N}$
, we sometimes use the abbreviation
![]() $\exists ^{\geq k} x\, \Phi (x)$
to express that there are at least k distinct x for which
$\exists ^{\geq k} x\, \Phi (x)$
to express that there are at least k distinct x for which
![]() $\Phi (x)$
holds
$\Phi (x)$
holds
 $$ \begin{align*} \exists^{\geq k} x\, \Phi(x) \quad\equiv\quad \exists x_0, \dots, x_{k-1} \, \left[\left(\bigwedge_{i < j < k}x_i \neq x_j\right) \;\wedge\; \left(\bigwedge_{i < k} \Phi(x_i)\right)\right]. \end{align*} $$
$$ \begin{align*} \exists^{\geq k} x\, \Phi(x) \quad\equiv\quad \exists x_0, \dots, x_{k-1} \, \left[\left(\bigwedge_{i < j < k}x_i \neq x_j\right) \;\wedge\; \left(\bigwedge_{i < k} \Phi(x_i)\right)\right]. \end{align*} $$
Similarly, we use the abbreviation
![]() $\exists ^{= k} x\, \Phi (x)$
to express that there are exactly k distinct x for which
$\exists ^{= k} x\, \Phi (x)$
to express that there are exactly k distinct x for which
![]() $\Phi (x)$
holds:
$\Phi (x)$
holds:
![]() $\exists ^{= k} x\, \Phi (x) \;\equiv \; \exists ^{\geq k} x\, \Phi (x) \;\wedge \; \neg \exists ^{\geq k+1} x\, \Phi (x)$
. We point out that, for example, if
$\exists ^{= k} x\, \Phi (x) \;\equiv \; \exists ^{\geq k} x\, \Phi (x) \;\wedge \; \neg \exists ^{\geq k+1} x\, \Phi (x)$
. We point out that, for example, if
![]() $\Phi (x)$
is a
$\Phi (x)$
is a
![]() $\Sigma _1$
formula, then
$\Sigma _1$
formula, then
![]() $\exists ^{\geq k} x\, \Phi (x)$
is equivalent to a
$\exists ^{\geq k} x\, \Phi (x)$
is equivalent to a
![]() $\Sigma _1$
formula and
$\Sigma _1$
formula and
![]() $\exists ^{= k} x\, \Phi (x)$
is equivalent to the conjunction of a
$\exists ^{= k} x\, \Phi (x)$
is equivalent to the conjunction of a
![]() $\Sigma _1$
formula and a
$\Sigma _1$
formula and a
![]() $\Pi _1$
formula. In a slight abuse of the terminology, we say that a formula is
$\Pi _1$
formula. In a slight abuse of the terminology, we say that a formula is
![]() $\Delta _n$
if it is logically equivalent to both a
$\Delta _n$
if it is logically equivalent to both a
![]() $\Sigma _n$
formula and a
$\Sigma _n$
formula and a
![]() $\Pi _n$
formula. So if
$\Pi _n$
formula. So if
![]() $\Phi (x)$
is
$\Phi (x)$
is
![]() $\Sigma _1$
, then
$\Sigma _1$
, then
![]() $\exists ^{= k} x\, \Phi (x)$
is
$\exists ^{= k} x\, \Phi (x)$
is
![]() $\Delta _2$
.
$\Delta _2$
.
Fix a computable language
![]() $\mathfrak {L}$
. A computable
$\mathfrak {L}$
. A computable
![]() $\mathfrak {L}$
-structure
$\mathfrak {L}$
-structure
![]() $\mathcal {A}$
consists of a non-empty computable domain
$\mathcal {A}$
consists of a non-empty computable domain
![]() $A \subseteq \mathbb {N}$
and a uniformly computable interpretation of all relation, function, and constant symbols of
$A \subseteq \mathbb {N}$
and a uniformly computable interpretation of all relation, function, and constant symbols of
![]() $\mathfrak {L}$
. We often denote the domain of a structure
$\mathfrak {L}$
. We often denote the domain of a structure
![]() $\mathcal {A}$
by
$\mathcal {A}$
by
![]() $|\mathcal {A}|$
. A computable
$|\mathcal {A}|$
. A computable
![]() $\mathfrak {L}$
-structure
$\mathfrak {L}$
-structure
![]() $\mathcal {A}$
is decidable if there is an algorithm which, given a formula
$\mathcal {A}$
is decidable if there is an algorithm which, given a formula
![]() $\Phi (x_0, \dots , x_{m-1})$
, with all free variables displayed, and a sequence of parameters
$\Phi (x_0, \dots , x_{m-1})$
, with all free variables displayed, and a sequence of parameters
![]() $\langle a_0, \dots , a_{m-1} \rangle $
each from
$\langle a_0, \dots , a_{m-1} \rangle $
each from
![]() $|\mathcal {A}|$
, determines whether or not
$|\mathcal {A}|$
, determines whether or not
![]() $\mathcal {A} \models \Phi (a_0, \dots , a_{m-1})$
. Likewise, a computable
$\mathcal {A} \models \Phi (a_0, \dots , a_{m-1})$
. Likewise, a computable
![]() $\mathfrak {L}$
-structure
$\mathfrak {L}$
-structure
![]() $\mathcal {A}$
is n-decidable if there is such an algorithm determining whether or not
$\mathcal {A}$
is n-decidable if there is such an algorithm determining whether or not
![]() $\Sigma _n$
formulas with parameters from
$\Sigma _n$
formulas with parameters from
![]() $|\mathcal {A}|$
hold in
$|\mathcal {A}|$
hold in
![]() $\mathcal {A}$
. In other words, a computable structure is a structure having a computable atomic diagram (or, equivalently, a computable quantifier-free diagram); a decidable structure is a structure having a computable elementary diagram; and an n-decidable structure is a structure having a computable
$\mathcal {A}$
. In other words, a computable structure is a structure having a computable atomic diagram (or, equivalently, a computable quantifier-free diagram); a decidable structure is a structure having a computable elementary diagram; and an n-decidable structure is a structure having a computable
![]() $\Sigma _n$
-elementary diagram. A
$\Sigma _n$
-elementary diagram. A
![]() $0$
-decidable structure is the same thing as a computable structure. Similarly, a sequence
$0$
-decidable structure is the same thing as a computable structure. Similarly, a sequence
![]() $(\mathcal {A}_i : i \in \mathbb {N})$
of
$(\mathcal {A}_i : i \in \mathbb {N})$
of
![]() $\mathfrak {L}$
-structures is uniformly computable, uniformly decidable, or uniformly n-decidable if the respective sequence of atomic, elementary, or
$\mathfrak {L}$
-structures is uniformly computable, uniformly decidable, or uniformly n-decidable if the respective sequence of atomic, elementary, or
![]() $\Sigma _n$
-elementary diagrams is uniformly computable.
$\Sigma _n$
-elementary diagrams is uniformly computable.
We find it convenient to extend the decidability terminology to individual formulas and to computable sequences of formulas that are not necessarily all members of some fixed syntactic class. Say that a computable sequence of formulas
![]() $(\Phi _i : i \in \mathbb {N})$
is uniformly decidable in a computable
$(\Phi _i : i \in \mathbb {N})$
is uniformly decidable in a computable
![]() $\mathfrak {L}$
-structure
$\mathfrak {L}$
-structure
![]() $\mathcal {A}$
if there is an algorithm that, given a subformula
$\mathcal {A}$
if there is an algorithm that, given a subformula
![]() $\Psi (\vec {y})$
of
$\Psi (\vec {y})$
of
![]() $\Phi _i$
for some i (including of course the possibility
$\Phi _i$
for some i (including of course the possibility
![]() $\Psi = \Phi _i$
) and an appropriate sequence of parameters
$\Psi = \Phi _i$
) and an appropriate sequence of parameters
![]() $\vec {a}$
from
$\vec {a}$
from
![]() $|\mathcal {A}|$
, determines whether or not
$|\mathcal {A}|$
, determines whether or not
![]() $\mathcal {A} \models \Psi (\vec {a})$
. The reason for including the decidability of subformulas is to permit inductive arguments and to ensure that we can effectively search for witnesses to existential quantifiers. These properties are used in the subsections on analogs of Łoś’s theorem and on saturation below, for example. Formally,
$\mathcal {A} \models \Psi (\vec {a})$
. The reason for including the decidability of subformulas is to permit inductive arguments and to ensure that we can effectively search for witnesses to existential quantifiers. These properties are used in the subsections on analogs of Łoś’s theorem and on saturation below, for example. Formally,
![]() $(\Phi _i : i \in \mathbb {N})$
is uniformly decidable in
$(\Phi _i : i \in \mathbb {N})$
is uniformly decidable in
![]() $\mathcal {A}$
if the set
$\mathcal {A}$
if the set
is computable. In the case of sequences of structures, say that a computable sequence of formulas
![]() $(\Phi _i : i \in \mathbb {N})$
is uniformly decidable in a computable sequence
$(\Phi _i : i \in \mathbb {N})$
is uniformly decidable in a computable sequence
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
of
$(\mathcal {A}_n : n \in \mathbb {N})$
of
![]() $\mathfrak {L}$
-structures if the set
$\mathfrak {L}$
-structures if the set
is computable. In the case of a single formula
![]() $\Phi $
(and its subformulas), we simply say that
$\Phi $
(and its subformulas), we simply say that
![]() $\Phi $
is decidable in a computable
$\Phi $
is decidable in a computable
![]() $\mathfrak {L}$
-structure
$\mathfrak {L}$
-structure
![]() $\mathcal {A}$
and that
$\mathcal {A}$
and that
![]() $\Phi $
is uniformly decidable in a uniformly computable sequence
$\Phi $
is uniformly decidable in a uniformly computable sequence
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
of
$(\mathcal {A}_n : n \in \mathbb {N})$
of
![]() $\mathfrak {L}$
-structures. In a decidable structure, every computable sequence of formulas is uniformly decidable. In an n-decidable structure, every computable sequence of
$\mathfrak {L}$
-structures. In a decidable structure, every computable sequence of formulas is uniformly decidable. In an n-decidable structure, every computable sequence of
![]() $\Sigma _n$
formulas (indeed, every computable sequence of Boolean combinations of
$\Sigma _n$
formulas (indeed, every computable sequence of Boolean combinations of
![]() $\Sigma _n$
formulas) is uniformly decidable.
$\Sigma _n$
formulas) is uniformly decidable.
2.1 Cohesive products and cohesive powers
Definition 2.1. An infinite set
![]() $C \subseteq \mathbb {N}$
is cohesive if for every c.e. set W, either
$C \subseteq \mathbb {N}$
is cohesive if for every c.e. set W, either
![]() $C \subseteq ^* W$
or
$C \subseteq ^* W$
or
![]() $C \subseteq ^* \overline {W}$
.
$C \subseteq ^* \overline {W}$
.
More generally, a straightforward induction shows that if C is a cohesive set and X is a Boolean combination of c.e. sets, then either
![]() $C \subseteq ^* X$
or
$C \subseteq ^* X$
or
![]() $C \subseteq ^* \overline {X}$
. Notice that if C is cohesive and X is a Boolean combination of c.e. sets, then
$C \subseteq ^* \overline {X}$
. Notice that if C is cohesive and X is a Boolean combination of c.e. sets, then
![]() $C \cap X$
being infinite implies that
$C \cap X$
being infinite implies that
![]() $C \subseteq ^* X$
. We use quantifiers
$C \subseteq ^* X$
. We use quantifiers
![]() $\forall ^\infty n$
and
$\forall ^\infty n$
and
![]() $\exists ^\infty n$
as abbreviations for “for almost every n” and “there are infinitely many n.” So, for example,
$\exists ^\infty n$
as abbreviations for “for almost every n” and “there are infinitely many n.” So, for example,
![]() $(\forall ^\infty n \in C)(n \in X)$
means
$(\forall ^\infty n \in C)(n \in X)$
means
![]() $C \subseteq ^* X$
.
$C \subseteq ^* X$
.
Definition 2.2. Let
![]() $\mathfrak {L}$
be a computable language. Let
$\mathfrak {L}$
be a computable language. Let
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
$(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
![]() $\mathfrak {L}$
-structures with corresponding uniformly computable sequence of non-empty domains
$\mathfrak {L}$
-structures with corresponding uniformly computable sequence of non-empty domains
![]() $(|\mathcal {A}_n| : n \in \mathbb {N})$
. Let
$(|\mathcal {A}_n| : n \in \mathbb {N})$
. Let
![]() $C \subseteq \mathbb {N}$
be cohesive. The cohesive product of
$C \subseteq \mathbb {N}$
be cohesive. The cohesive product of
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
over C is the
$(\mathcal {A}_n : n \in \mathbb {N})$
over C is the
![]() $\mathfrak {L}$
-structure
$\mathfrak {L}$
-structure
![]() $\prod _C \mathcal {A}_n$
defined as follows:
$\prod _C \mathcal {A}_n$
defined as follows:
-
• Let D be the set of partial computable functions
 $\varphi $
such that
$\varphi $
such that
 $\forall n \, (\varphi (n){\downarrow } \,\rightarrow \, \varphi (n) \in |\mathcal {A}_n|)$
and
$\forall n \, (\varphi (n){\downarrow } \,\rightarrow \, \varphi (n) \in |\mathcal {A}_n|)$
and
 $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
.
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
. -
• For
 $\varphi , \psi \in D$
, let
$\varphi , \psi \in D$
, let
 $\varphi =_C \psi $
denote
$\varphi =_C \psi $
denote
 $C \subseteq ^* \{n : \varphi (n){\downarrow } = \psi (n){\downarrow }\}$
. The relation
$C \subseteq ^* \{n : \varphi (n){\downarrow } = \psi (n){\downarrow }\}$
. The relation
 $=_C$
is an equivalence relation on D. Let
$=_C$
is an equivalence relation on D. Let
 $[\varphi ]$
denote the equivalence class of
$[\varphi ]$
denote the equivalence class of
 $\varphi \in D$
with respect to
$\varphi \in D$
with respect to
 $=_C$
.
$=_C$
. -
• The domain of
 $\prod _C \mathcal {A}_n$
is the set
$\prod _C \mathcal {A}_n$
is the set
 $|\prod _C \mathcal {A}_n| = \{[\varphi ] : \varphi \in D\}$
.
$|\prod _C \mathcal {A}_n| = \{[\varphi ] : \varphi \in D\}$
. -
• Let R be an m-ary relation symbol of
 $\mathfrak {L}$
. For
$\mathfrak {L}$
. For
 $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
, define
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
, define
 $R^{\prod _C \mathcal {A}_n}([\varphi _0], \dots , [\varphi _{m-1}])$
by Here we think of
$R^{\prod _C \mathcal {A}_n}([\varphi _0], \dots , [\varphi _{m-1}])$
by Here we think of $$ \begin{align*} R^{\prod_C \mathcal{A}_n}([\varphi_0], \dots, [\varphi_{m-1}]) \;\Leftrightarrow\; C \subseteq^* \bigl\{n : R^{\mathcal{A}_n}(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}. \end{align*} $$
$$ \begin{align*} R^{\prod_C \mathcal{A}_n}([\varphi_0], \dots, [\varphi_{m-1}]) \;\Leftrightarrow\; C \subseteq^* \bigl\{n : R^{\mathcal{A}_n}(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}. \end{align*} $$
 $R^{\mathcal {A}_n}(\varphi _0(n), \dots , \varphi _{m-1}(n))$
as including the condition that
$R^{\mathcal {A}_n}(\varphi _0(n), \dots , \varphi _{m-1}(n))$
as including the condition that
 $\varphi _i(n){\downarrow }$
for each
$\varphi _i(n){\downarrow }$
for each
 $i < m$
.
$i < m$
.
-
• Let f be an m-ary function symbol of
 $\mathfrak {L}$
. For
$\mathfrak {L}$
. For
 $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
, let
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
, let
 $\psi $
be the partial computable function defined by and notice that
$\psi $
be the partial computable function defined by and notice that $$ \begin{align*} \psi(n) \simeq f^{\mathcal{A}_n}(\varphi_0(n), \dots, \varphi_{m-1}(n)), \end{align*} $$
$$ \begin{align*} \psi(n) \simeq f^{\mathcal{A}_n}(\varphi_0(n), \dots, \varphi_{m-1}(n)), \end{align*} $$
 $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\psi )$
because
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\psi )$
because
 $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi _i)$
for each
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi _i)$
for each
 $i < m$
. Define
$i < m$
. Define
 $f^{\prod _C \mathcal {A}_n}$
by
$f^{\prod _C \mathcal {A}_n}$
by  $$ \begin{align*} f^{\prod_C \mathcal{A}_n}([\varphi_0], \dots, [\varphi_{m-1}]) = [\psi]. \end{align*} $$
$$ \begin{align*} f^{\prod_C \mathcal{A}_n}([\varphi_0], \dots, [\varphi_{m-1}]) = [\psi]. \end{align*} $$
-
• Let c be a constant symbol of
 $\mathfrak {L}$
. Let
$\mathfrak {L}$
. Let
 $\psi $
be the total computable function defined by
$\psi $
be the total computable function defined by
 $\psi (n) = c^{\mathcal {A}_n}$
, and define
$\psi (n) = c^{\mathcal {A}_n}$
, and define
 $c^{\prod _C \mathcal {A}_n} = [\psi ]$
.
$c^{\prod _C \mathcal {A}_n} = [\psi ]$
.
In the case where
![]() $\mathcal {A}_n$
is the same fixed computable structure
$\mathcal {A}_n$
is the same fixed computable structure
![]() $\mathcal {A}$
for every n, the cohesive product
$\mathcal {A}$
for every n, the cohesive product
![]() $\prod _C \mathcal {A}_n$
is called the cohesive power of
$\prod _C \mathcal {A}_n$
is called the cohesive power of
![]() $\mathcal {A}$
over C and is denoted
$\mathcal {A}$
over C and is denoted
![]() $\prod _C \mathcal {A}$
.
$\prod _C \mathcal {A}$
.
In Definition 2.2, it is equivalent to relax the condition
![]() $\forall n \, (\varphi (n){\downarrow } \,\rightarrow \, \varphi (n) \in |\mathcal {A}_n|)$
and
$\forall n \, (\varphi (n){\downarrow } \,\rightarrow \, \varphi (n) \in |\mathcal {A}_n|)$
and
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
of the first bullet to
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
of the first bullet to
![]() $(\forall ^\infty n \in C)(\varphi (n){\downarrow } \,\wedge \, \varphi (n) \in |\mathcal {A}_n|)$
. If
$(\forall ^\infty n \in C)(\varphi (n){\downarrow } \,\wedge \, \varphi (n) \in |\mathcal {A}_n|)$
. If
![]() $\varphi $
is a partial computable function satisfying the relaxed condition, let
$\varphi $
is a partial computable function satisfying the relaxed condition, let
![]() $\psi $
be the partial computable function given by
$\psi $
be the partial computable function given by
 $$ \begin{align*} \psi(n) = \begin{cases} \varphi(n), & \text{if }\varphi(n){\downarrow}\text{ and }\varphi(n) \in |\mathcal{A}_n|,\\ {\uparrow}, & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \psi(n) = \begin{cases} \varphi(n), & \text{if }\varphi(n){\downarrow}\text{ and }\varphi(n) \in |\mathcal{A}_n|,\\ {\uparrow}, & \text{otherwise}. \end{cases} \end{align*} $$
Then
![]() $\psi $
satisfies the original condition, and
$\psi $
satisfies the original condition, and
![]() $\psi =_C \varphi $
.
$\psi =_C \varphi $
.
We often consider cohesive powers of computable structures by co-c.e. cohesive sets. The co-c.e. cohesive sets are exactly the complements of the maximal sets, which are the co-atoms of the lattice of c.e. sets modulo finite difference (see [Reference Soare23, Section X.3]). Such sets exist by a well-known theorem of Friedberg (see [Reference Soare23, Theorem X.3.3]). Cohesive powers are intended to be effective analogs of ultrapowers, so in light of this analogy, it makes sense to impose effectivity on the cohesive set, which plays the role of the ultrafilter, as well as on the base structure itself. Technically, it helps to be able to learn what numbers are not in the cohesive set C when building a computable structure
![]() $\mathcal {A}$
so as to influence
$\mathcal {A}$
so as to influence
![]() $\prod _C \mathcal {A}$
in a particular way. Cohesive products by co-c.e. cohesive sets also have the helpful property that every member of the cohesive product has a total computable representative. Let
$\prod _C \mathcal {A}$
in a particular way. Cohesive products by co-c.e. cohesive sets also have the helpful property that every member of the cohesive product has a total computable representative. Let
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of structures with non-empty domain
$(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of structures with non-empty domain
![]() $|\mathcal {A}_n|$
for each n, and let
$|\mathcal {A}_n|$
for each n, and let
![]() $a_n$
be the first element of
$a_n$
be the first element of
![]() $|\mathcal {A}_n|$
for each n. Suppose that C is co-c.e. and cohesive, and let
$|\mathcal {A}_n|$
for each n. Suppose that C is co-c.e. and cohesive, and let
![]() $\varphi \colon \mathbb {N} \rightarrow \mathbb {N}$
be a partial computable function representing an element
$\varphi \colon \mathbb {N} \rightarrow \mathbb {N}$
be a partial computable function representing an element
![]() $[\varphi ]$
of
$[\varphi ]$
of
![]() $\prod _C \mathcal {A}_n$
. Then
$\prod _C \mathcal {A}_n$
. Then
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
, so let N be such that
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
, so let N be such that
![]() $(\forall n> N)(n \in C \rightarrow \varphi (n){\downarrow })$
. Define a total computable
$(\forall n> N)(n \in C \rightarrow \varphi (n){\downarrow })$
. Define a total computable
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
as follows. If
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
as follows. If
![]() $n \leq N$
, then output
$n \leq N$
, then output
![]() $f(n) = a_n$
. If
$f(n) = a_n$
. If
![]() $n> N$
, then simultaneously run
$n> N$
, then simultaneously run
![]() $\varphi (n)$
and enumerate the complement
$\varphi (n)$
and enumerate the complement
![]() $\overline {C}$
of C. Either
$\overline {C}$
of C. Either
![]() $\varphi (n){\downarrow }$
,
$\varphi (n){\downarrow }$
,
![]() $n \in \overline {C}$
, or both. If
$n \in \overline {C}$
, or both. If
![]() $\varphi (n)$
halts before n is enumerated into
$\varphi (n)$
halts before n is enumerated into
![]() $\overline {C}$
, then output
$\overline {C}$
, then output
![]() $f(n) = \varphi (n)$
; and if n is enumerated into
$f(n) = \varphi (n)$
; and if n is enumerated into
![]() $\overline {C}$
before
$\overline {C}$
before
![]() $\varphi (n)$
halts, then output
$\varphi (n)$
halts, then output
![]() $f(n) = a_n$
. This f is total and satisfies
$f(n) = a_n$
. This f is total and satisfies
![]() $f =_C \varphi $
.
$f =_C \varphi $
.
As with structures and their ultrapowers, a computable structure
![]() $\mathcal {A}$
always naturally embeds into its cohesive powers. For
$\mathcal {A}$
always naturally embeds into its cohesive powers. For
![]() $a \in |\mathcal {A}|$
, let
$a \in |\mathcal {A}|$
, let
![]() $f_a$
be the total computable function with constant value a. Then for any cohesive set C, the map
$f_a$
be the total computable function with constant value a. Then for any cohesive set C, the map
![]() $a \mapsto [f_a]$
embeds
$a \mapsto [f_a]$
embeds
![]() $\mathcal {A}$
into
$\mathcal {A}$
into
![]() $\prod _C \mathcal {A}$
. This map is called the canonical embedding of
$\prod _C \mathcal {A}$
. This map is called the canonical embedding of
![]() $\mathcal {A}$
into
$\mathcal {A}$
into
![]() $\prod _C \mathcal {A}$
. If
$\prod _C \mathcal {A}$
. If
![]() $\mathcal {A}$
is finite and C is cohesive, then every partial computable function
$\mathcal {A}$
is finite and C is cohesive, then every partial computable function
![]() $\varphi \colon \mathbb {N} \rightarrow |\mathcal {A}|$
with
$\varphi \colon \mathbb {N} \rightarrow |\mathcal {A}|$
with
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
is eventually constant on C. In this case, every element of
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
is eventually constant on C. In this case, every element of
![]() $\prod _C \mathcal {A}$
is in the range of the canonical embedding, and therefore
$\prod _C \mathcal {A}$
is in the range of the canonical embedding, and therefore
![]() $\mathcal {A} \cong \prod _C \mathcal {A}$
. If
$\mathcal {A} \cong \prod _C \mathcal {A}$
. If
![]() $\mathcal {A}$
is an infinite computable structure, then every cohesive power
$\mathcal {A}$
is an infinite computable structure, then every cohesive power
![]() $\prod _C \mathcal {A}$
is countably infinite: infinite because
$\prod _C \mathcal {A}$
is countably infinite: infinite because
![]() $\mathcal {A}$
embeds into
$\mathcal {A}$
embeds into
![]() $\prod _C \mathcal {A}$
, and countable because the elements of
$\prod _C \mathcal {A}$
, and countable because the elements of
![]() $\prod _C \mathcal {A}$
are represented by partial computable functions. See [Reference Dimitrov4] for further details.
$\prod _C \mathcal {A}$
are represented by partial computable functions. See [Reference Dimitrov4] for further details.
2.2 Analogs of Łoś’s theorem
A restricted form of Łoś’s theorem holds for cohesive powers. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $\mathcal {A}$
be an n-decidable
$\mathcal {A}$
be an n-decidable
![]() $\mathfrak {L}$
-structure, and let C be cohesive. We show that for every
$\mathfrak {L}$
-structure, and let C be cohesive. We show that for every
![]() $\Sigma _{n+3}$
sentence
$\Sigma _{n+3}$
sentence
![]() $\Phi $
,
$\Phi $
,
![]() $\mathcal {A} \models \Phi $
implies that
$\mathcal {A} \models \Phi $
implies that
![]() $\prod _C \mathcal {A} \models \Phi $
. It follows that
$\prod _C \mathcal {A} \models \Phi $
. It follows that
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\prod _C \mathcal {A}$
agree on all
$\prod _C \mathcal {A}$
agree on all
![]() $\Delta _{n+3}$
sentences. It also follows that if
$\Delta _{n+3}$
sentences. It also follows that if
![]() $\mathcal {A}$
is decidable, then
$\mathcal {A}$
is decidable, then
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\prod _C \mathcal {A}$
are elementarily equivalent. Thus for decidable structures, we recover the full Łoś theorem (for first-order logic). These results update Dimitrov’s fundamental theorem of cohesive powers [Reference Dimitrov4], which is the
$\prod _C \mathcal {A}$
are elementarily equivalent. Thus for decidable structures, we recover the full Łoś theorem (for first-order logic). These results update Dimitrov’s fundamental theorem of cohesive powers [Reference Dimitrov4], which is the
![]() $0$
-decidable case: if
$0$
-decidable case: if
![]() $\mathcal {A}$
is a computable
$\mathcal {A}$
is a computable
![]() $\mathfrak {L}$
-structure, C is cohesive, and
$\mathfrak {L}$
-structure, C is cohesive, and
![]() $\Phi $
is a
$\Phi $
is a
![]() $\Sigma _3$
sentence, then
$\Sigma _3$
sentence, then
![]() $\mathcal {A} \models \Phi $
implies that
$\mathcal {A} \models \Phi $
implies that
![]() $\prod _C \mathcal {A} \models \Phi $
. In general, the fundamental theorem of cohesive powers is the best possible analog of Łoś’s theorem. In Sections 4–6, we see several examples of computable linear orders
$\prod _C \mathcal {A} \models \Phi $
. In general, the fundamental theorem of cohesive powers is the best possible analog of Łoś’s theorem. In Sections 4–6, we see several examples of computable linear orders
![]() $\mathcal {L}$
where the
$\mathcal {L}$
where the
![]() $\Pi _3$
sentence “every element has an immediate successor” is true of
$\Pi _3$
sentence “every element has an immediate successor” is true of
![]() $\mathcal {L}$
but false of some cohesive power of
$\mathcal {L}$
but false of some cohesive power of
![]() $\mathcal {L}$
. For sequences of structures, we show that if
$\mathcal {L}$
. For sequences of structures, we show that if
![]() $(\mathcal {A}_i : i \in \mathbb {N})$
is a sequence of uniformly n-decidable
$(\mathcal {A}_i : i \in \mathbb {N})$
is a sequence of uniformly n-decidable
![]() $\mathfrak {L}$
-structures, C is cohesive, and
$\mathfrak {L}$
-structures, C is cohesive, and
![]() $\Phi $
is a
$\Phi $
is a
![]() $\Pi _{n+2}$
sentence, then
$\Pi _{n+2}$
sentence, then
![]() $C \subseteq ^* \bigl \{i : \mathcal {A}_i \models \Phi \bigr \}$
implies that
$C \subseteq ^* \bigl \{i : \mathcal {A}_i \models \Phi \bigr \}$
implies that
![]() $\prod _C \mathcal {A}_i \models \Phi $
. This updates the fundamental theorem of cohesive products from [Reference Dimitrov and Harizanov7], which is the
$\prod _C \mathcal {A}_i \models \Phi $
. This updates the fundamental theorem of cohesive products from [Reference Dimitrov and Harizanov7], which is the
![]() $0$
-decidable case. In Section 4, we show that the fundamental theorem of cohesive products is best possible by uniformly computing a sequence of finite linear orders
$0$
-decidable case. In Section 4, we show that the fundamental theorem of cohesive products is best possible by uniformly computing a sequence of finite linear orders
![]() $(\mathcal {L}_i : i \in \mathbb {N})$
such that for every cohesive set C, the cohesive product
$(\mathcal {L}_i : i \in \mathbb {N})$
such that for every cohesive set C, the cohesive product
![]() $\prod _C \mathcal {L}_i$
is a linear order with no maximum element.
$\prod _C \mathcal {L}_i$
is a linear order with no maximum element.
Lemma 2.3. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
$(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
![]() $\mathfrak {L}$
-structures, and let C be cohesive. Let
$\mathfrak {L}$
-structures, and let C be cohesive. Let
![]() $t(v_0, \dots , v_{m-1})$
be a term, with all variables displayed. Let
$t(v_0, \dots , v_{m-1})$
be a term, with all variables displayed. Let
![]() $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
. Let
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
. Let
![]() $\psi $
be the partial computable function given by
$\psi $
be the partial computable function given by
Then
Proof The proof is a straightforward induction on the construction of the term t, using Definition 2.2.
Lemma 2.4. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
$(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
![]() $\mathfrak {L}$
-structures, and let C be cohesive. Let
$\mathfrak {L}$
-structures, and let C be cohesive. Let
![]() $\Phi (v_0, \dots , v_{m-1})$
be a formula
$\Phi (v_0, \dots , v_{m-1})$
be a formula
![]() $($
with all free variables displayed
$($
with all free variables displayed
![]() $)$
that is uniformly decidable in
$)$
that is uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
. Then for any
$(\mathcal {A}_n : n \in \mathbb {N})$
. Then for any
![]() $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
,
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
,
Proof Proceed by induction on the construction of the formula
![]() $\Phi $
. For the base case, assume that
$\Phi $
. For the base case, assume that
![]() $\Phi (v_0, \dots , v_{m-1})$
is the atomic formula
$\Phi (v_0, \dots , v_{m-1})$
is the atomic formula
![]() $R\bigl (t_0(v_0, \dots , v_{m-1}), \dots , t_{\ell -1}(v_0, \dots , v_{m-1})\bigr )$
, where R is either a relation symbol from
$R\bigl (t_0(v_0, \dots , v_{m-1}), \dots , t_{\ell -1}(v_0, \dots , v_{m-1})\bigr )$
, where R is either a relation symbol from
![]() $\mathfrak {L}$
or equality, and
$\mathfrak {L}$
or equality, and
![]() $t_0, \dots , t_{\ell -1}$
are terms whose variables are among
$t_0, \dots , t_{\ell -1}$
are terms whose variables are among
![]() $v_0, \dots , v_{m-1}$
. For each
$v_0, \dots , v_{m-1}$
. For each
![]() $i < \ell $
, define
$i < \ell $
, define
as in Lemma 2.3 so that
![]() $t_i^{\prod _C \mathcal {A}_n}([\varphi _0], \dots , [\varphi _{m-1}]) = [\psi _i]$
. Then
$t_i^{\prod _C \mathcal {A}_n}([\varphi _0], \dots , [\varphi _{m-1}]) = [\psi _i]$
. Then
 $$ \begin{align*} && \prod\nolimits_C \mathcal{A}_n &\models R\bigl(t_0([\varphi_0], \dots, [\varphi_{m-1}]), \dots, t_{\ell-1}([\varphi_0], \dots, [\varphi_{m-1}])\bigr)\\ &\Leftrightarrow& \prod\nolimits_C \mathcal{A}_n &\models R([\psi_0], \dots, [\psi_{\ell-1}])\\ &\Leftrightarrow& C &\subseteq^* \bigl\{n : \mathcal{A}_n \models R(\psi_0(n), \dots, \psi_{\ell-1}(n))\bigr\}\\ &\Leftrightarrow& C &\subseteq^* \bigl\{n : \mathcal{A}_n \models R\bigl(t_0(\varphi_0(n), \dots, \varphi_{m-1}(n)), \dots, t_{\ell-1}(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr)\bigr\}. \end{align*} $$
$$ \begin{align*} && \prod\nolimits_C \mathcal{A}_n &\models R\bigl(t_0([\varphi_0], \dots, [\varphi_{m-1}]), \dots, t_{\ell-1}([\varphi_0], \dots, [\varphi_{m-1}])\bigr)\\ &\Leftrightarrow& \prod\nolimits_C \mathcal{A}_n &\models R([\psi_0], \dots, [\psi_{\ell-1}])\\ &\Leftrightarrow& C &\subseteq^* \bigl\{n : \mathcal{A}_n \models R(\psi_0(n), \dots, \psi_{\ell-1}(n))\bigr\}\\ &\Leftrightarrow& C &\subseteq^* \bigl\{n : \mathcal{A}_n \models R\bigl(t_0(\varphi_0(n), \dots, \varphi_{m-1}(n)), \dots, t_{\ell-1}(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr)\bigr\}. \end{align*} $$
We consider the inductive cases for the connectives
![]() $\wedge $
and
$\wedge $
and
![]() $\neg $
and for the quantifier
$\neg $
and for the quantifier
![]() $\exists $
.
$\exists $
.
Assume that
![]() $\Phi (v_0, \dots , v_{m-1})$
is the formula
$\Phi (v_0, \dots , v_{m-1})$
is the formula
![]() $\Phi _0(v_0, \dots , v_{m-1}) \wedge \Phi _1(v_0, \dots , v_{m-1})$
. Then
$\Phi _0(v_0, \dots , v_{m-1}) \wedge \Phi _1(v_0, \dots , v_{m-1})$
. Then
![]() $\prod _C \mathcal {A}_n \models \Phi ([\varphi _0], \dots , [\varphi _{m-1}])$
if and only if
$\prod _C \mathcal {A}_n \models \Phi ([\varphi _0], \dots , [\varphi _{m-1}])$
if and only if
![]() $(\forall i < 2) \bigl (\prod _C \mathcal {A}_n \models \Phi _i([\varphi _0], \dots , [\varphi _{m-1}])\bigr )$
. Formulas
$(\forall i < 2) \bigl (\prod _C \mathcal {A}_n \models \Phi _i([\varphi _0], \dots , [\varphi _{m-1}])\bigr )$
. Formulas
![]() $\Phi _0$
and
$\Phi _0$
and
![]() $\Phi _1$
are uniformly decidable in
$\Phi _1$
are uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
because they are subformulas of
$(\mathcal {A}_n : n \in \mathbb {N})$
because they are subformulas of
![]() $\Phi $
. Thus the induction hypothesis yields that
$\Phi $
. Thus the induction hypothesis yields that
for each
![]() $i < 2$
. Finally,
$i < 2$
. Finally,
![]() $C \subseteq ^* \bigl \{n : \mathcal {A}_n \models \Phi _i(\varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
holds for both
$C \subseteq ^* \bigl \{n : \mathcal {A}_n \models \Phi _i(\varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
holds for both
![]() $i=0$
and
$i=0$
and
![]() $i=1$
if and only if
$i=1$
if and only if
Putting this all together yields that
if and only if
Now assume that
![]() $\Phi (v_0, \dots , v_{m-1})$
is the formula
$\Phi (v_0, \dots , v_{m-1})$
is the formula
![]() $\neg \Psi (v_0, \dots , v_{m-1})$
. Then
$\neg \Psi (v_0, \dots , v_{m-1})$
. Then
![]() $\prod _C \mathcal {A}_n \models \Phi ([\varphi _0], \dots , [\varphi _{m-1}])$
if and only if
$\prod _C \mathcal {A}_n \models \Phi ([\varphi _0], \dots , [\varphi _{m-1}])$
if and only if
![]() $\prod _C \mathcal {A}_n \not \models \Psi ([\varphi _0], \dots , [\varphi _{m-1}])$
. The formula
$\prod _C \mathcal {A}_n \not \models \Psi ([\varphi _0], \dots , [\varphi _{m-1}])$
. The formula
![]() $\Psi $
is uniformly decidable in
$\Psi $
is uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
because it is a subformula of
$(\mathcal {A}_n : n \in \mathbb {N})$
because it is a subformula of
![]() $\Phi $
. Thus the induction hypothesis yields that
$\Phi $
. Thus the induction hypothesis yields that
We have that
![]() $C \nsubseteq ^* \bigl \{n : \mathcal {A}_n \models \Psi (\varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
if and only if C has infinite intersection with the set
$C \nsubseteq ^* \bigl \{n : \mathcal {A}_n \models \Psi (\varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
if and only if C has infinite intersection with the set
![]() $\bigl \{n : \mathcal {A}_n \not \models \Psi (\varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
, which is co-c.e. because
$\bigl \{n : \mathcal {A}_n \not \models \Psi (\varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
, which is co-c.e. because
![]() $\Psi (v_0, \dots , v_{m-1})$
is uniformly decidable in
$\Psi (v_0, \dots , v_{m-1})$
is uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
. By cohesiveness and the fact that
$(\mathcal {A}_n : n \in \mathbb {N})$
. By cohesiveness and the fact that
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi _i)$
for each
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi _i)$
for each
![]() $i < m$
, we therefore have that
$i < m$
, we therefore have that
 $$ \begin{align*} C \nsubseteq^* \bigl\{n : \mathcal{A}_n \models \Psi(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\} \quad&\Leftrightarrow\quad C \subseteq^* \bigl\{n : \mathcal{A}_n \not\models \Psi(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}\\ \quad&\Leftrightarrow\quad C \subseteq^* \bigl\{n : \mathcal{A}_n \models \neg\Psi(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}. \end{align*} $$
$$ \begin{align*} C \nsubseteq^* \bigl\{n : \mathcal{A}_n \models \Psi(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\} \quad&\Leftrightarrow\quad C \subseteq^* \bigl\{n : \mathcal{A}_n \not\models \Psi(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}\\ \quad&\Leftrightarrow\quad C \subseteq^* \bigl\{n : \mathcal{A}_n \models \neg\Psi(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}. \end{align*} $$
Putting this all together yields that
Finally, assume that
![]() $\Phi (v_0, \dots , v_{m-1})$
is the formula
$\Phi (v_0, \dots , v_{m-1})$
is the formula
![]() $\exists x\, \Psi (x, v_0, \dots , v_{m-1})$
. First suppose that
$\exists x\, \Psi (x, v_0, \dots , v_{m-1})$
. First suppose that
![]() $\prod _C \mathcal {A}_n \models \exists x\, \Psi (x, [\varphi _0], \dots , [\varphi _{m-1}])$
. Then there is a
$\prod _C \mathcal {A}_n \models \exists x\, \Psi (x, [\varphi _0], \dots , [\varphi _{m-1}])$
. Then there is a
![]() $[\theta ] \in |\prod _C \mathcal {A}_n|$
such that
$[\theta ] \in |\prod _C \mathcal {A}_n|$
such that
![]() $\prod _C \mathcal {A}_n \models \Psi ([\theta ], [\varphi _0], \dots , [\varphi _{m-1}])$
. The formula
$\prod _C \mathcal {A}_n \models \Psi ([\theta ], [\varphi _0], \dots , [\varphi _{m-1}])$
. The formula
![]() $\Psi $
is uniformly decidable in
$\Psi $
is uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
because it is a subformula of
$(\mathcal {A}_n : n \in \mathbb {N})$
because it is a subformula of
![]() $\Phi $
. Thus the induction hypothesis yields that
$\Phi $
. Thus the induction hypothesis yields that
Clearly
so we have that
![]() $C \subseteq ^* \bigl \{n : \mathcal {A}_n \models \exists x\, \Psi (x, \varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
.
$C \subseteq ^* \bigl \{n : \mathcal {A}_n \models \exists x\, \Psi (x, \varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
.
Conversely, suppose that
![]() $C \subseteq ^* \bigl \{n : \mathcal {A}_n \models \exists x\, \Psi (x, \varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
. The formula
$C \subseteq ^* \bigl \{n : \mathcal {A}_n \models \exists x\, \Psi (x, \varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
. The formula
![]() $\Psi (x, v_0, \dots , v_{m-1})$
is uniformly decidable in
$\Psi (x, v_0, \dots , v_{m-1})$
is uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
, so we may define a partial computable function
$(\mathcal {A}_n : n \in \mathbb {N})$
, so we may define a partial computable function
![]() $\theta $
by
$\theta $
by
The assumption
![]() $C \subseteq ^* \bigl \{n : \mathcal {A}_n \models \exists x\, \Psi (x, \varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
implies that
$C \subseteq ^* \bigl \{n : \mathcal {A}_n \models \exists x\, \Psi (x, \varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
implies that
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
. We therefore have that
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
. We therefore have that
![]() $[\theta ] \in |\prod _C \mathcal {A}_n|$
and that
$[\theta ] \in |\prod _C \mathcal {A}_n|$
and that
The induction hypothesis then yields that
![]() $\prod _C \mathcal {A}_n \models \Psi ([\theta ], [\varphi _0], \dots , [\varphi _{m-1}])$
. Therefore
$\prod _C \mathcal {A}_n \models \Psi ([\theta ], [\varphi _0], \dots , [\varphi _{m-1}])$
. Therefore
![]() $\prod _C \mathcal {A}_n \models \exists x\, \Psi (x, [\varphi _0], \dots , [\varphi _{m-1}])$
. This completes the proof.
$\prod _C \mathcal {A}_n \models \exists x\, \Psi (x, [\varphi _0], \dots , [\varphi _{m-1}])$
. This completes the proof.
Lemma 2.5. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
$(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
![]() $\mathfrak {L}$
-structures, and let C be cohesive. Let
$\mathfrak {L}$
-structures, and let C be cohesive. Let
![]() $\Psi (x_0, \dots , x_{k-1}, y_0, \dots , y_{\ell -1}, v_0, \dots , v_{m-1})$
be a formula that is uniformly decidable in
$\Psi (x_0, \dots , x_{k-1}, y_0, \dots , y_{\ell -1}, v_0, \dots , v_{m-1})$
be a formula that is uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
.
$(\mathcal {A}_n : n \in \mathbb {N})$
.
-
(1) For any
 $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
,
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
,  $$ \begin{align*} \prod\nolimits_C \mathcal{A}_n \models \exists \vec{x}\, \forall \vec{y}\, \Psi(\vec{x}, &\vec{y}, [\varphi_0], \dots, [\varphi_{m-1}]) \quad\Rightarrow \\ & C \subseteq^* \bigl\{n : \mathcal{A}_n \models \exists \vec{x}\, \forall \vec{y}\, \Psi(\vec{x}, \vec{y}, \varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathcal{A}_n \models \exists \vec{x}\, \forall \vec{y}\, \Psi(\vec{x}, &\vec{y}, [\varphi_0], \dots, [\varphi_{m-1}]) \quad\Rightarrow \\ & C \subseteq^* \bigl\{n : \mathcal{A}_n \models \exists \vec{x}\, \forall \vec{y}\, \Psi(\vec{x}, \vec{y}, \varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}. \end{align*} $$
-
(2) For any
 $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
,
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
,  $$ \begin{align*} C \subseteq^* \bigl\{n : \mathcal{A}_n \models \forall \vec{x}\, \exists \vec{y}\, \Psi(\vec{x}, \vec{y}, &\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\} \quad\Rightarrow\\ &\prod\nolimits_C \mathcal{A}_n \models \forall \vec{x}\, \exists \vec{y}\, \Psi(\vec{x}, \vec{y}, [\varphi_0], \dots, [\varphi_{m-1}]). \end{align*} $$
$$ \begin{align*} C \subseteq^* \bigl\{n : \mathcal{A}_n \models \forall \vec{x}\, \exists \vec{y}\, \Psi(\vec{x}, \vec{y}, &\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\} \quad\Rightarrow\\ &\prod\nolimits_C \mathcal{A}_n \models \forall \vec{x}\, \exists \vec{y}\, \Psi(\vec{x}, \vec{y}, [\varphi_0], \dots, [\varphi_{m-1}]). \end{align*} $$
Proof For item (1), suppose that
![]() $\prod _C \mathcal {A}_n \models \exists \vec {x}\, \forall \vec {y}\, \Psi (\vec {x}, \vec {y}, [\varphi _0], \dots , [\varphi _{m-1}])$
. Let
$\prod _C \mathcal {A}_n \models \exists \vec {x}\, \forall \vec {y}\, \Psi (\vec {x}, \vec {y}, [\varphi _0], \dots , [\varphi _{m-1}])$
. Let
![]() $[\psi _0], \dots , [\psi _{k-1}] \in |\prod _C \mathcal {A}_n|$
be such that
$[\psi _0], \dots , [\psi _{k-1}] \in |\prod _C \mathcal {A}_n|$
be such that
The set
is a Boolean combination of c.e. sets, so by cohesiveness, either
![]() $C \subseteq ^* X$
or
$C \subseteq ^* X$
or
![]() $C \subseteq ^* \overline {X}$
. If
$C \subseteq ^* \overline {X}$
. If
![]() $C \subseteq ^* \overline {X}$
, then because
$C \subseteq ^* \overline {X}$
, then because
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi _i)$
for each
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi _i)$
for each
![]() $i < m$
and
$i < m$
and
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\psi _i)$
for each
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\psi _i)$
for each
![]() $i < k$
, we would have that
$i < k$
, we would have that
As
![]() $\Psi $
is uniformly decidable in
$\Psi $
is uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
, we could then argue as in the
$(\mathcal {A}_n : n \in \mathbb {N})$
, we could then argue as in the
![]() $\exists $
case of the proof of Lemma 2.4 and simultaneously define partial computable functions
$\exists $
case of the proof of Lemma 2.4 and simultaneously define partial computable functions
![]() $\theta _i$
for
$\theta _i$
for
![]() $i < \ell $
as follows. Given n, search for the first sequence
$i < \ell $
as follows. Given n, search for the first sequence
![]() $\langle a_0, \dots , a_{\ell -1} \rangle \in |\mathcal {A}_n|^\ell $
such that
$\langle a_0, \dots , a_{\ell -1} \rangle \in |\mathcal {A}_n|^\ell $
such that
and set
![]() $\theta _i(n) = a_i$
for each
$\theta _i(n) = a_i$
for each
![]() $i < \ell $
. Then
$i < \ell $
. Then
so
by Lemma 2.4, which contradicts (*). Thus we cannot have
![]() $C \subseteq ^* \overline {X}$
, so it must be that
$C \subseteq ^* \overline {X}$
, so it must be that
![]() $C \subseteq ^* X$
. Therefore
$C \subseteq ^* X$
. Therefore
 $$ \begin{align*} C &\subseteq^* \bigl\{n : \mathcal{A}_n \models \forall \vec{y}\, \Psi(\psi_0(n), \dots, \psi_{k-1}(n), \vec{y}, \varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\},\\ &\subseteq^{\phantom{*}} \bigl\{n : \mathcal{A}_n \models \exists \vec{x}\, \forall \vec{y}\, \Psi(\vec{x}, \vec{y}, \varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}, \end{align*} $$
$$ \begin{align*} C &\subseteq^* \bigl\{n : \mathcal{A}_n \models \forall \vec{y}\, \Psi(\psi_0(n), \dots, \psi_{k-1}(n), \vec{y}, \varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\},\\ &\subseteq^{\phantom{*}} \bigl\{n : \mathcal{A}_n \models \exists \vec{x}\, \forall \vec{y}\, \Psi(\vec{x}, \vec{y}, \varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}, \end{align*} $$
as desired.
Item (2) follows from item (1). Suppose that
![]() $\prod _C \mathcal {A}_n \not \models \forall \vec {x}\, \exists \vec {y}\, \Psi (\vec {x}, \vec {y}, [\varphi _0], \dots , [\varphi _{m-1}])$
. Then
$\prod _C \mathcal {A}_n \not \models \forall \vec {x}\, \exists \vec {y}\, \Psi (\vec {x}, \vec {y}, [\varphi _0], \dots , [\varphi _{m-1}])$
. Then
![]() $\prod _C \mathcal {A}_n \models \exists \vec {x}\, \forall \vec {y}\, \neg \Psi (\vec {x}, \vec {y}, [\varphi _0], \dots , [\varphi _{m-1}])$
. The formula
$\prod _C \mathcal {A}_n \models \exists \vec {x}\, \forall \vec {y}\, \neg \Psi (\vec {x}, \vec {y}, [\varphi _0], \dots , [\varphi _{m-1}])$
. The formula
![]() $\neg \Psi $
is uniformly decidable in
$\neg \Psi $
is uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
because
$(\mathcal {A}_n : n \in \mathbb {N})$
because
![]() $\Psi $
is, so applying item (1) to
$\Psi $
is, so applying item (1) to
![]() $\neg \Psi $
yields that
$\neg \Psi $
yields that
Therefore
because the two sets are disjoint.
Lemma 2.6. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
$(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
![]() $\mathfrak {L}$
-structures, and let C be cohesive. Let
$\mathfrak {L}$
-structures, and let C be cohesive. Let
![]() $\Phi (v_0, \dots , v_{m-1})$
be a formula that is logically equivalent to a formula of the form
$\Phi (v_0, \dots , v_{m-1})$
be a formula that is logically equivalent to a formula of the form
![]() $\exists \vec {x}\, \forall \vec {y}\, \Psi _0(\vec {x}, \vec {y}, v_0, \dots , v_{m-1})$
and to a formula of the form
$\exists \vec {x}\, \forall \vec {y}\, \Psi _0(\vec {x}, \vec {y}, v_0, \dots , v_{m-1})$
and to a formula of the form
![]() $\forall \vec {x}\, \exists \vec {y}\, \Psi _1(\vec {x}, \vec {y}, v_0, \dots , v_{m-1})$
, where
$\forall \vec {x}\, \exists \vec {y}\, \Psi _1(\vec {x}, \vec {y}, v_0, \dots , v_{m-1})$
, where
![]() $\Psi _0$
and
$\Psi _0$
and
![]() $\Psi _1$
are uniformly decidable in
$\Psi _1$
are uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
. Then for any
$(\mathcal {A}_n : n \in \mathbb {N})$
. Then for any
![]() $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
,
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
,
Proof The “
![]() $\Rightarrow $
” implication is by Lemma 2.5 item (1) and the equivalence of
$\Rightarrow $
” implication is by Lemma 2.5 item (1) and the equivalence of
![]() $\Phi (\vec {v})$
with
$\Phi (\vec {v})$
with
![]() $\exists \vec {x}\, \forall \vec {y}\, \Psi _0(\vec {x}, \vec {y}, \vec {v})$
. The “
$\exists \vec {x}\, \forall \vec {y}\, \Psi _0(\vec {x}, \vec {y}, \vec {v})$
. The “
![]() $\Leftarrow $
” implication is by Lemma 2.5 item (2) and the equivalence of
$\Leftarrow $
” implication is by Lemma 2.5 item (2) and the equivalence of
![]() $\Phi (\vec {v})$
with
$\Phi (\vec {v})$
with
![]() $\forall \vec {x}\, \exists \vec {y}\, \Psi _1(\vec {x}, \vec {y}, \vec {v})$
.
$\forall \vec {x}\, \exists \vec {y}\, \Psi _1(\vec {x}, \vec {y}, \vec {v})$
.
The following theorem refines the fundamental theorem of cohesive products from [Reference Dimitrov and Harizanov7].
Theorem 2.7. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $(\mathcal {A}_i : i \in \mathbb {N})$
be a sequence of uniformly n-decidable
$(\mathcal {A}_i : i \in \mathbb {N})$
be a sequence of uniformly n-decidable
![]() $\mathfrak {L}$
-structures, and let C be cohesive.
$\mathfrak {L}$
-structures, and let C be cohesive.
-
(1) Let
 $\Phi (v_0, \dots , v_{m-1})$
be a
$\Phi (v_0, \dots , v_{m-1})$
be a
 $\Sigma _{n+2}$
formula. Then for any
$\Sigma _{n+2}$
formula. Then for any
 $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_i|$
,
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_i|$
,  $$ \begin{align*} \prod\nolimits_C \mathcal{A}_i \models \Phi([\varphi_0], \dots, [\varphi_{m-1}]) \quad\Rightarrow\quad C \subseteq^* \bigl\{i : \mathcal{A}_i \models \Phi(\varphi_0(i), \dots, \varphi_{m-1}(i))\bigr\}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathcal{A}_i \models \Phi([\varphi_0], \dots, [\varphi_{m-1}]) \quad\Rightarrow\quad C \subseteq^* \bigl\{i : \mathcal{A}_i \models \Phi(\varphi_0(i), \dots, \varphi_{m-1}(i))\bigr\}. \end{align*} $$
-
(2) Let
 $\Phi (v_0, \dots , v_{m-1})$
be a
$\Phi (v_0, \dots , v_{m-1})$
be a
 $\Pi _{n+2}$
formula. Then for any
$\Pi _{n+2}$
formula. Then for any
 $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_i|$
,
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_i|$
,  $$ \begin{align*} C \subseteq^* \bigl\{i : \mathcal{A}_i \models \Phi(\varphi_0(i), \dots, \varphi_{m-1}(i))\bigr\} \quad\Rightarrow\quad \prod\nolimits_C \mathcal{A}_i \models \Phi([\varphi_0], \dots, [\varphi_{m-1}]). \end{align*} $$
$$ \begin{align*} C \subseteq^* \bigl\{i : \mathcal{A}_i \models \Phi(\varphi_0(i), \dots, \varphi_{m-1}(i))\bigr\} \quad\Rightarrow\quad \prod\nolimits_C \mathcal{A}_i \models \Phi([\varphi_0], \dots, [\varphi_{m-1}]). \end{align*} $$
-
(3) Let
 $\Phi (v_0, \dots , v_{m-1})$
be a
$\Phi (v_0, \dots , v_{m-1})$
be a
 $\Delta _{n+2}$
formula. Then for any
$\Delta _{n+2}$
formula. Then for any
 $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_i|$
,
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_i|$
,  $$ \begin{align*} \prod\nolimits_C \mathcal{A}_i \models \Phi([\varphi_0], \dots, [\varphi_{m-1}]) \quad\Leftrightarrow\quad C \subseteq^* \bigl\{i : \mathcal{A}_i \models \Phi(\varphi_0(i), \dots, \varphi_{m-1}(i))\bigr\}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathcal{A}_i \models \Phi([\varphi_0], \dots, [\varphi_{m-1}]) \quad\Leftrightarrow\quad C \subseteq^* \bigl\{i : \mathcal{A}_i \models \Phi(\varphi_0(i), \dots, \varphi_{m-1}(i))\bigr\}. \end{align*} $$
Proof Item (1) follows from Lemma 2.5 item (1) because a
![]() $\Sigma _{n+2}$
formula
$\Sigma _{n+2}$
formula
![]() $\Phi (v_0, \dots , v_{m-1})$
has the form
$\Phi (v_0, \dots , v_{m-1})$
has the form
![]() $\exists \vec {x}\, \forall \vec {y}\, \Psi (\vec {x}, \vec {y}, v_0, \dots , v_{m-1})$
, where
$\exists \vec {x}\, \forall \vec {y}\, \Psi (\vec {x}, \vec {y}, v_0, \dots , v_{m-1})$
, where
![]() $\Psi (\vec {x}, \vec {y}, v_0, \dots , v_{m-1})$
is
$\Psi (\vec {x}, \vec {y}, v_0, \dots , v_{m-1})$
is
![]() $\Sigma _n$
and hence is uniformly decidable in the uniformly n-decidable sequence
$\Sigma _n$
and hence is uniformly decidable in the uniformly n-decidable sequence
![]() $(\mathcal {A}_i : i \in \mathbb {N})$
. Likewise, item (2) follows from Lemma 2.5 item (2), and item (3) follows from Lemma 2.6.
$(\mathcal {A}_i : i \in \mathbb {N})$
. Likewise, item (2) follows from Lemma 2.5 item (2), and item (3) follows from Lemma 2.6.
Proposition 4.10 shows that Theorem 2.7 is tight in general. We now switch from cohesive products to cohesive powers.
Lemma 2.8. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $\mathcal {A}$
be a computable
$\mathcal {A}$
be a computable
![]() $\mathfrak {L}$
-structure, and let C be cohesive. Let
$\mathfrak {L}$
-structure, and let C be cohesive. Let
![]() $\Phi $
be a sentence of the form
$\Phi $
be a sentence of the form
![]() $\forall \vec {x}\, \exists \vec {y}\, \forall \vec {z} \, \Psi (\vec {x}, \vec {y}, \vec {z})$
, where
$\forall \vec {x}\, \exists \vec {y}\, \forall \vec {z} \, \Psi (\vec {x}, \vec {y}, \vec {z})$
, where
![]() $\Psi (\vec {x}, \vec {y}, \vec {z})$
is decidable in
$\Psi (\vec {x}, \vec {y}, \vec {z})$
is decidable in
![]() $\mathcal {A}$
. Then
$\mathcal {A}$
. Then
Proof Suppose that
![]() $\prod _C \mathcal {A} \models \Phi $
. Write
$\prod _C \mathcal {A} \models \Phi $
. Write
![]() $\vec {x} = x_0, \dots , x_{m-1}$
. For each
$\vec {x} = x_0, \dots , x_{m-1}$
. For each
![]() $i < m$
, fix an
$i < m$
, fix an
![]() $a_i \in |\mathcal {A}|$
, and let
$a_i \in |\mathcal {A}|$
, and let
![]() $\varphi _i$
be the constant function with value
$\varphi _i$
be the constant function with value
![]() $a_i$
. Then
$a_i$
. Then
![]() $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}|$
, so
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}|$
, so
Therefore
by Lemma 2.5 item (1) applied to the formula
![]() $\exists \vec {y}\, \forall \vec {z} \, \Psi (\vec {x}, \vec {y}, \vec {z})$
and the sequence of structures
$\exists \vec {y}\, \forall \vec {z} \, \Psi (\vec {x}, \vec {y}, \vec {z})$
and the sequence of structures
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
where
$(\mathcal {A}_n : n \in \mathbb {N})$
where
![]() $\mathcal {A}_n$
is
$\mathcal {A}_n$
is
![]() $\mathcal {A}$
for each n. It must therefore be that
$\mathcal {A}$
for each n. It must therefore be that
![]() $\mathcal {A} \models \exists \vec {y}\, \forall \vec {z}\, \Psi (a_0, \dots , a_{m-1}, \vec {y}, \vec {z})$
. The sequence
$\mathcal {A} \models \exists \vec {y}\, \forall \vec {z}\, \Psi (a_0, \dots , a_{m-1}, \vec {y}, \vec {z})$
. The sequence
![]() $a_0, \dots , a_{m-1} \in |\mathcal {A}|$
was arbitrary, so we have shown that
$a_0, \dots , a_{m-1} \in |\mathcal {A}|$
was arbitrary, so we have shown that
![]() $\mathcal {A} \models \forall \vec {x}\, \exists \vec {y}\, \forall \vec {z} \, \Psi (\vec {x}, \vec {y}, \vec {z})$
. That is,
$\mathcal {A} \models \forall \vec {x}\, \exists \vec {y}\, \forall \vec {z} \, \Psi (\vec {x}, \vec {y}, \vec {z})$
. That is,
![]() $\mathcal {A} \models \Phi $
.
$\mathcal {A} \models \Phi $
.
The next theorem is our version of Łoś’s theorem for cohesive powers of n-decidable structures, which refines the fundamental theorem of cohesive powers from [Reference Dimitrov4].
Theorem 2.9. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $\mathcal {A}$
be an n-decidable
$\mathcal {A}$
be an n-decidable
![]() $\mathfrak {L}$
-structure, and let C be a cohesive set.
$\mathfrak {L}$
-structure, and let C be a cohesive set.
-
(1) Let
 $\Phi (v_0, \dots , v_{m-1})$
be a
$\Phi (v_0, \dots , v_{m-1})$
be a
 $\Delta _{n+2}$
formula. Then for any
$\Delta _{n+2}$
formula. Then for any
 $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}|$
,
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}|$
,  $$ \begin{align*} \prod\nolimits_C \mathcal{A} \models \Phi([\varphi_0], \dots, [\varphi_{m-1}]) \quad\Leftrightarrow\quad C \subseteq^* \bigl\{n : \mathcal{A} \models \Phi(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathcal{A} \models \Phi([\varphi_0], \dots, [\varphi_{m-1}]) \quad\Leftrightarrow\quad C \subseteq^* \bigl\{n : \mathcal{A} \models \Phi(\varphi_0(n), \dots, \varphi_{m-1}(n))\bigr\}. \end{align*} $$
-
(2) Let
 $\Phi $
be a
$\Phi $
be a
 $\Delta _{n+3}$
sentence. Then
$\Delta _{n+3}$
sentence. Then
 $\mathcal {A} \models \Phi $
if and only if
$\mathcal {A} \models \Phi $
if and only if
 $\prod _C \mathcal {A} \models \Phi $
.
$\prod _C \mathcal {A} \models \Phi $
. -
(3) Let
 $\Phi $
be a
$\Phi $
be a
 $\Sigma _{n+3}$
sentence. If
$\Sigma _{n+3}$
sentence. If
 $\mathcal {A} \models \Phi $
, then
$\mathcal {A} \models \Phi $
, then
 $\prod _C \mathcal {A} \models \Phi $
.
$\prod _C \mathcal {A} \models \Phi $
.
Proof Item (1) is the special case of Theorem 2.7 item (3) in which each structure
![]() $\mathcal {A}_i$
is
$\mathcal {A}_i$
is
![]() $\mathcal {A}$
. Item (2) follows from item (3) because if
$\mathcal {A}$
. Item (2) follows from item (3) because if
![]() $\Phi $
is a
$\Phi $
is a
![]() $\Delta _{n+3}$
sentence, then both
$\Delta _{n+3}$
sentence, then both
![]() $\Phi $
and
$\Phi $
and
![]() $\neg \Phi $
are logically equivalent to
$\neg \Phi $
are logically equivalent to
![]() $\Sigma _{n+3}$
sentences. For item (3), consider the sentence
$\Sigma _{n+3}$
sentences. For item (3), consider the sentence
![]() $\neg \Phi $
, which is logically equivalent to a
$\neg \Phi $
, which is logically equivalent to a
![]() $\Pi _{n+3}$
sentence
$\Pi _{n+3}$
sentence
![]() $\Theta $
. The sentence
$\Theta $
. The sentence
![]() $\Theta $
thus has the form
$\Theta $
thus has the form
![]() $\forall \vec {x}\, \exists \vec {y}\, \forall \vec {z} \, \Psi (\vec {x}, \vec {y}, \vec {z})$
, where
$\forall \vec {x}\, \exists \vec {y}\, \forall \vec {z} \, \Psi (\vec {x}, \vec {y}, \vec {z})$
, where
![]() $\Psi (\vec {x}, \vec {y}, \vec {z})$
is
$\Psi (\vec {x}, \vec {y}, \vec {z})$
is
![]() $\Sigma _n$
. The formula
$\Sigma _n$
. The formula
![]() $\Psi (\vec {x}, \vec {y}, \vec {z})$
is decidable in
$\Psi (\vec {x}, \vec {y}, \vec {z})$
is decidable in
![]() $\mathcal {A}$
because
$\mathcal {A}$
because
![]() $\mathcal {A}$
is n-decidable. Therefore
$\mathcal {A}$
is n-decidable. Therefore
![]() $\prod _C \mathcal {A} \models \Theta $
implies that
$\prod _C \mathcal {A} \models \Theta $
implies that
![]() $\mathcal {A} \models \Theta $
by Lemma 2.8. The contrapositive yields that
$\mathcal {A} \models \Theta $
by Lemma 2.8. The contrapositive yields that
![]() $\mathcal {A} \models \Phi $
implies that
$\mathcal {A} \models \Phi $
implies that
![]() $\prod _C \mathcal {A} \models \Phi $
.
$\prod _C \mathcal {A} \models \Phi $
.
Corollary 4.9 shows that Theorem 2.9 item (3) is tight in general. As mentioned above, we recover Łoś’s theorem for all first-order sentences when we consider cohesive powers of decidable structures. This is essentially the same as Nelson’s [Reference Nelson20, Theorem 0.5]. See also [Reference Dimitrov4].
Corollary 2.10. Let
![]() $\mathfrak {L}$
be a computable language, and let C be a cohesive set.
$\mathfrak {L}$
be a computable language, and let C be a cohesive set.
-
(1) Let
 $(\mathcal {A}_i : i \in \mathbb {N})$
be a sequence of uniformly decidable
$(\mathcal {A}_i : i \in \mathbb {N})$
be a sequence of uniformly decidable
 $\mathfrak {L}$
-structures, and let
$\mathfrak {L}$
-structures, and let
 $\Phi (v_0, \dots , v_{m-1})$
be a formula with all free variables displayed. Then for any
$\Phi (v_0, \dots , v_{m-1})$
be a formula with all free variables displayed. Then for any
 $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_i|$
,
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_i|$
,  $$ \begin{align*} \prod\nolimits_C \mathcal{A}_i \models \Phi([\varphi_0], \dots, [\varphi_{m-1}]) \quad\Leftrightarrow\quad C \subseteq^* \bigl\{i : \mathcal{A}_i \models \Phi(\varphi_0(i), \dots, \varphi_{m-1}(i))\bigr\}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathcal{A}_i \models \Phi([\varphi_0], \dots, [\varphi_{m-1}]) \quad\Leftrightarrow\quad C \subseteq^* \bigl\{i : \mathcal{A}_i \models \Phi(\varphi_0(i), \dots, \varphi_{m-1}(i))\bigr\}. \end{align*} $$
In particular, if
 $\Phi $
is a sentence, then
$\Phi $
is a sentence, then  $$ \begin{align*} \prod\nolimits_C \mathcal{A}_i \models \Phi \quad\Leftrightarrow\quad C \subseteq^* \{i : \mathcal{A}_i \models \Phi\}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathcal{A}_i \models \Phi \quad\Leftrightarrow\quad C \subseteq^* \{i : \mathcal{A}_i \models \Phi\}. \end{align*} $$
-
(2) If
 $\mathcal {A}$
is a decidable
$\mathcal {A}$
is a decidable
 $\mathfrak {L}$
-structure, then
$\mathfrak {L}$
-structure, then
 $\mathcal {A}$
and
$\mathcal {A}$
and
 $\prod _C \mathcal {A}$
are elementarily equivalent.
$\prod _C \mathcal {A}$
are elementarily equivalent.
Proof Item (1) follows from Theorem 2.7 because the structures
![]() $(\mathcal {A}_i : i \in \mathbb {N})$
are uniformly n-decidable for every n. Item (2) follows from the special case of item (1) in which
$(\mathcal {A}_i : i \in \mathbb {N})$
are uniformly n-decidable for every n. Item (2) follows from the special case of item (1) in which
![]() $\mathcal {A}_i$
is
$\mathcal {A}_i$
is
![]() $\mathcal {A}$
for each i. Item (2) also follows from Theorem 2.9 item (2) because
$\mathcal {A}$
for each i. Item (2) also follows from Theorem 2.9 item (2) because
![]() $\mathcal {A}$
is n-decidable for every n.
$\mathcal {A}$
is n-decidable for every n.
We pause to point out that we can recover a version of Skolem’s countable non-standard model of arithmetic by relativizing everything to
![]() $0^{(\omega )}$
, the
$0^{(\omega )}$
, the
![]() $\omega $
th Turing jump of
$\omega $
th Turing jump of
![]() $0$
. Let
$0$
. Let
![]() $\mathcal {N} = (\mathbb {N}, +, \times , <)$
denote the standard model of arithmetic. Then
$\mathcal {N} = (\mathbb {N}, +, \times , <)$
denote the standard model of arithmetic. Then
![]() $\mathcal {N}$
is a decidable structure relative to
$\mathcal {N}$
is a decidable structure relative to
![]() $0^{(\omega )}$
. Therefore
$0^{(\omega )}$
. Therefore
![]() $\mathcal {N} \equiv \prod _C^{0^{(\omega )}} \mathcal {N}$
for any C that is cohesive relative to
$\mathcal {N} \equiv \prod _C^{0^{(\omega )}} \mathcal {N}$
for any C that is cohesive relative to
![]() $0^{(\omega )}$
by the relativized version of Corollary 2.10. Thus
$0^{(\omega )}$
by the relativized version of Corollary 2.10. Thus
![]() $\prod _C^{0^{(\omega )}} \mathcal {N}$
is a countable non-standard model of arithmetic. The superscript
$\prod _C^{0^{(\omega )}} \mathcal {N}$
is a countable non-standard model of arithmetic. The superscript
![]() $0^{(\omega )}$
in
$0^{(\omega )}$
in
![]() $\prod _C^{0^{(\omega )}} \mathcal {N}$
indicates that we relativize the cohesive power construction to
$\prod _C^{0^{(\omega )}} \mathcal {N}$
indicates that we relativize the cohesive power construction to
![]() $0^{(\omega )}$
by requiring that C be cohesive for the collection of sets that are c.e. relative to
$0^{(\omega )}$
by requiring that C be cohesive for the collection of sets that are c.e. relative to
![]() $0^{(\omega )}$
and by building the cohesive power from functions that are partial computable relative to
$0^{(\omega )}$
and by building the cohesive power from functions that are partial computable relative to
![]() $0^{(\omega )}$
.
$0^{(\omega )}$
.
2.3 Reducts, substructures, and disjoint unions
Cohesive products respect reducts of computable structures. Let
![]() $\mathfrak {L} \subseteq \mathfrak {L}^+$
be two languages, and let
$\mathfrak {L} \subseteq \mathfrak {L}^+$
be two languages, and let
![]() $\mathcal {A}$
be an
$\mathcal {A}$
be an
![]() $\mathfrak {L}^+$
-structure. Then the reduct
$\mathfrak {L}^+$
-structure. Then the reduct
![]() $\mathcal {A} {\restriction } \mathfrak {L}$
of
$\mathcal {A} {\restriction } \mathfrak {L}$
of
![]() $\mathcal {A}$
to
$\mathcal {A}$
to
![]() $\mathfrak {L}$
is the
$\mathfrak {L}$
is the
![]() $\mathfrak {L}$
-structure obtained from
$\mathfrak {L}$
-structure obtained from
![]() $\mathcal {A}$
by forgetting about the symbols of
$\mathcal {A}$
by forgetting about the symbols of
![]() $\mathfrak {L}^+ \setminus \mathfrak {L}$
. If
$\mathfrak {L}^+ \setminus \mathfrak {L}$
. If
![]() $\mathfrak {L} \subseteq \mathfrak {L}^+$
are computable languages and
$\mathfrak {L} \subseteq \mathfrak {L}^+$
are computable languages and
![]() $\mathcal {A}$
is a computable
$\mathcal {A}$
is a computable
![]() $\mathfrak {L}^+$
-structure, then
$\mathfrak {L}^+$
-structure, then
![]() $\mathcal {A} {\restriction } \mathfrak {L}$
is a computable
$\mathcal {A} {\restriction } \mathfrak {L}$
is a computable
![]() $\mathfrak {L}$
-structure.
$\mathfrak {L}$
-structure.
Many of our arguments make implicit use of the following proposition.
Proposition 2.11. Let
![]() $\mathfrak {L} \subseteq \mathfrak {L}^+$
be computable languages, let
$\mathfrak {L} \subseteq \mathfrak {L}^+$
be computable languages, let
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
$(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
![]() $\mathfrak {L}^+$
-structures, and let C be a cohesive set. Then
$\mathfrak {L}^+$
-structures, and let C be a cohesive set. Then
Thus in the case of a single computable
![]() $\mathfrak {L}^+$
-structure
$\mathfrak {L}^+$
-structure
![]() $\mathcal {A}$
,
$\mathcal {A}$
,
Proof The
![]() $\mathfrak {L}$
-structures
$\mathfrak {L}$
-structures
![]() $\prod _C (\mathcal {A}_n {\restriction } \mathfrak {L})$
and
$\prod _C (\mathcal {A}_n {\restriction } \mathfrak {L})$
and
![]() $\bigl ( \prod _C \mathcal {A}_n \bigr ) {\restriction } \mathfrak {L}$
share the same domain, which is the set of all
$\bigl ( \prod _C \mathcal {A}_n \bigr ) {\restriction } \mathfrak {L}$
share the same domain, which is the set of all
![]() $=_C$
-equivalence classes
$=_C$
-equivalence classes
![]() $[\varphi ]$
of partial computable functions
$[\varphi ]$
of partial computable functions
![]() $\varphi $
such that
$\varphi $
such that
![]() $\forall n \, (\varphi (n){\downarrow } \,\rightarrow \, \varphi (n) \in |\mathcal {A}_n|)$
and
$\forall n \, (\varphi (n){\downarrow } \,\rightarrow \, \varphi (n) \in |\mathcal {A}_n|)$
and
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
. One then checks that the identity map is the desired isomorphism.
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
. One then checks that the identity map is the desired isomorphism.
Cohesive powers respect computable substructures and finite disjoint unions of computable structures.
Proposition 2.12. Let
![]() $\mathfrak {L}$
be a computable language with a unary relation symbol U. Let
$\mathfrak {L}$
be a computable language with a unary relation symbol U. Let
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
$(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
![]() $\mathfrak {L}$
-structures, and suppose that
$\mathfrak {L}$
-structures, and suppose that
![]() $\{a \in |\mathcal {A}_n| : \mathcal {A}_n \models U(a)\}$
forms the domain of a computable substructure
$\{a \in |\mathcal {A}_n| : \mathcal {A}_n \models U(a)\}$
forms the domain of a computable substructure
![]() $\mathcal {B}_n$
of
$\mathcal {B}_n$
of
![]() $\mathcal {A}_n$
for every n. Let C be a cohesive set. Then
$\mathcal {A}_n$
for every n. Let C be a cohesive set. Then
![]() $\bigl \{[\varphi ] \in |\prod _C \mathcal {A}_n| : \prod _C \mathcal {A}_n \models U([\varphi ])\bigr \}$
forms the domain of a substructure
$\bigl \{[\varphi ] \in |\prod _C \mathcal {A}_n| : \prod _C \mathcal {A}_n \models U([\varphi ])\bigr \}$
forms the domain of a substructure
![]() $\mathcal {D}$
of
$\mathcal {D}$
of
![]() $\prod _C \mathcal {A}_n$
, and
$\prod _C \mathcal {A}_n$
, and
![]() $\prod _C \mathcal {B}_n \cong \mathcal {D}$
.
$\prod _C \mathcal {B}_n \cong \mathcal {D}$
.
Proof Let f be an m-ary function symbol of
![]() $\mathfrak {L}$
, and let
$\mathfrak {L}$
, and let
![]() $[\varphi _0], \dots , [\varphi _{m-1}]$
be elements of
$[\varphi _0], \dots , [\varphi _{m-1}]$
be elements of
![]() $\{[\varphi ] \in |\prod _C \mathcal {A}_n| : \prod _C \mathcal {A}_n \models U([\varphi ])\}$
. Then
$\{[\varphi ] \in |\prod _C \mathcal {A}_n| : \prod _C \mathcal {A}_n \models U([\varphi ])\}$
. Then
![]() $(\forall ^\infty n \in C)(\mathcal {A}_n \models \bigwedge _{i < m} U(\varphi _i(n)))$
, so
$(\forall ^\infty n \in C)(\mathcal {A}_n \models \bigwedge _{i < m} U(\varphi _i(n)))$
, so
![]() $(\forall ^\infty n \in C)\bigl [\mathcal {A}_n \models U(f(\varphi _0(n), \dots , \varphi _{m-1}(n)))\bigr ]$
because
$(\forall ^\infty n \in C)\bigl [\mathcal {A}_n \models U(f(\varphi _0(n), \dots , \varphi _{m-1}(n)))\bigr ]$
because
![]() $\{a \in |\mathcal {A}_n| : \mathcal {A}_n \models U(a)\}$
is closed under
$\{a \in |\mathcal {A}_n| : \mathcal {A}_n \models U(a)\}$
is closed under
![]() $f^{\mathcal {A}_n}$
as it is the domain of the substructure
$f^{\mathcal {A}_n}$
as it is the domain of the substructure
![]() $\mathcal {B}_n$
. Therefore
$\mathcal {B}_n$
. Therefore
![]() $\prod _C \mathcal {A}_n \models U(f([\varphi _0], \dots , [\varphi _{m-1}]))$
by Theorem 2.7 item (3). Thus
$\prod _C \mathcal {A}_n \models U(f([\varphi _0], \dots , [\varphi _{m-1}]))$
by Theorem 2.7 item (3). Thus
![]() $\bigl \{[\varphi ] \in |\prod _C \mathcal {A}_n| : \prod _C \mathcal {A}_n \models U([\varphi ])\bigr \}$
is closed under
$\bigl \{[\varphi ] \in |\prod _C \mathcal {A}_n| : \prod _C \mathcal {A}_n \models U([\varphi ])\bigr \}$
is closed under
![]() $f^{\prod _C \mathcal {A}_n}$
. Similar reasoning shows that
$f^{\prod _C \mathcal {A}_n}$
. Similar reasoning shows that
![]() $\prod _C \mathcal {A}_n \models U(c)$
for every constant symbol c of
$\prod _C \mathcal {A}_n \models U(c)$
for every constant symbol c of
![]() $\mathfrak {L}$
. Thus
$\mathfrak {L}$
. Thus
![]() $\bigl \{[\varphi ] \in |\prod _C \mathcal {A}_n| : \prod _C \mathcal {A}_n \models U([\varphi ])\bigr \}$
forms the domain of a substructure of
$\bigl \{[\varphi ] \in |\prod _C \mathcal {A}_n| : \prod _C \mathcal {A}_n \models U([\varphi ])\bigr \}$
forms the domain of a substructure of
![]() $\prod _C \mathcal {A}_n$
.
$\prod _C \mathcal {A}_n$
.
Recall that
![]() $\mathcal {B}_n$
is the substructure of
$\mathcal {B}_n$
is the substructure of
![]() $\mathcal {A}_n$
with domain
$\mathcal {A}_n$
with domain
![]() $\{a \in |\mathcal {A}_n| : \mathcal {A}_n \models U(a)\}$
for each n, and let
$\{a \in |\mathcal {A}_n| : \mathcal {A}_n \models U(a)\}$
for each n, and let
![]() $\mathcal {D}$
be the substructure of
$\mathcal {D}$
be the substructure of
![]() $\prod _C \mathcal {A}_n$
with domain
$\prod _C \mathcal {A}_n$
with domain
![]() $\bigl \{[\varphi ] \in |\prod _C \mathcal {A}_n| : \prod _C \mathcal {A}_n \models U([\varphi ])\bigr \}$
. In view of the comment following Definition 2.2, the domains of
$\bigl \{[\varphi ] \in |\prod _C \mathcal {A}_n| : \prod _C \mathcal {A}_n \models U([\varphi ])\bigr \}$
. In view of the comment following Definition 2.2, the domains of
![]() $\prod _C \mathcal {B}_n$
and of
$\prod _C \mathcal {B}_n$
and of
![]() $\mathcal {D}$
are in both cases the
$\mathcal {D}$
are in both cases the
![]() $=_C$
-equivalence classes of partial computable functions
$=_C$
-equivalence classes of partial computable functions
![]() $\varphi $
such that
$\varphi $
such that
![]() $(\forall ^\infty n \in C)\bigl (\varphi (n){\downarrow } \,\wedge \, U^{\mathcal {A}_n}(\varphi (n))\bigr )$
. One may then check that the map
$(\forall ^\infty n \in C)\bigl (\varphi (n){\downarrow } \,\wedge \, U^{\mathcal {A}_n}(\varphi (n))\bigr )$
. One may then check that the map
![]() $[\varphi ] \mapsto [\varphi ]$
from
$[\varphi ] \mapsto [\varphi ]$
from
![]() $\prod _C \mathcal {B}_n$
to
$\prod _C \mathcal {B}_n$
to
![]() $\mathcal {D}$
is an isomorphism.
$\mathcal {D}$
is an isomorphism.
We usually apply Proposition 2.12 in the case of a single computable structure
![]() $\mathcal {A}$
. In this situation, the proposition says that if
$\mathcal {A}$
. In this situation, the proposition says that if
![]() $\mathcal {A}$
is a computable structure, if
$\mathcal {A}$
is a computable structure, if
![]() $\{a \in |\mathcal {A}| : \mathcal {A} \models U(a)\}$
forms the domain of a computable substructure
$\{a \in |\mathcal {A}| : \mathcal {A} \models U(a)\}$
forms the domain of a computable substructure
![]() $\mathcal {B}$
of
$\mathcal {B}$
of
![]() $\mathcal {A}$
, and if C is cohesive, then
$\mathcal {A}$
, and if C is cohesive, then
![]() $\bigl \{[\varphi ] \in |\prod _C \mathcal {A}| : \prod _C \mathcal {A} \models U([\varphi ])\bigr \}$
forms the domain of a substructure
$\bigl \{[\varphi ] \in |\prod _C \mathcal {A}| : \prod _C \mathcal {A} \models U([\varphi ])\bigr \}$
forms the domain of a substructure
![]() $\mathcal {D}$
of
$\mathcal {D}$
of
![]() $\prod _C \mathcal {A}$
with
$\prod _C \mathcal {A}$
with
![]() $\prod _C \mathcal {B} \cong \mathcal {D}$
.
$\prod _C \mathcal {B} \cong \mathcal {D}$
.
Definition 2.13. Let
![]() $\mathfrak {L}$
be a relational language, and let
$\mathfrak {L}$
be a relational language, and let
![]() $\mathcal {A}_0, \dots , \mathcal {A}_{k-1}$
be
$\mathcal {A}_0, \dots , \mathcal {A}_{k-1}$
be
![]() $\mathfrak {L}$
-structures for some
$\mathfrak {L}$
-structures for some
![]() $k> 0$
. The disjoint union of
$k> 0$
. The disjoint union of
![]() $\mathcal {A}_0, \dots , \mathcal {A}_{k-1}$
is the
$\mathcal {A}_0, \dots , \mathcal {A}_{k-1}$
is the
![]() $\mathfrak {L}$
-structure
$\mathfrak {L}$
-structure
![]() $\bigsqcup _{i < k} \mathcal {A}_i$
with domain
$\bigsqcup _{i < k} \mathcal {A}_i$
with domain
![]() $\bigcup _{i < k}(\{i\} \times |\mathcal {A}_i|)$
defined as follows. For every m-ary relation symbol R and every
$\bigcup _{i < k}(\{i\} \times |\mathcal {A}_i|)$
defined as follows. For every m-ary relation symbol R and every
![]() $(i_0, x_0), \dots , (i_{m-1}, x_{m-1}) \in \bigl |\bigsqcup _{i < k} \mathcal {A}_i\bigr |$
, the relation
$(i_0, x_0), \dots , (i_{m-1}, x_{m-1}) \in \bigl |\bigsqcup _{i < k} \mathcal {A}_i\bigr |$
, the relation
![]() $R^{\bigsqcup _{i < k} \mathcal {A}_i}((i_0, x_0), \dots , (i_{m-1}, x_{m-1}))$
holds if and only if
$R^{\bigsqcup _{i < k} \mathcal {A}_i}((i_0, x_0), \dots , (i_{m-1}, x_{m-1}))$
holds if and only if
![]() $i_0 = \cdots = i_{m-1} = i$
for some
$i_0 = \cdots = i_{m-1} = i$
for some
![]() $i < k$
and
$i < k$
and
![]() $R^{\mathcal {A}_i}(x_0, \dots , x_{m-1})$
holds.
$R^{\mathcal {A}_i}(x_0, \dots , x_{m-1})$
holds.
In the case of computable
![]() $\mathfrak {L}$
-structures
$\mathfrak {L}$
-structures
![]() $\mathcal {A}_0, \dots , \mathcal {A}_{k-1}$
for a computable relational language
$\mathcal {A}_0, \dots , \mathcal {A}_{k-1}$
for a computable relational language
![]() $\mathfrak {L}$
, one may use the pairing function to compute a copy of
$\mathfrak {L}$
, one may use the pairing function to compute a copy of
![]() $\bigsqcup _{i < k} \mathcal {A}_i$
. Thus if
$\bigsqcup _{i < k} \mathcal {A}_i$
. Thus if
![]() $\mathcal {A}_0, \dots , \mathcal {A}_{k-1}$
are computable structures, then so is
$\mathcal {A}_0, \dots , \mathcal {A}_{k-1}$
are computable structures, then so is
![]() $\bigsqcup _{i < k} \mathcal {A}_i$
.
$\bigsqcup _{i < k} \mathcal {A}_i$
.
Proposition 2.14. Let
![]() $\mathfrak {L}$
be a computable relational language, let
$\mathfrak {L}$
be a computable relational language, let
![]() $\mathcal {A}_0, \dots , \mathcal {A}_{k-1}$
be computable
$\mathcal {A}_0, \dots , \mathcal {A}_{k-1}$
be computable
![]() $\mathfrak {L}$
-structures for some
$\mathfrak {L}$
-structures for some
![]() $k> 0$
, and let C be cohesive. Then
$k> 0$
, and let C be cohesive. Then
 $$ \begin{align*} \prod\nolimits_C\left(\bigsqcup_{i < k} \mathcal{A}_i\right) \;\cong\; \bigsqcup_{i < k}\left(\prod\nolimits_C \mathcal{A}_i\right). \end{align*} $$
$$ \begin{align*} \prod\nolimits_C\left(\bigsqcup_{i < k} \mathcal{A}_i\right) \;\cong\; \bigsqcup_{i < k}\left(\prod\nolimits_C \mathcal{A}_i\right). \end{align*} $$
Proof Expand
![]() $\mathfrak {L}$
to
$\mathfrak {L}$
to
![]() $\mathfrak {L}^+ = \mathfrak {L} \cup \{U_0, \dots , U_{k-1}\}$
, where
$\mathfrak {L}^+ = \mathfrak {L} \cup \{U_0, \dots , U_{k-1}\}$
, where
![]() $U_0, \dots , U_{k-1}$
are k fresh unary relation symbols. Expand
$U_0, \dots , U_{k-1}$
are k fresh unary relation symbols. Expand
![]() $\bigsqcup _{i < k} \mathcal {A}_i$
to a computable
$\bigsqcup _{i < k} \mathcal {A}_i$
to a computable
![]() $\mathfrak {L}^+$
-structure by interpreting
$\mathfrak {L}^+$
-structure by interpreting
![]() $U_i$
as the domain of
$U_i$
as the domain of
![]() $\mathcal {A}_i$
for each
$\mathcal {A}_i$
for each
![]() $i < k$
:
$i < k$
:
![]() $U_i^{\bigsqcup _{i < k} \mathcal {A}_i}(x)$
holds if and only if
$U_i^{\bigsqcup _{i < k} \mathcal {A}_i}(x)$
holds if and only if
![]() $\pi _0(x) = i$
. Then for each
$\pi _0(x) = i$
. Then for each
![]() $x \in \bigl |\bigsqcup _{i < k} \mathcal {A}_i\bigr |$
there is a unique
$x \in \bigl |\bigsqcup _{i < k} \mathcal {A}_i\bigr |$
there is a unique
![]() $i < k$
for which
$i < k$
for which
![]() $U_i^{\bigsqcup _{i < k} \mathcal {A}_i}(x)$
holds:
$U_i^{\bigsqcup _{i < k} \mathcal {A}_i}(x)$
holds:
 $$ \begin{align} \bigsqcup_{i < k} \mathcal{A}_i \models \forall x\, \left[ \left( \bigvee_{i < k}U_i(x) \right) \;\wedge\; \left( \bigwedge_{\substack{i,j < k \\ i \neq j}}(U_i(x) \rightarrow \neg U_j(x)) \right) \right]. \end{align} $$
$$ \begin{align} \bigsqcup_{i < k} \mathcal{A}_i \models \forall x\, \left[ \left( \bigvee_{i < k}U_i(x) \right) \;\wedge\; \left( \bigwedge_{\substack{i,j < k \\ i \neq j}}(U_i(x) \rightarrow \neg U_j(x)) \right) \right]. \end{align} $$
Furthermore, for each m-ary relation symbol
![]() $R \in \mathfrak {L}$
, if
$R \in \mathfrak {L}$
, if
![]() $R^{\bigsqcup _{i < k} \mathcal {A}_i}(x_0, \dots , x_{m-1})$
holds for some
$R^{\bigsqcup _{i < k} \mathcal {A}_i}(x_0, \dots , x_{m-1})$
holds for some
![]() $x_0, \dots , x_{m-1} \in \bigl |\bigsqcup _{i < k} \mathcal {A}_i\bigr |$
, then there is an
$x_0, \dots , x_{m-1} \in \bigl |\bigsqcup _{i < k} \mathcal {A}_i\bigr |$
, then there is an
![]() $i < k$
such that
$i < k$
such that
![]() $U_i^{\bigsqcup _{i < k} \mathcal {A}_i}(x_j)$
holds for all
$U_i^{\bigsqcup _{i < k} \mathcal {A}_i}(x_j)$
holds for all
![]() $j < m$
:
$j < m$
:
 $$ \begin{align} \bigsqcup_{i < k} \mathcal{A}_i \models \forall x_0, \dots, x_{m-1}\, \left[ R(x_0, \dots, x_{m-1}) \;\rightarrow\; \bigvee_{i < k}\bigwedge_{j < m} U_i(x_j) \right]. \end{align} $$
$$ \begin{align} \bigsqcup_{i < k} \mathcal{A}_i \models \forall x_0, \dots, x_{m-1}\, \left[ R(x_0, \dots, x_{m-1}) \;\rightarrow\; \bigvee_{i < k}\bigwedge_{j < m} U_i(x_j) \right]. \end{align} $$
The
![]() $\mathfrak {L}^+$
-sentences in (*) and (⋆) are
$\mathfrak {L}^+$
-sentences in (*) and (⋆) are
![]() $\Pi _1$
; therefore
$\Pi _1$
; therefore
![]() $\prod _C (\bigsqcup _{i < k} \mathcal {A}_i)$
also satisfies all of these sentences by Theorem 2.9 item (2). For each
$\prod _C (\bigsqcup _{i < k} \mathcal {A}_i)$
also satisfies all of these sentences by Theorem 2.9 item (2). For each
![]() $i < k$
, let
$i < k$
, let
![]() $\mathcal {D}_i$
be the
$\mathcal {D}_i$
be the
![]() $\mathfrak {L}$
-substructure of
$\mathfrak {L}$
-substructure of
![]() $\prod _C (\bigsqcup _{i < k} \mathcal {A}_i)$
whose domain consists of the
$\prod _C (\bigsqcup _{i < k} \mathcal {A}_i)$
whose domain consists of the
![]() $[\varphi ]$
for which
$[\varphi ]$
for which
![]() $\prod _C (\bigsqcup _{i < k} \mathcal {A}_i) \models U_i([\varphi ])$
. Then
$\prod _C (\bigsqcup _{i < k} \mathcal {A}_i) \models U_i([\varphi ])$
. Then
![]() $\prod _C (\bigsqcup _{i < k} \mathcal {A}_i) \cong \bigsqcup _{i < k} \mathcal {D}_i$
as
$\prod _C (\bigsqcup _{i < k} \mathcal {A}_i) \cong \bigsqcup _{i < k} \mathcal {D}_i$
as
![]() $\mathfrak {L}$
-structures. This is because each
$\mathfrak {L}$
-structures. This is because each
![]() $[\varphi ] \in \bigl |\prod _C (\bigsqcup _{i < k} \mathcal {A}_i)\bigr |$
is in
$[\varphi ] \in \bigl |\prod _C (\bigsqcup _{i < k} \mathcal {A}_i)\bigr |$
is in
![]() $|\mathcal {D}_i|$
for exactly one
$|\mathcal {D}_i|$
for exactly one
![]() $i < k$
; and if
$i < k$
; and if
![]() $R^{\prod _C (\bigsqcup _{i < k} \mathcal {A}_i)}([\varphi _0], \dots , [\varphi _{m-1}])$
holds for an m-ary relation symbol
$R^{\prod _C (\bigsqcup _{i < k} \mathcal {A}_i)}([\varphi _0], \dots , [\varphi _{m-1}])$
holds for an m-ary relation symbol
![]() $R \in \mathfrak {L}$
and
$R \in \mathfrak {L}$
and
![]() $[\varphi _0], \dots , [\varphi _{m-1}] \in \bigl |\prod _C (\bigsqcup _{i < k} \mathcal {A}_i)\bigr |$
, then
$[\varphi _0], \dots , [\varphi _{m-1}] \in \bigl |\prod _C (\bigsqcup _{i < k} \mathcal {A}_i)\bigr |$
, then
![]() $[\varphi _0], \dots , [\varphi _{m-1}]$
must all be in
$[\varphi _0], \dots , [\varphi _{m-1}]$
must all be in
![]() $|\mathcal {D}_i|$
for the same
$|\mathcal {D}_i|$
for the same
![]() $i < k$
. We have that
$i < k$
. We have that
![]() $\mathcal {D}_i \cong \prod _C \mathcal {A}_i$
as
$\mathcal {D}_i \cong \prod _C \mathcal {A}_i$
as
![]() $\mathfrak {L}$
-structures for each
$\mathfrak {L}$
-structures for each
![]() $i < k$
by Proposition 2.12, so
$i < k$
by Proposition 2.12, so
![]() $\prod _C\Bigl (\bigsqcup _{i < k} \mathcal {A}_i\Bigr ) \;\cong \; \bigsqcup _{i < k}(\prod _C \mathcal {A}_i)$
as
$\prod _C\Bigl (\bigsqcup _{i < k} \mathcal {A}_i\Bigr ) \;\cong \; \bigsqcup _{i < k}(\prod _C \mathcal {A}_i)$
as
![]() $\mathfrak {L}$
-structures.
$\mathfrak {L}$
-structures.
2.4 Saturation
There are many classical results concerning the saturation of ultraproducts. See, for example, [Reference Chang and Keisler2, Section 6.1]. One well-known result is that, for a countable language, ultraproducts over countably incomplete ultrafilters are always
![]() $\aleph _1$
-saturated (see [Reference Chang and Keisler2, Theorem 6.1.1]). Here we show that cohesive products of uniformly decidable structures are always recursively saturated (which is essentially due to Nelson [Reference Nelson20]) and that, for
$\aleph _1$
-saturated (see [Reference Chang and Keisler2, Theorem 6.1.1]). Here we show that cohesive products of uniformly decidable structures are always recursively saturated (which is essentially due to Nelson [Reference Nelson20]) and that, for
![]() $n> 0$
, cohesive products of uniformly n-decidable structures are always
$n> 0$
, cohesive products of uniformly n-decidable structures are always
![]() $\Sigma _n$
-recursively saturated. Furthermore, we show that if the cohesive set is assumed to be co-c.e., then we obtain the
$\Sigma _n$
-recursively saturated. Furthermore, we show that if the cohesive set is assumed to be co-c.e., then we obtain the
![]() $n=0$
case and can also squeeze one more level of saturation out of the cohesive product: cohesive products of uniformly n-decidable structures over co-c.e. cohesive sets are always
$n=0$
case and can also squeeze one more level of saturation out of the cohesive product: cohesive products of uniformly n-decidable structures over co-c.e. cohesive sets are always
![]() $\Sigma _{n+1}$
-recursively saturated.
$\Sigma _{n+1}$
-recursively saturated.
We follow the terminology of [Reference Kaye15, Section 11.2] regarding types and saturation. Beware that what we call a type over a structure
![]() $\mathcal {A}$
, other authors may call a type over a finite set
$\mathcal {A}$
, other authors may call a type over a finite set
![]() $\{c_0, \dots , c_{\ell -1}\}$
of parameters from
$\{c_0, \dots , c_{\ell -1}\}$
of parameters from
![]() $\mathcal {A}$
. Let
$\mathcal {A}$
. Let
![]() $\mathfrak {L}$
be a language, and let
$\mathfrak {L}$
be a language, and let
![]() $\mathcal {A}$
be an
$\mathcal {A}$
be an
![]() $\mathfrak {L}$
-structure. Consider a set
$\mathfrak {L}$
-structure. Consider a set
![]() $p(\vec {x}) = p(x_0, \dots , x_{m-1})$
of formulas of the form
$p(\vec {x}) = p(x_0, \dots , x_{m-1})$
of formulas of the form
![]() $\Phi (\vec {x}; \vec {c}) = \Phi (x_0, \dots , x_{m-1}; c_0, \dots , c_{\ell -1})$
in the language
$\Phi (\vec {x}; \vec {c}) = \Phi (x_0, \dots , x_{m-1}; c_0, \dots , c_{\ell -1})$
in the language
![]() $\mathfrak {L} \cup \{c_0, \dots , c_{\ell -1}\}$
, where
$\mathfrak {L} \cup \{c_0, \dots , c_{\ell -1}\}$
, where
![]() $x_0, \dots , x_{m-1}$
are m fixed variables and
$x_0, \dots , x_{m-1}$
are m fixed variables and
![]() $c_0, \dots , c_{\ell -1}$
are
$c_0, \dots , c_{\ell -1}$
are
![]() $\ell $
fixed parameters from
$\ell $
fixed parameters from
![]() $|\mathcal {A}|$
that are identified with fresh constant symbols. Such a set
$|\mathcal {A}|$
that are identified with fresh constant symbols. Such a set
![]() $p(\vec {x})$
is called a type over
$p(\vec {x})$
is called a type over
![]() $\mathcal {A}$
if it is finitely satisfied in
$\mathcal {A}$
if it is finitely satisfied in
![]() $\mathcal {A}$
: for every
$\mathcal {A}$
: for every
![]() $\Phi _0(\vec {x}; \vec {c}), \dots , \Phi _{k-1}(\vec {x}; \vec {c}) \in p(\vec {x})$
,
$\Phi _0(\vec {x}; \vec {c}), \dots , \Phi _{k-1}(\vec {x}; \vec {c}) \in p(\vec {x})$
,
![]() $\mathcal {A} \models \exists \vec {x} \, \bigwedge _{i < k} \Phi _i(\vec {x}; \vec {c})$
. A type
$\mathcal {A} \models \exists \vec {x} \, \bigwedge _{i < k} \Phi _i(\vec {x}; \vec {c})$
. A type
![]() $p(\vec {x})$
over
$p(\vec {x})$
over
![]() $\mathcal {A}$
is realized if there are
$\mathcal {A}$
is realized if there are
![]() $a_0, \dots , a_{m-1} \in |\mathcal {A}|$
such that for all
$a_0, \dots , a_{m-1} \in |\mathcal {A}|$
such that for all
![]() $\Phi (\vec {x}; \vec {c}) \in p(\vec {x})$
,
$\Phi (\vec {x}; \vec {c}) \in p(\vec {x})$
,
![]() $\mathcal {A} \models \Phi (\vec {a}; \vec {c})$
. A type
$\mathcal {A} \models \Phi (\vec {a}; \vec {c})$
. A type
![]() $p(\vec {x})$
over
$p(\vec {x})$
over
![]() $\mathcal {A}$
is a
$\mathcal {A}$
is a
![]() $\Sigma _n$
-type if every formula in
$\Sigma _n$
-type if every formula in
![]() $p(\vec {x})$
is
$p(\vec {x})$
is
![]() $\Sigma _n$
. An
$\Sigma _n$
. An
![]() $\mathfrak {L}$
-structure
$\mathfrak {L}$
-structure
![]() $\mathcal {A}$
is recursively saturated if it realizes every computable type over
$\mathcal {A}$
is recursively saturated if it realizes every computable type over
![]() $\mathcal {A}$
. Similarly,
$\mathcal {A}$
. Similarly,
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\Sigma _n$
-recursively saturated if it realizes every computable
$\Sigma _n$
-recursively saturated if it realizes every computable
![]() $\Sigma _n$
-type over
$\Sigma _n$
-type over
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
When discussing a formula
![]() $\Phi (\vec {x}; \vec {c})$
of a type
$\Phi (\vec {x}; \vec {c})$
of a type
![]() $p(\vec {x})$
, we write
$p(\vec {x})$
, we write
![]() $\Phi (\vec {x}; \vec {y})$
for the corresponding
$\Phi (\vec {x}; \vec {y})$
for the corresponding
![]() $\mathfrak {L}$
-formula, with fresh variables
$\mathfrak {L}$
-formula, with fresh variables
![]() $\vec {y}$
in place of the constants
$\vec {y}$
in place of the constants
![]() $\vec {c}$
. We sometimes write
$\vec {c}$
. We sometimes write
![]() $p(\vec {x}; \vec {c})$
or
$p(\vec {x}; \vec {c})$
or
![]() $p(\vec {x}; \vec {y})$
in place of
$p(\vec {x}; \vec {y})$
in place of
![]() $p(\vec {x})$
when we want to emphasize the type’s parameters or the corresponding variables.
$p(\vec {x})$
when we want to emphasize the type’s parameters or the corresponding variables.
Lemma 2.15. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
$(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
![]() $\mathfrak {L}$
-structures, and let C be cohesive. Let
$\mathfrak {L}$
-structures, and let C be cohesive. Let
![]() $p(\vec {x}; \vec {c})$
be a computable type over
$p(\vec {x}; \vec {c})$
be a computable type over
![]() $\prod _C \mathcal {A}_n$
with computable enumeration
$\prod _C \mathcal {A}_n$
with computable enumeration
![]() $(\Phi _i : i \in \mathbb {N})$
. Assume that the formulas
$(\Phi _i : i \in \mathbb {N})$
. Assume that the formulas
 $$ \begin{align*} \left(\exists \vec{x}\; \bigwedge_{i < k} \Phi_i(\vec{x}; \vec{y}) : k \in \mathbb{N}\right) \end{align*} $$
$$ \begin{align*} \left(\exists \vec{x}\; \bigwedge_{i < k} \Phi_i(\vec{x}; \vec{y}) : k \in \mathbb{N}\right) \end{align*} $$
are uniformly decidable in the structures
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
. Then
$(\mathcal {A}_n : n \in \mathbb {N})$
. Then
![]() $\prod _C \mathcal {A}_n$
realizes
$\prod _C \mathcal {A}_n$
realizes
![]() $p(\vec {x}; \vec {c})$
.
$p(\vec {x}; \vec {c})$
.
Proof Let
![]() $\vec {c} = [\psi _0], \dots , [\psi _{\ell -1}]$
be the parameters of the type
$\vec {c} = [\psi _0], \dots , [\psi _{\ell -1}]$
be the parameters of the type
![]() $p(\vec {x}; \vec {c})$
, so that
$p(\vec {x}; \vec {c})$
, so that
for each k. To ease notation, pack
![]() $\psi _0, \dots , \psi _{\ell -1}$
into a single partial computable function
$\psi _0, \dots , \psi _{\ell -1}$
into a single partial computable function
![]() $\psi \colon \mathbb {N} \rightarrow \mathbb {N}^\ell $
given by
$\psi \colon \mathbb {N} \rightarrow \mathbb {N}^\ell $
given by
![]() $\psi (n) \simeq \langle \psi _0(n), \dots , \psi _{\ell -1}(n) \rangle $
. Notice that
$\psi (n) \simeq \langle \psi _0(n), \dots , \psi _{\ell -1}(n) \rangle $
. Notice that
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\psi )$
. Write
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\psi )$
. Write
![]() $\overrightarrow {[\psi ]}$
as an abbreviation for
$\overrightarrow {[\psi ]}$
as an abbreviation for
![]() $[\psi _0], \dots , [\psi _{\ell -1}]$
.
$[\psi _0], \dots , [\psi _{\ell -1}]$
.
Define a partial computable function
![]() $\varphi \colon \mathbb {N} \rightarrow \mathbb {N}^m$
as follows. Given n, first search for the greatest
$\varphi \colon \mathbb {N} \rightarrow \mathbb {N}^m$
as follows. Given n, first search for the greatest
![]() $k \leq n$
such that
$k \leq n$
such that
This search is effective on account of the uniform decidability assumption. If such a k is found, search for the first tuple
![]() $\vec {a} = \langle a_0, \dots , a_{m-1} \rangle $
such that
$\vec {a} = \langle a_0, \dots , a_{m-1} \rangle $
such that
![]() $\mathcal {A}_n \models \bigwedge _{i < k} \Phi _i(\vec {a}; \psi (n))$
, and set
$\mathcal {A}_n \models \bigwedge _{i < k} \Phi _i(\vec {a}; \psi (n))$
, and set
![]() $\varphi (n) = \vec {a}$
. If there is no such k, then
$\varphi (n) = \vec {a}$
. If there is no such k, then
![]() $\varphi (n){\uparrow }$
.
$\varphi (n){\uparrow }$
.
Consider a fixed k. By assumption,
![]() $\prod _C \mathcal {A}_n \models \exists \vec {x}\; \bigwedge _{i < k} \Phi _i\left (\vec {x}; \overrightarrow {[\psi ]}\right )$
. Thus
$\prod _C \mathcal {A}_n \models \exists \vec {x}\; \bigwedge _{i < k} \Phi _i\left (\vec {x}; \overrightarrow {[\psi ]}\right )$
. Thus
![]() $C \subseteq ^* \bigl \{n : \mathcal {A}_n \models \exists \vec {x}\, \bigwedge _{i < k} \Phi _i(\vec {x}; \psi (n))\bigr \}$
by Lemma 2.4. This means that for almost every
$C \subseteq ^* \bigl \{n : \mathcal {A}_n \models \exists \vec {x}\, \bigwedge _{i < k} \Phi _i(\vec {x}; \psi (n))\bigr \}$
by Lemma 2.4. This means that for almost every
![]() $n \in C$
with
$n \in C$
with
![]() $n \geq k$
, the initial search in the computation of
$n \geq k$
, the initial search in the computation of
![]() $\varphi (n)$
succeeds and finds a
$\varphi (n)$
succeeds and finds a
![]() $\widehat {k}$
with
$\widehat {k}$
with
![]() $k \leq \widehat {k} \leq n$
. Thus
$k \leq \widehat {k} \leq n$
. Thus
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
and
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
and
 $$ \begin{align*} C \subseteq^* \left\{n : \mathcal{A}_n \models \bigwedge_{i < k} \Phi_i(\varphi(n); \psi(n))\right\}. \end{align*} $$
$$ \begin{align*} C \subseteq^* \left\{n : \mathcal{A}_n \models \bigwedge_{i < k} \Phi_i(\varphi(n); \psi(n))\right\}. \end{align*} $$
Let
![]() $\varphi _i = \pi _i \circ \varphi $
for each
$\varphi _i = \pi _i \circ \varphi $
for each
![]() $i < m$
. Then
$i < m$
. Then
![]() $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
. Let
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
. Let
![]() $\overrightarrow {[\varphi ]}$
abbreviate the sequence
$\overrightarrow {[\varphi ]}$
abbreviate the sequence
![]() $[\varphi _0], \dots , [\varphi _{m-1}]$
. Then
$[\varphi _0], \dots , [\varphi _{m-1}]$
. Then
![]() $\prod _C \mathcal {A}_n \models \bigwedge _{i < k} \Phi _i \left (\overrightarrow {[\varphi ]}; \overrightarrow {[\psi ]}\right )$
by Lemma 2.4. This implies that
$\prod _C \mathcal {A}_n \models \bigwedge _{i < k} \Phi _i \left (\overrightarrow {[\varphi ]}; \overrightarrow {[\psi ]}\right )$
by Lemma 2.4. This implies that
![]() $\prod _C \mathcal {A}_n \models \Phi _i \left (\overrightarrow {[\varphi ]}; \overrightarrow {[\psi ]}\right )$
for every i. Thus
$\prod _C \mathcal {A}_n \models \Phi _i \left (\overrightarrow {[\varphi ]}; \overrightarrow {[\psi ]}\right )$
for every i. Thus
![]() $[\varphi _0], \dots , [\varphi _{m-1}]$
realize
$[\varphi _0], \dots , [\varphi _{m-1}]$
realize
![]() $p(\vec {x}; \overrightarrow {[\psi ]})$
in
$p(\vec {x}; \overrightarrow {[\psi ]})$
in
![]() $\prod _C \mathcal {A}_n$
.
$\prod _C \mathcal {A}_n$
.
Items (1) and (3) of the next theorem are essentially [Reference Nelson20, Theorem 2.2].
Theorem 2.16. Let
![]() $\mathfrak {L}$
be a computable language, and let C be a cohesive set.
$\mathfrak {L}$
be a computable language, and let C be a cohesive set.
-
(1) Let
 $(\mathcal {A}_i : i \in \mathbb {N})$
be a sequence of uniformly decidable
$(\mathcal {A}_i : i \in \mathbb {N})$
be a sequence of uniformly decidable
 $\mathfrak {L}$
-structures. Then
$\mathfrak {L}$
-structures. Then
 $\prod _C \mathcal {A}_i$
is recursively saturated.
$\prod _C \mathcal {A}_i$
is recursively saturated. -
(2) Let
 $(\mathcal {A}_i : i \in \mathbb {N})$
be a sequence of uniformly n-decidable
$(\mathcal {A}_i : i \in \mathbb {N})$
be a sequence of uniformly n-decidable
 $\mathfrak {L}$
-structures for an
$\mathfrak {L}$
-structures for an
 $n> 0$
. Then
$n> 0$
. Then
 $\prod _C \mathcal {A}_i$
is
$\prod _C \mathcal {A}_i$
is
 $\Sigma _n$
-recursively saturated.
$\Sigma _n$
-recursively saturated. -
(3) Let
 $\mathcal {A}$
be a decidable
$\mathcal {A}$
be a decidable
 $\mathfrak {L}$
-structure. Then
$\mathfrak {L}$
-structure. Then
 $\prod _C \mathcal {A}$
is recursively saturated.
$\prod _C \mathcal {A}$
is recursively saturated. -
(4) Let
 $\mathcal {A}$
be an n-decidable
$\mathcal {A}$
be an n-decidable
 $\mathfrak {L}$
-structure for an
$\mathfrak {L}$
-structure for an
 $n> 0$
. Then
$n> 0$
. Then
 $\prod _C \mathcal {A}$
is
$\prod _C \mathcal {A}$
is
 $\Sigma _n$
-recursively saturated.
$\Sigma _n$
-recursively saturated.
Proof Item (1) follows directly from Lemma 2.15 because every computably enumerable sequence of formulas is uniformly decidable in
![]() $(\mathcal {A}_i : i \in \mathbb {N})$
. Item (2) also follows from Lemma 2.15. If
$(\mathcal {A}_i : i \in \mathbb {N})$
. Item (2) also follows from Lemma 2.15. If
![]() $(\Phi _i : i \in \mathbb {N})$
is a computable enumeration of
$(\Phi _i : i \in \mathbb {N})$
is a computable enumeration of
![]() $\Sigma _n$
formulas and
$\Sigma _n$
formulas and
![]() $n> 0$
, then
$n> 0$
, then
 $$ \begin{align*} \left(\exists \vec{x}\; \bigwedge_{i < k} \Phi_i(\vec{x}; \vec{y}) : k \in \mathbb{N}\right) \end{align*} $$
$$ \begin{align*} \left(\exists \vec{x}\; \bigwedge_{i < k} \Phi_i(\vec{x}; \vec{y}) : k \in \mathbb{N}\right) \end{align*} $$
is a computable enumeration of (formulas that are logically equivalent to)
![]() $\Sigma _n$
formulas and hence is uniformly decidable in
$\Sigma _n$
formulas and hence is uniformly decidable in
![]() $(\mathcal {A}_i : i \in \mathbb {N})$
. Items (3) and (4) are the special cases of items (1) and (2) in which
$(\mathcal {A}_i : i \in \mathbb {N})$
. Items (3) and (4) are the special cases of items (1) and (2) in which
![]() $\mathcal {A}_i$
is
$\mathcal {A}_i$
is
![]() $\mathcal {A}$
for each i.
$\mathcal {A}$
for each i.
If we restrict to co-c.e. cohesive sets, then we can include
![]() $n=0$
and improve
$n=0$
and improve
![]() $\Sigma _n$
-recursive saturation to
$\Sigma _n$
-recursive saturation to
![]() $\Sigma _{n+1}$
-recursive saturation in Theorem 2.16 items (2) and (4).
$\Sigma _{n+1}$
-recursive saturation in Theorem 2.16 items (2) and (4).
Lemma 2.17. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
$(\mathcal {A}_n : n \in \mathbb {N})$
be a uniformly computable sequence of
![]() $\mathfrak {L}$
-structures, and let C be co-c.e. and cohesive. Let
$\mathfrak {L}$
-structures, and let C be co-c.e. and cohesive. Let
![]() $p(\vec {x}; \vec {c})$
be a computable type over
$p(\vec {x}; \vec {c})$
be a computable type over
![]() $\prod _C \mathcal {A}_n$
consisting of formulas of the form
$\prod _C \mathcal {A}_n$
consisting of formulas of the form
![]() $\exists \vec {z}\, \Phi (\vec {x}, \vec {z}; \vec {c})$
, with computable enumeration
$\exists \vec {z}\, \Phi (\vec {x}, \vec {z}; \vec {c})$
, with computable enumeration
![]() $(\exists \vec {z}_i\, \Phi _i(\vec {x}, \vec {z}_i; \vec {c}) : i \in \mathbb {N})$
. Further assume that the formulas
$(\exists \vec {z}_i\, \Phi _i(\vec {x}, \vec {z}_i; \vec {c}) : i \in \mathbb {N})$
. Further assume that the formulas
![]() $(\Phi _i(\vec {x}, \vec {z}_i; \vec {y}) : i \in \mathbb {N})$
are uniformly decidable in the structures
$(\Phi _i(\vec {x}, \vec {z}_i; \vec {y}) : i \in \mathbb {N})$
are uniformly decidable in the structures
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
. Then
$(\mathcal {A}_n : n \in \mathbb {N})$
. Then
![]() $\prod _C \mathcal {A}_n$
realizes
$\prod _C \mathcal {A}_n$
realizes
![]() $p(\vec {x}; \vec {c})$
.
$p(\vec {x}; \vec {c})$
.
Proof Let
![]() $\vec {c} = [\psi _0], \dots , [\psi _{\ell -1}]$
be the parameters of the type
$\vec {c} = [\psi _0], \dots , [\psi _{\ell -1}]$
be the parameters of the type
![]() $p(\vec {x}; \vec {c})$
, so that
$p(\vec {x}; \vec {c})$
, so that
for each k. As in the proof of Lemma 2.15, let
![]() $\psi \colon \mathbb {N} \rightarrow \mathbb {N}^\ell $
be the partial computable function given by
$\psi \colon \mathbb {N} \rightarrow \mathbb {N}^\ell $
be the partial computable function given by
![]() $\psi (n) \simeq \langle \psi _0(n), \dots , \psi _{\ell -1}(n) \rangle $
. Notice that
$\psi (n) \simeq \langle \psi _0(n), \dots , \psi _{\ell -1}(n) \rangle $
. Notice that
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\psi )$
, and write
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\psi )$
, and write
![]() $\overrightarrow {[\psi ]}$
as an abbreviation for
$\overrightarrow {[\psi ]}$
as an abbreviation for
![]() $[\psi _0], \dots , [\psi _{\ell -1}]$
.
$[\psi _0], \dots , [\psi _{\ell -1}]$
.
The goal is to partially compute a function
![]() $\theta \colon \mathbb {N} \rightarrow \mathbb {N}^m$
so that
$\theta \colon \mathbb {N} \rightarrow \mathbb {N}^m$
so that
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
and
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
and
for each i. The set
is c.e. for each i because
![]() $\Phi _i$
is uniformly decidable in
$\Phi _i$
is uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
. Thus (*) implies that
$(\mathcal {A}_n : n \in \mathbb {N})$
. Thus (*) implies that
for each i by cohesiveness. Letting
![]() $\varphi _j = \pi _j \circ \theta $
for each
$\varphi _j = \pi _j \circ \theta $
for each
![]() $j < m$
, we therefore have that
$j < m$
, we therefore have that
![]() $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
and that
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}_n|$
and that
for each i by Lemma 2.6. Thus
![]() $[\varphi _0], \dots , [\varphi _{m-1}]$
realize
$[\varphi _0], \dots , [\varphi _{m-1}]$
realize
![]() $p(\vec {x}; \overrightarrow {[\psi ]})$
in
$p(\vec {x}; \overrightarrow {[\psi ]})$
in
![]() $\prod _C \mathcal {A}_n$
.
$\prod _C \mathcal {A}_n$
.
The strategy for partially computing
![]() $\theta $
is to keep track of the numbers k that are covered, meaning that it looks like there is an
$\theta $
is to keep track of the numbers k that are covered, meaning that it looks like there is an
![]() $n \in C$
with
$n \in C$
with
![]() $n> k$
such that
$n> k$
such that
![]() $\mathcal {A}_n \models \bigwedge _{i < k} \exists \vec {z}_i\, \Phi _i(\theta (n), \vec {z}_i; \psi (n))$
. As the computation progresses, a k that is covered may become uncovered because the n that covers it is enumerated in the complement of C. When this happens, we note the least k that becomes uncovered, we search for the first
$\mathcal {A}_n \models \bigwedge _{i < k} \exists \vec {z}_i\, \Phi _i(\theta (n), \vec {z}_i; \psi (n))$
. As the computation progresses, a k that is covered may become uncovered because the n that covers it is enumerated in the complement of C. When this happens, we note the least k that becomes uncovered, we search for the first
![]() $n> k$
where
$n> k$
where
![]() $\theta (n)$
is not yet defined, it looks like
$\theta (n)$
is not yet defined, it looks like
![]() $n \in C$
, and there looks to be an
$n \in C$
, and there looks to be an
![]() $\vec {a} \in \mathbb {N}^m$
such that
$\vec {a} \in \mathbb {N}^m$
such that
![]() $\mathcal {A}_n \models \bigwedge _{i < k} \exists \vec {z}_i\, \Phi _i(\vec {a}, \vec {z}_i; \psi (n))$
, and we attempt to cover k again by setting
$\mathcal {A}_n \models \bigwedge _{i < k} \exists \vec {z}_i\, \Phi _i(\vec {a}, \vec {z}_i; \psi (n))$
, and we attempt to cover k again by setting
![]() $\theta (n) = \vec {a}$
. This strategy eventually succeeds because if
$\theta (n) = \vec {a}$
. This strategy eventually succeeds because if
![]() $n_0 \in C$
is sufficiently large and we never choose a smaller member of C to cover k, then we eventually choose
$n_0 \in C$
is sufficiently large and we never choose a smaller member of C to cover k, then we eventually choose
![]() $n_0$
to cover either k or an even bigger number.
$n_0$
to cover either k or an even bigger number.
Formally, let W denote the c.e. set
![]() $\overline {C}$
, and let
$\overline {C}$
, and let
![]() $(W_s)_{s \in \mathbb {N}}$
be a computable
$(W_s)_{s \in \mathbb {N}}$
be a computable
![]() $\subseteq $
-increasing enumeration of W. Let
$\subseteq $
-increasing enumeration of W. Let
![]() $(U_k : k \in \mathbb {N})$
be the uniformly c.e. sequence of sets given by
$(U_k : k \in \mathbb {N})$
be the uniformly c.e. sequence of sets given by
 $$ \begin{align*} U_k = \left\{\langle \vec{a}, n \rangle \in \mathbb{N}^m \times \mathbb{N}: \mathcal{A}_n \models \bigwedge_{i < k} \exists \vec{z}_i\, \Phi_i(\vec{a}, \vec{z}_i; \psi(n))\right\} \end{align*} $$
$$ \begin{align*} U_k = \left\{\langle \vec{a}, n \rangle \in \mathbb{N}^m \times \mathbb{N}: \mathcal{A}_n \models \bigwedge_{i < k} \exists \vec{z}_i\, \Phi_i(\vec{a}, \vec{z}_i; \psi(n))\right\} \end{align*} $$
with uniformly computable
![]() $\subseteq $
-increasing enumerations
$\subseteq $
-increasing enumerations
![]() $(U_{k,s})_{s \in \mathbb {N}}$
for each k. The sequence
$(U_{k,s})_{s \in \mathbb {N}}$
for each k. The sequence
![]() $(U_k : k \in \mathbb {N})$
is uniformly c.e. because the formulas
$(U_k : k \in \mathbb {N})$
is uniformly c.e. because the formulas
![]() $(\Phi _i : i \in \mathbb {N})$
are uniformly decidable in
$(\Phi _i : i \in \mathbb {N})$
are uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
. Observe that if
$(\mathcal {A}_n : n \in \mathbb {N})$
. Observe that if
![]() $k_0 \leq k_1$
, then
$k_0 \leq k_1$
, then
![]() $U_{k_1} \subseteq U_{k_0}$
.
$U_{k_1} \subseteq U_{k_0}$
.
To partially compute
![]() $\theta $
, we compute an increasing sequence
$\theta $
, we compute an increasing sequence
![]() $\theta _0 \subseteq \theta _1 \subseteq \theta _2 \subseteq \ldots $
of finite approximations to
$\theta _0 \subseteq \theta _1 \subseteq \theta _2 \subseteq \ldots $
of finite approximations to
![]() $\theta $
. Start at stage
$\theta $
. Start at stage
![]() $0$
with
$0$
with
![]() $\theta _0 = \emptyset $
. At stage s, we have
$\theta _0 = \emptyset $
. At stage s, we have
![]() $\theta _s$
and we define
$\theta _s$
and we define
![]() $\theta _{s+1}$
.
$\theta _{s+1}$
.
Say that n covers k at stage s if:
-
•
 $n> k$
,
$n> k$
, -
•
 $n \notin W_s$
,
$n \notin W_s$
, -
•
 $\theta _s(n){\downarrow }$
, and
$\theta _s(n){\downarrow }$
, and -
•
 $\langle \theta _s(n), n \rangle \in U_{k,s}$
.
$\langle \theta _s(n), n \rangle \in U_{k,s}$
.
If there is an n that covers k at stage s, then also say that k is covered at stage s. Let
![]() $k^0_s$
be the least number that is not covered at stage s. If
$k^0_s$
be the least number that is not covered at stage s. If
![]() $s> 0$
, let
$s> 0$
, let
![]() $X_s = W_s \setminus W_{s-1}$
. Let
$X_s = W_s \setminus W_{s-1}$
. Let
![]() $k^1_s$
be the least number, if it exists, for which some
$k^1_s$
be the least number, if it exists, for which some
![]() $n \in X_s$
covered
$n \in X_s$
covered
![]() $k^1_s$
at stage
$k^1_s$
at stage
![]() $s-1$
but no
$s-1$
but no
![]() $m < n$
covers
$m < n$
covers
![]() $k^1_s$
at stage s. If
$k^1_s$
at stage s. If
![]() $k^1_s$
is defined, let
$k^1_s$
is defined, let
![]() $k_s = \min \{k^0_s, k^1_s\}$
. Otherwise, let
$k_s = \min \{k^0_s, k^1_s\}$
. Otherwise, let
![]() $k_s = k^0_s$
. Now search for the least
$k_s = k^0_s$
. Now search for the least
![]() $n> k_s$
such that
$n> k_s$
such that
![]() $n \notin W_s$
, such that
$n \notin W_s$
, such that
![]() $\theta _s(n){\uparrow }$
, and such that
$\theta _s(n){\uparrow }$
, and such that
![]() $\langle \vec {a}, n \rangle \in U_{k_s, s}$
for some
$\langle \vec {a}, n \rangle \in U_{k_s, s}$
for some
![]() $\vec {a}$
. If there is such an n, let
$\vec {a}$
. If there is such an n, let
![]() $\vec {a}$
be the first corresponding
$\vec {a}$
be the first corresponding
![]() $\vec {a}$
, and extend
$\vec {a}$
, and extend
![]() $\theta _s$
to
$\theta _s$
to
![]() $\theta _{s+1}$
by setting
$\theta _{s+1}$
by setting
![]() $\theta _{s+1}(n) = \vec {a}$
. If there is no such n, then set
$\theta _{s+1}(n) = \vec {a}$
. If there is no such n, then set
![]() $\theta _{s+1} = \theta _s$
. Go to stage
$\theta _{s+1} = \theta _s$
. Go to stage
![]() $s+1$
. This completes the partial computation of
$s+1$
. This completes the partial computation of
![]() $\theta $
.
$\theta $
.
If n covers k at some stage s, there could be a later stage
![]() $t> s$
at which n does not cover k because
$t> s$
at which n does not cover k because
![]() $n \in W_t$
. However, if
$n \in W_t$
. However, if
![]() $n \in C$
, then
$n \in C$
, then
![]() $n \notin W_t$
for every t, so k stays covered by n forever.
$n \notin W_t$
for every t, so k stays covered by n forever.
Claim. Every k is eventually covered by an
![]() $n \in C$
.
$n \in C$
.
Proof of Claim
Proceed by induction on k. Let
![]() $s_0$
be a stage by which all
$s_0$
be a stage by which all
![]() $\widehat {k} < k$
have been covered by members of C. Let c be the greatest member of C covering a
$\widehat {k} < k$
have been covered by members of C. Let c be the greatest member of C covering a
![]() $\widehat {k} < k$
at stage
$\widehat {k} < k$
at stage
![]() $s_0$
, and let
$s_0$
, and let
![]() $s_1> s_0$
be a stage such that
$s_1> s_0$
be a stage such that
![]() $W_{s_1} {\restriction } c = W {\restriction } c$
. Then
$W_{s_1} {\restriction } c = W {\restriction } c$
. Then
![]() $k_s \geq k$
at all stages
$k_s \geq k$
at all stages
![]() $s> s_1$
. By assumption,
$s> s_1$
. By assumption,
 $$ \begin{align*} \prod\nolimits_C \mathcal{A}_n \models \exists \vec{x}\, \bigwedge_{i < k} \exists \vec{z}_i\, \Phi_i\left(\vec{x}, \vec{z}_i; \overrightarrow{[\psi]} \right), \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathcal{A}_n \models \exists \vec{x}\, \bigwedge_{i < k} \exists \vec{z}_i\, \Phi_i\left(\vec{x}, \vec{z}_i; \overrightarrow{[\psi]} \right), \end{align*} $$
and therefore
 $$ \begin{align*} C \subseteq^* \left\{n : \mathcal{A}_n \models \exists \vec{x}\, \bigwedge_{i < k} \exists \vec{z}_i\, \Phi_i\left(\vec{x}, \vec{z}_i; \psi(n) \right)\right\} \end{align*} $$
$$ \begin{align*} C \subseteq^* \left\{n : \mathcal{A}_n \models \exists \vec{x}\, \bigwedge_{i < k} \exists \vec{z}_i\, \Phi_i\left(\vec{x}, \vec{z}_i; \psi(n) \right)\right\} \end{align*} $$
by Lemma 2.6. To see that Lemma 2.6 applies here, pull the
![]() $\exists \vec {z}_i$
quantifiers out in front of the conjunction. The resulting formula has the form
$\exists \vec {z}_i$
quantifiers out in front of the conjunction. The resulting formula has the form
![]() $\exists \vec {w}\, \Psi (\vec {w}; \vec {y})$
, where
$\exists \vec {w}\, \Psi (\vec {w}; \vec {y})$
, where
![]() $\Psi $
is uniformly decidable in
$\Psi $
is uniformly decidable in
![]() $(\mathcal {A}_n : n \in \mathbb {N})$
. Let
$(\mathcal {A}_n : n \in \mathbb {N})$
. Let
![]() $n_0$
be least such that
$n_0$
be least such that
![]() $n_0> k$
, such that
$n_0> k$
, such that
![]() $n_0 \in C$
, such that
$n_0 \in C$
, such that
![]() $\theta _{s_1}(n_0){\uparrow }$
, such that
$\theta _{s_1}(n_0){\uparrow }$
, such that
![]() $\psi (n_0){\downarrow }$
, and such that
$\psi (n_0){\downarrow }$
, and such that
If
![]() $\theta _s(n_0){\downarrow }$
for the first time at some stage
$\theta _s(n_0){\downarrow }$
for the first time at some stage
![]() $s> s_1$
, it is to cover some
$s> s_1$
, it is to cover some
![]() $j \geq k$
. As
$j \geq k$
. As
![]() $n_0 \in C$
, we have that
$n_0 \in C$
, we have that
![]() $n_0$
covers j and therefore covers k at all later stages.
$n_0$
covers j and therefore covers k at all later stages.
Let
![]() $s_2> s_1$
be large enough so that
$s_2> s_1$
be large enough so that
![]() $W_{s_2} {\restriction } n_0 = W {\restriction } n_0$
and so that there is an
$W_{s_2} {\restriction } n_0 = W {\restriction } n_0$
and so that there is an
![]() $\vec {a}$
with
$\vec {a}$
with
![]() $\langle \vec {a}, n_0 \rangle \in U_{k, s_2}$
. Consider stage
$\langle \vec {a}, n_0 \rangle \in U_{k, s_2}$
. Consider stage
![]() $s_2$
. If k is not covered at stage
$s_2$
. If k is not covered at stage
![]() $s_2$
, then it must be that
$s_2$
, then it must be that
![]() $\theta _{s_2}(n_0){\uparrow }$
. In this case,
$\theta _{s_2}(n_0){\uparrow }$
. In this case,
![]() $k_{s_2} = k$
, and
$k_{s_2} = k$
, and
![]() $n_0$
is least such that
$n_0$
is least such that
![]() $n_0> k_{s_2}$
,
$n_0> k_{s_2}$
,
![]() $n_0 \notin W_{s_2}$
,
$n_0 \notin W_{s_2}$
,
![]() $\theta _{s_2}(n_0){\uparrow }$
, and
$\theta _{s_2}(n_0){\uparrow }$
, and
![]() $\langle \vec {a}, n_0 \rangle \in U_{k_{s_2}, s_2}$
for some
$\langle \vec {a}, n_0 \rangle \in U_{k_{s_2}, s_2}$
for some
![]() $\vec {a}$
. So
$\vec {a}$
. So
![]() $\theta _{s_2 + 1}(n_0)$
is defined to cover k at stage
$\theta _{s_2 + 1}(n_0)$
is defined to cover k at stage
![]() $s_2$
.
$s_2$
.
Suppose instead that k is covered at stage
![]() $s_2$
. In this case, let
$s_2$
. In this case, let
![]() $n_1$
be least such that there is a stage
$n_1$
be least such that there is a stage
![]() $s_3 \geq s_2$
at which
$s_3 \geq s_2$
at which
![]() $n_1$
covers k. If
$n_1$
covers k. If
![]() $n_1 \in C$
, then this is as desired. Otherwise,
$n_1 \in C$
, then this is as desired. Otherwise,
![]() $n_1 \in W$
, in which case there is a least
$n_1 \in W$
, in which case there is a least
![]() $s> s_3$
with
$s> s_3$
with
![]() $n_1 \in W_s$
. The number
$n_1 \in W_s$
. The number
![]() $n_1$
covers k at stage
$n_1$
covers k at stage
![]() $s-1$
, but by choice of
$s-1$
, but by choice of
![]() $n_1$
, no
$n_1$
, no
![]() $n < n_1$
covers k at stage s. Thus
$n < n_1$
covers k at stage s. Thus
![]() $k^1_s = k$
, so
$k^1_s = k$
, so
![]() $k_s = k$
. If
$k_s = k$
. If
![]() $\theta _s(n_0){\downarrow }$
, then
$\theta _s(n_0){\downarrow }$
, then
![]() $n_0$
must already cover k, as noted above. If
$n_0$
must already cover k, as noted above. If
![]() $\theta _s(n_0){\uparrow }$
, then
$\theta _s(n_0){\uparrow }$
, then
![]() $n_0$
is least such that
$n_0$
is least such that
![]() $n_0> k_s$
,
$n_0> k_s$
,
![]() $n_0 \notin W_s$
,
$n_0 \notin W_s$
,
![]() $\theta _s(n_0){\uparrow }$
, and
$\theta _s(n_0){\uparrow }$
, and
![]() $\langle \vec {a}, n_0 \rangle \in U_{k_s, s}$
for some
$\langle \vec {a}, n_0 \rangle \in U_{k_s, s}$
for some
![]() $\vec {a}$
. So
$\vec {a}$
. So
![]() $\theta _{s+1}(n_0)$
is defined to cover k at stage s. This completes the proof of the claim.
$\theta _{s+1}(n_0)$
is defined to cover k at stage s. This completes the proof of the claim.
To finish the proof, consider the formula
![]() $\exists \vec {z}_i\, \Phi _i$
. By the claim, every k is eventually covered by an
$\exists \vec {z}_i\, \Phi _i$
. By the claim, every k is eventually covered by an
![]() $n \in C$
. Thus for every
$n \in C$
. Thus for every
![]() $k> i$
, there is an
$k> i$
, there is an
![]() $n> k$
with
$n> k$
with
![]() $n \in C$
,
$n \in C$
,
![]() $\theta (n){\downarrow }$
, and
$\theta (n){\downarrow }$
, and
![]() $\langle \theta (n), n \rangle \in U_k$
. Thus
$\langle \theta (n), n \rangle \in U_k$
. Thus
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
by cohesiveness, and
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
by cohesiveness, and
as desired.
Theorem 2.18. Let
![]() $\mathfrak {L}$
be a computable language, and let C be a co-c.e. cohesive set.
$\mathfrak {L}$
be a computable language, and let C be a co-c.e. cohesive set.
-
(1) Let
 $(\mathcal {A}_i : i \in \mathbb {N})$
be a sequence of uniformly n-decidable
$(\mathcal {A}_i : i \in \mathbb {N})$
be a sequence of uniformly n-decidable
 $\mathfrak {L}$
-structures. Then
$\mathfrak {L}$
-structures. Then
 $\prod _C \mathcal {A}_i$
is
$\prod _C \mathcal {A}_i$
is
 $\Sigma _{n+1}$
-recursively saturated.
$\Sigma _{n+1}$
-recursively saturated. -
(2) Let
 $\mathcal {A}$
be an n-decidable
$\mathcal {A}$
be an n-decidable
 $\mathfrak {L}$
-structure. Then
$\mathfrak {L}$
-structure. Then
 $\prod _C \mathcal {A}$
is
$\prod _C \mathcal {A}$
is
 $\Sigma _{n+1}$
-recursively saturated.
$\Sigma _{n+1}$
-recursively saturated.
Proof Item (1) follows from Lemma 2.17. A computable
![]() $\Sigma _{n+1}$
-type can be computably enumerated as
$\Sigma _{n+1}$
-type can be computably enumerated as
![]() $(\exists \vec {z}_j\, \Phi _j : j \in \mathbb {N})$
, where
$(\exists \vec {z}_j\, \Phi _j : j \in \mathbb {N})$
, where
![]() $\Phi _j$
is
$\Phi _j$
is
![]() $\Pi _n$
for every j. The formulas
$\Pi _n$
for every j. The formulas
![]() $(\Phi _j : j \in \mathbb {N})$
are then uniformly decidable in
$(\Phi _j : j \in \mathbb {N})$
are then uniformly decidable in
![]() $(\mathcal {A}_i : i \in \mathbb {N})$
because
$(\mathcal {A}_i : i \in \mathbb {N})$
because
![]() $(\mathcal {A}_i : i \in \mathbb {N})$
is a uniformly n-decidable sequence of structures. Item (2) is the special case of item (1) in which
$(\mathcal {A}_i : i \in \mathbb {N})$
is a uniformly n-decidable sequence of structures. Item (2) is the special case of item (1) in which
![]() $\mathcal {A}_i$
is
$\mathcal {A}_i$
is
![]() $\mathcal {A}$
for each i.
$\mathcal {A}$
for each i.
The
![]() $n=0$
case of Theorem 2.18 is particularly noteworthy.
$n=0$
case of Theorem 2.18 is particularly noteworthy.
Corollary 2.19. Let
![]() $\mathfrak {L}$
be a computable language, and let C be a co-c.e. cohesive set.
$\mathfrak {L}$
be a computable language, and let C be a co-c.e. cohesive set.
-
(1) Let
 $(\mathcal {A}_i : i \in \mathbb {N})$
be a uniformly computable sequence of
$(\mathcal {A}_i : i \in \mathbb {N})$
be a uniformly computable sequence of
 $\mathfrak {L}$
-structures. Then
$\mathfrak {L}$
-structures. Then
 $\prod _C \mathcal {A}_i$
is
$\prod _C \mathcal {A}_i$
is
 $\Sigma _1$
-recursively saturated.
$\Sigma _1$
-recursively saturated. -
(2) Let
 $\mathcal {A}$
be a computable
$\mathcal {A}$
be a computable
 $\mathfrak {L}$
-structure. Then
$\mathfrak {L}$
-structure. Then
 $\prod _C \mathcal {A}$
is
$\prod _C \mathcal {A}$
is
 $\Sigma _1$
-recursively saturated.
$\Sigma _1$
-recursively saturated.
2.5 Isomorphisms
Classically, an isomorphism between two structures induces an isomorphism between the corresponding ultrapowers over a fixed ultrafilter. In the effective case, a computable isomorphism between two computable structures induces an isomorphism between the corresponding cohesive powers over a fixed cohesive set. This fact essentially appears in [Reference Dimitrov4], but we include a proof here for completeness.
Theorem 2.20. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $\mathcal {A}_0$
and
$\mathcal {A}_0$
and
![]() $\mathcal {A}_1$
be computable
$\mathcal {A}_1$
be computable
![]() $\mathfrak {L}$
-structures that are computably isomorphic, and let C be cohesive. Then
$\mathfrak {L}$
-structures that are computably isomorphic, and let C be cohesive. Then
![]() $\prod _C \mathcal {A}_0 \cong \prod _C \mathcal {A}_1$
.
$\prod _C \mathcal {A}_0 \cong \prod _C \mathcal {A}_1$
.
Proof We first prove the theorem under the assumption that
![]() $\mathfrak {L}$
is a relational language. Let
$\mathfrak {L}$
is a relational language. Let
![]() $\mathcal {A}_0$
and
$\mathcal {A}_0$
and
![]() $\mathcal {A}_1$
be computable
$\mathcal {A}_1$
be computable
![]() $\mathfrak {L}$
-structures, and let
$\mathfrak {L}$
-structures, and let
![]() $f \colon |\mathcal {A}_0| \rightarrow |\mathcal {A}_1|$
be a computable isomorphism. Expand the language to
$f \colon |\mathcal {A}_0| \rightarrow |\mathcal {A}_1|$
be a computable isomorphism. Expand the language to
![]() $\mathfrak {L}^+ = \mathfrak {L} \cup \{U_0, U_1, R_f\}$
, where
$\mathfrak {L}^+ = \mathfrak {L} \cup \{U_0, U_1, R_f\}$
, where
![]() $U_0$
and
$U_0$
and
![]() $U_1$
are fresh unary relation symbols and
$U_1$
are fresh unary relation symbols and
![]() $R_f$
is a fresh binary relation symbol. Expand
$R_f$
is a fresh binary relation symbol. Expand
![]() $\mathcal {A}_0 \sqcup \mathcal {A}_1$
to a computable
$\mathcal {A}_0 \sqcup \mathcal {A}_1$
to a computable
![]() $\mathfrak {L}^+$
-structure by interpreting
$\mathfrak {L}^+$
-structure by interpreting
![]() $U_0$
and
$U_0$
and
![]() $U_1$
as the domains of
$U_1$
as the domains of
![]() $\mathcal {A}_0$
and
$\mathcal {A}_0$
and
![]() $\mathcal {A}_1$
and by interpreting
$\mathcal {A}_1$
and by interpreting
![]() $R_f$
as the graph of f.
$R_f$
as the graph of f.
-
• For each
 $i < 2$
,
$i < 2$
,
 $U_i^{\mathcal {A}_0 \sqcup \mathcal {A}_1}(x)$
holds if and only if
$U_i^{\mathcal {A}_0 \sqcup \mathcal {A}_1}(x)$
holds if and only if
 $\pi _0(x) = i$
.
$\pi _0(x) = i$
. -
•
 $R_f^{\mathcal {A}_0 \sqcup \mathcal {A}_1}(x,y)$
holds if and only if
$R_f^{\mathcal {A}_0 \sqcup \mathcal {A}_1}(x,y)$
holds if and only if
 $\pi _0(x) = 0$
,
$\pi _0(x) = 0$
,
 $\pi _0(y) = 1$
, and
$\pi _0(y) = 1$
, and
 $f(\pi _1(x)) = \pi _1(y)$
.
$f(\pi _1(x)) = \pi _1(y)$
.
The function f is an isomorphism, so
![]() $R_f^{\mathcal {A}_0 \sqcup \mathcal {A}_1}$
is the graph of an isomorphism between
$R_f^{\mathcal {A}_0 \sqcup \mathcal {A}_1}$
is the graph of an isomorphism between
![]() $\mathcal {A}_0$
and
$\mathcal {A}_0$
and
![]() $\mathcal {A}_1$
as
$\mathcal {A}_1$
as
![]() $\mathcal {L}$
-structures in the
$\mathcal {L}$
-structures in the
![]() $\mathfrak {L}^+$
-structure
$\mathfrak {L}^+$
-structure
![]() $\mathcal {A}_0 \sqcup \mathcal {A}_1$
. That is,
$\mathcal {A}_0 \sqcup \mathcal {A}_1$
. That is,
![]() $R_f$
has the following properties in
$R_f$
has the following properties in
![]() $\mathcal {A}_0 \sqcup \mathcal {A}_1$
.
$\mathcal {A}_0 \sqcup \mathcal {A}_1$
.
-
• The domain of
 $R_f$
corresponds to
$R_f$
corresponds to
 $|\mathcal {A}_0|$
:
$|\mathcal {A}_0|$
:
 $\forall x \, (\exists y \, R_f(x, y) \;\leftrightarrow \; U_0(x))$
.
$\forall x \, (\exists y \, R_f(x, y) \;\leftrightarrow \; U_0(x))$
. -
• The image of
 $R_f$
corresponds to
$R_f$
corresponds to
 $|\mathcal {A}_1|$
:
$|\mathcal {A}_1|$
:
 $\forall y \, (\exists x \, R_f(x, y) \;\leftrightarrow \; U_1(y))$
.
$\forall y \, (\exists x \, R_f(x, y) \;\leftrightarrow \; U_1(y))$
. -
•
 $R_f$
is single-valued on its domain:
$R_f$
is single-valued on its domain:
 $\forall x \forall y_0 \forall y_1 \, (R_f(x, y_0) \wedge R_f(x, y_1) \;\rightarrow \; y_0 = y_1)$
.
$\forall x \forall y_0 \forall y_1 \, (R_f(x, y_0) \wedge R_f(x, y_1) \;\rightarrow \; y_0 = y_1)$
. -
•
 $R_f$
is injective on its domain:
$R_f$
is injective on its domain:
 $\forall x_0 \forall x_1 \forall y \, (R_f(x_0, y) \wedge R_f(x_1, y) \;\rightarrow \; x_0 = x_1)$
.
$\forall x_0 \forall x_1 \forall y \, (R_f(x_0, y) \wedge R_f(x_1, y) \;\rightarrow \; x_0 = x_1)$
. -
•
 $R_f$
respects the relations of
$R_f$
respects the relations of
 $\mathfrak {L}$
: for every m-ary relation symbol
$\mathfrak {L}$
: for every m-ary relation symbol
 $S \in \mathfrak {L}$
,
$S \in \mathfrak {L}$
,  $$ \begin{align*} \forall x_0 \ldots \forall x_{m-1} \forall y_0 \ldots \forall y_{m-1} \, \left(\bigwedge_{i < m}R_f(x_i, y_i) \;\rightarrow\; (S(x_0, \dots, x_{m-1}) \leftrightarrow S(y_0, \dots, y_{m-1}))\right). \end{align*} $$
$$ \begin{align*} \forall x_0 \ldots \forall x_{m-1} \forall y_0 \ldots \forall y_{m-1} \, \left(\bigwedge_{i < m}R_f(x_i, y_i) \;\rightarrow\; (S(x_0, \dots, x_{m-1}) \leftrightarrow S(y_0, \dots, y_{m-1}))\right). \end{align*} $$
The above properties constitute a collection of
![]() $\Pi _2\ \mathfrak {L}^+$
-sentences that hold in
$\Pi _2\ \mathfrak {L}^+$
-sentences that hold in
![]() $\mathcal {A}_0 \sqcup \mathcal {A}_1$
, so they also hold in the cohesive power
$\mathcal {A}_0 \sqcup \mathcal {A}_1$
, so they also hold in the cohesive power
![]() $\prod _C(\mathcal {A}_0 \sqcup \mathcal {A}_1)$
as an
$\prod _C(\mathcal {A}_0 \sqcup \mathcal {A}_1)$
as an
![]() $\mathfrak {L}^+$
-structure by Theorem 2.9 item (2). For each
$\mathfrak {L}^+$
-structure by Theorem 2.9 item (2). For each
![]() $i < 2$
, let
$i < 2$
, let
![]() $\mathcal {D}_i$
denote the substructure of
$\mathcal {D}_i$
denote the substructure of
![]() $\prod _C(\mathcal {A}_0 \sqcup \mathcal {A}_1)$
with domain given by
$\prod _C(\mathcal {A}_0 \sqcup \mathcal {A}_1)$
with domain given by
![]() $U_i$
:
$U_i$
:
![]() $|\mathcal {D}_i| = \bigl \{[\varphi ] : \prod _C(\mathcal {A}_0 \sqcup \mathcal {A}_1) \models U_i([\varphi ])\bigr \}$
. Then
$|\mathcal {D}_i| = \bigl \{[\varphi ] : \prod _C(\mathcal {A}_0 \sqcup \mathcal {A}_1) \models U_i([\varphi ])\bigr \}$
. Then
![]() $\prod _C \mathcal {A}_i \cong \mathcal {D}_i {\restriction } \mathfrak {L}$
as an
$\prod _C \mathcal {A}_i \cong \mathcal {D}_i {\restriction } \mathfrak {L}$
as an
![]() $\mathfrak {L}$
-structure for each
$\mathfrak {L}$
-structure for each
![]() $i < 2$
by Proposition 2.12. In
$i < 2$
by Proposition 2.12. In
![]() $\prod _C(\mathcal {A}_0 \sqcup \mathcal {A}_1)$
,
$\prod _C(\mathcal {A}_0 \sqcup \mathcal {A}_1)$
,
![]() $R_f^{\prod _C(\mathcal {A}_0 \sqcup \mathcal {A}_1)}$
is the graph of an isomorphism between the reducts
$R_f^{\prod _C(\mathcal {A}_0 \sqcup \mathcal {A}_1)}$
is the graph of an isomorphism between the reducts
![]() $\mathcal {D}_0 {\restriction } \mathfrak {L}$
and
$\mathcal {D}_0 {\restriction } \mathfrak {L}$
and
![]() $\mathcal {D}_1 {\restriction } \mathfrak {L}$
. Therefore
$\mathcal {D}_1 {\restriction } \mathfrak {L}$
. Therefore
![]() $\prod _C \mathcal {A}_0 \cong \prod _C \mathcal {A}_1$
as
$\prod _C \mathcal {A}_0 \cong \prod _C \mathcal {A}_1$
as
![]() $\mathfrak {L}$
-structures.
$\mathfrak {L}$
-structures.
Now suppose that
![]() $\mathfrak {L}$
contains constant and function symbols in addition to relation symbols. For uniformity of argument, treat constant symbols as
$\mathfrak {L}$
contains constant and function symbols in addition to relation symbols. For uniformity of argument, treat constant symbols as
![]() $0$
-ary function symbols. Let
$0$
-ary function symbols. Let
![]() $\mathfrak {L}^{\mathsf {rel}}$
be the relational language obtained from
$\mathfrak {L}^{\mathsf {rel}}$
be the relational language obtained from
![]() $\mathfrak {L}$
by replacing each m-ary function symbol f by a fresh
$\mathfrak {L}$
by replacing each m-ary function symbol f by a fresh
![]() $(m+1)$
-ary relation symbol
$(m+1)$
-ary relation symbol
![]() $G_f$
whose intended interpretation is the graph of f. We may translate any
$G_f$
whose intended interpretation is the graph of f. We may translate any
![]() $\mathfrak {L}$
-structure
$\mathfrak {L}$
-structure
![]() $\mathcal {A}$
into an
$\mathcal {A}$
into an
![]() $\mathfrak {L}^{\mathsf {rel}}$
-structure
$\mathfrak {L}^{\mathsf {rel}}$
-structure
![]() $\mathcal {A}^{\mathsf {rel}}$
with the same domain by defining
$\mathcal {A}^{\mathsf {rel}}$
with the same domain by defining
for every m-ary function symbol
![]() $f \in \mathfrak {L}$
and every
$f \in \mathfrak {L}$
and every
![]() $x_0, \dots , x_{m-1}, y \in |\mathcal {A}|$
. Conversely, suppose that
$x_0, \dots , x_{m-1}, y \in |\mathcal {A}|$
. Conversely, suppose that
![]() $\mathcal {A}$
is an
$\mathcal {A}$
is an
![]() $\mathfrak {L}^{\mathsf {rel}}$
-structure such that for every m-ary function symbol
$\mathfrak {L}^{\mathsf {rel}}$
-structure such that for every m-ary function symbol
![]() $f \in \mathfrak {L}$
,
$f \in \mathfrak {L}$
,
![]() $G_f$
is the graph of a function:
$G_f$
is the graph of a function:
![]() $\forall x_0 \ldots \forall x_{m-1} \exists ! {y} \, G_f^{\mathcal {A}}(x_0, \dots , x_{m-1}, y)$
. Then we may translate
$\forall x_0 \ldots \forall x_{m-1} \exists ! {y} \, G_f^{\mathcal {A}}(x_0, \dots , x_{m-1}, y)$
. Then we may translate
![]() $\mathcal {A}$
into an
$\mathcal {A}$
into an
![]() $\mathfrak {L}$
-structure
$\mathfrak {L}$
-structure
![]() $\mathcal {A}^{\mathsf {fun}}$
with the same domain by defining
$\mathcal {A}^{\mathsf {fun}}$
with the same domain by defining
![]() $f^{\mathcal {A}^{\mathsf {fun}}}(x_0, \dots , x_{m-1})$
to be the unique y such that
$f^{\mathcal {A}^{\mathsf {fun}}}(x_0, \dots , x_{m-1})$
to be the unique y such that
![]() $G_f^{\mathcal {A}}(x_0, \dots , x_{m-1}, y)$
for every m-ary function symbol
$G_f^{\mathcal {A}}(x_0, \dots , x_{m-1}, y)$
for every m-ary function symbol
![]() $f \in \mathfrak {L}$
and every
$f \in \mathfrak {L}$
and every
![]() $x_0, \dots , x_{m-1} \in |\mathcal {A}|$
. If
$x_0, \dots , x_{m-1} \in |\mathcal {A}|$
. If
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are isomorphic
$\mathcal {B}$
are isomorphic
![]() $\mathfrak {L}$
-structures, then the isomorphism is also an isomorphism between
$\mathfrak {L}$
-structures, then the isomorphism is also an isomorphism between
![]() $\mathcal {A}^{\mathsf {rel}}$
and
$\mathcal {A}^{\mathsf {rel}}$
and
![]() $\mathcal {B}^{\mathsf {rel}}$
as
$\mathcal {B}^{\mathsf {rel}}$
as
![]() $\mathfrak {L}^{\mathsf {rel}}$
-structures. Conversely, if
$\mathfrak {L}^{\mathsf {rel}}$
-structures. Conversely, if
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are isomorphic
$\mathcal {B}$
are isomorphic
![]() $\mathfrak {L}^{\mathsf {rel}}$
-structures such that
$\mathfrak {L}^{\mathsf {rel}}$
-structures such that
![]() $G_f$
is the graph of a function in both structures for every function symbol
$G_f$
is the graph of a function in both structures for every function symbol
![]() $f \in \mathfrak {L}$
, then the isomorphism is also an isomorphism between
$f \in \mathfrak {L}$
, then the isomorphism is also an isomorphism between
![]() $\mathcal {A}^{\mathsf {fun}}$
and
$\mathcal {A}^{\mathsf {fun}}$
and
![]() $\mathcal {B}^{\mathsf {fun}}$
as
$\mathcal {B}^{\mathsf {fun}}$
as
![]() $\mathfrak {L}$
-structures.
$\mathfrak {L}$
-structures.
If
![]() $\mathfrak {L}$
is a computable language and
$\mathfrak {L}$
is a computable language and
![]() $\mathcal {A}$
is a computable
$\mathcal {A}$
is a computable
![]() $\mathfrak {L}$
-structure, then
$\mathfrak {L}$
-structure, then
![]() $\mathfrak {L}^{\mathsf {rel}}$
is a computable language and
$\mathfrak {L}^{\mathsf {rel}}$
is a computable language and
![]() $\mathcal {A}^{\mathsf {rel}}$
is a computable
$\mathcal {A}^{\mathsf {rel}}$
is a computable
![]() $\mathfrak {L}^{\mathsf {rel}}$
-structure. Let
$\mathfrak {L}^{\mathsf {rel}}$
-structure. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be computably isomorphic
$\mathcal {B}$
be computably isomorphic
![]() $\mathfrak {L}$
-structures, and let C be a cohesive set. Then
$\mathfrak {L}$
-structures, and let C be a cohesive set. Then
![]() $\mathcal {A}^{\mathsf {rel}}$
and
$\mathcal {A}^{\mathsf {rel}}$
and
![]() $\mathcal {B}^{\mathsf {rel}}$
are computably isomorphic computable
$\mathcal {B}^{\mathsf {rel}}$
are computably isomorphic computable
![]() $\mathcal {L}^{\mathsf {rel}}$
-structures, so
$\mathcal {L}^{\mathsf {rel}}$
-structures, so
![]() $\prod _C \mathcal {A}^{\mathsf {rel}} \cong \prod _C \mathcal {B}^{\mathsf {rel}}$
as
$\prod _C \mathcal {A}^{\mathsf {rel}} \cong \prod _C \mathcal {B}^{\mathsf {rel}}$
as
![]() $\mathfrak {L}^{\mathsf {rel}}$
-structures. For each function symbol
$\mathfrak {L}^{\mathsf {rel}}$
-structures. For each function symbol
![]() $f \in \mathfrak {L}$
,
$f \in \mathfrak {L}$
,
![]() $G_f$
is the graph of a function in
$G_f$
is the graph of a function in
![]() $\mathcal {A}^{\mathsf {rel}}$
and in
$\mathcal {A}^{\mathsf {rel}}$
and in
![]() $\mathcal {B}^{\mathsf {rel}}$
. Therefore
$\mathcal {B}^{\mathsf {rel}}$
. Therefore
![]() $G_f$
is the graph of a function in
$G_f$
is the graph of a function in
![]() $\prod _C \mathcal {A}^{\mathsf {rel}}$
and in
$\prod _C \mathcal {A}^{\mathsf {rel}}$
and in
![]() $\prod _C \mathcal {B}^{\mathsf {rel}}$
by Theorem 2.9 item (2) because the statement “
$\prod _C \mathcal {B}^{\mathsf {rel}}$
by Theorem 2.9 item (2) because the statement “
![]() $G_f$
is the graph of a function” is expressible by a
$G_f$
is the graph of a function” is expressible by a
![]() $\Pi _2\ \mathfrak {L}^{\mathsf {rel}}$
-sentence. Therefore
$\Pi _2\ \mathfrak {L}^{\mathsf {rel}}$
-sentence. Therefore
![]() $(\prod _C \mathcal {A}^{\mathsf {rel}})^{\mathsf {fun}} \,\cong \, (\prod _C \mathcal {B}^{\mathsf {rel}})^{\mathsf {fun}}$
as
$(\prod _C \mathcal {A}^{\mathsf {rel}})^{\mathsf {fun}} \,\cong \, (\prod _C \mathcal {B}^{\mathsf {rel}})^{\mathsf {fun}}$
as
![]() $\mathfrak {L}$
-structures. It is straightforward to check that
$\mathfrak {L}$
-structures. It is straightforward to check that
![]() $\prod _C \mathcal {A}^{\mathsf {rel}} = (\prod _C \mathcal {A})^{\mathsf {rel}}$
and therefore that
$\prod _C \mathcal {A}^{\mathsf {rel}} = (\prod _C \mathcal {A})^{\mathsf {rel}}$
and therefore that
![]() $(\prod _C \mathcal {A}^{\mathsf {rel}})^{\mathsf {fun}} = \prod _C \mathcal {A}$
; and similarly for
$(\prod _C \mathcal {A}^{\mathsf {rel}})^{\mathsf {fun}} = \prod _C \mathcal {A}$
; and similarly for
![]() $\mathcal {B}$
. Thus
$\mathcal {B}$
. Thus
![]() $\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
as
$\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
as
![]() $\mathfrak {L}$
-structures, as desired.
$\mathfrak {L}$
-structures, as desired.
Recall that a computable structure
![]() $\mathcal {A}$
is called computably categorical if every computable structure that is isomorphic to
$\mathcal {A}$
is called computably categorical if every computable structure that is isomorphic to
![]() $\mathcal {A}$
is isomorphic to
$\mathcal {A}$
is isomorphic to
![]() $\mathcal {A}$
via a computable isomorphism. It follows from Theorem 2.20 that if
$\mathcal {A}$
via a computable isomorphism. It follows from Theorem 2.20 that if
![]() $\mathcal {A}$
is a computably categorical computable structure and C is cohesive, then
$\mathcal {A}$
is a computably categorical computable structure and C is cohesive, then
![]() $\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
whenever
$\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
whenever
![]() $\mathcal {B}$
is a computable structure isomorphic to
$\mathcal {B}$
is a computable structure isomorphic to
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Corollary 2.21. Let
![]() $\mathfrak {L}$
be a computable language, let
$\mathfrak {L}$
be a computable language, let
![]() $\mathcal {A}$
be a computably categorical computable
$\mathcal {A}$
be a computably categorical computable
![]() $\mathfrak {L}$
-structure, let
$\mathfrak {L}$
-structure, let
![]() $\mathcal {B}$
be a computable
$\mathcal {B}$
be a computable
![]() $\mathfrak {L}$
-structure that is isomorphic to
$\mathfrak {L}$
-structure that is isomorphic to
![]() $\mathcal {A}$
, and let C be cohesive. Then
$\mathcal {A}$
, and let C be cohesive. Then
![]() $\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
.
$\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
.
In Theorem 2.20, it is essential that the two structures are isomorphic via a computable isomorphism. In Sections 4–6, we see many examples of pairs of computable linear orders that are isomorphic (but not computably isomorphic) to
![]() $\omega $
but have non-elementarily equivalent cohesive powers.
$\omega $
but have non-elementarily equivalent cohesive powers.
The next theorem says that decidable structures
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
are elementarily equivalent if and only if
$\mathcal {B}$
are elementarily equivalent if and only if
![]() $\prod _C \mathcal {A}$
and
$\prod _C \mathcal {A}$
and
![]() $\prod _C \mathcal {B}$
are isomorphic for every cohesive set C. It is essentially [Reference Nelson20, Theorem 2.1], though we give a slightly different proof. Compare this to the Keisler–Shelah theorem, which states that, in general, two structures are elementarily equivalent if and only if there is an ultrafilter (on a set of appropriate size) over which the corresponding ultrapowers are isomorphic (see [Reference Chang and Keisler2, Theorem 6.1.15]).
$\prod _C \mathcal {B}$
are isomorphic for every cohesive set C. It is essentially [Reference Nelson20, Theorem 2.1], though we give a slightly different proof. Compare this to the Keisler–Shelah theorem, which states that, in general, two structures are elementarily equivalent if and only if there is an ultrafilter (on a set of appropriate size) over which the corresponding ultrapowers are isomorphic (see [Reference Chang and Keisler2, Theorem 6.1.15]).
Theorem 2.22. Let
![]() $\mathfrak {L}$
be a computable language, and let
$\mathfrak {L}$
be a computable language, and let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be decidable
$\mathcal {B}$
be decidable
![]() $\mathfrak {L}$
-structures. Then
$\mathfrak {L}$
-structures. Then
![]() $\mathcal {A} \equiv \mathcal {B}$
if and only if for every cohesive set C,
$\mathcal {A} \equiv \mathcal {B}$
if and only if for every cohesive set C,
![]() $\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
.
$\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
.
Proof In general, say that two structures
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
have the same types (without parameters) if for every sequence
$\mathcal {N}$
have the same types (without parameters) if for every sequence
![]() $\vec {a} = a_0, \dots , a_{m-1}$
of elements of
$\vec {a} = a_0, \dots , a_{m-1}$
of elements of
![]() $|\mathcal {M}|$
, there is a corresponding sequence
$|\mathcal {M}|$
, there is a corresponding sequence
![]() $\vec {b} = b_0, \dots , b_{m-1}$
of elements of
$\vec {b} = b_0, \dots , b_{m-1}$
of elements of
![]() $|\mathcal {N}|$
such that for every formula
$|\mathcal {N}|$
such that for every formula
![]() $\Phi (x_0, \dots , x_{m-1})$
with m free variables,
$\Phi (x_0, \dots , x_{m-1})$
with m free variables,
and similarly with the roles of
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
reversed. Now recall [Reference Kaye15, Corollary 15.15], which states that if
$\mathcal {N}$
reversed. Now recall [Reference Kaye15, Corollary 15.15], which states that if
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
are countable recursively saturated
$\mathcal {N}$
are countable recursively saturated
![]() $\mathfrak {L}$
-structures, then
$\mathfrak {L}$
-structures, then
![]() $\mathcal {M} \cong \mathcal {N}$
if and only if
$\mathcal {M} \cong \mathcal {N}$
if and only if
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {N}$
are elementarily equivalent and have the same types.
$\mathcal {N}$
are elementarily equivalent and have the same types.
For the forward direction, let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be decidable
$\mathcal {B}$
be decidable
![]() $\mathfrak {L}$
-structures that are elementarily equivalent, and let C be cohesive. Then
$\mathfrak {L}$
-structures that are elementarily equivalent, and let C be cohesive. Then
![]() $\prod _C \mathcal {A}$
and
$\prod _C \mathcal {A}$
and
![]() $\prod _C \mathcal {B}$
are countable, are elementarily equivalent by Corollary 2.10 (which yields that
$\prod _C \mathcal {B}$
are countable, are elementarily equivalent by Corollary 2.10 (which yields that
![]() $\prod _C \mathcal {A} \equiv \mathcal {A} \equiv \mathcal {B} \equiv \prod _C \mathcal {B}$
), and are recursively saturated by Theorem 2.16. Thus to conclude that
$\prod _C \mathcal {A} \equiv \mathcal {A} \equiv \mathcal {B} \equiv \prod _C \mathcal {B}$
), and are recursively saturated by Theorem 2.16. Thus to conclude that
![]() $\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
, it suffices to show that
$\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
, it suffices to show that
![]() $\prod _C \mathcal {A}$
and
$\prod _C \mathcal {A}$
and
![]() $\prod _C \mathcal {B}$
have the same types.
$\prod _C \mathcal {B}$
have the same types.
We show that for every
![]() $[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}|$
, there are
$[\varphi _0], \dots , [\varphi _{m-1}] \in |\prod _C \mathcal {A}|$
, there are
![]() $[\psi _0], \dots , [\psi _{m-1}] \in |\prod _C \mathcal {B}|$
with the same type. A symmetric argument shows that the same holds with the roles of
$[\psi _0], \dots , [\psi _{m-1}] \in |\prod _C \mathcal {B}|$
with the same type. A symmetric argument shows that the same holds with the roles of
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
reversed. As in the proofs of Lemmas 2.15 and 2.17, let
$\mathcal {B}$
reversed. As in the proofs of Lemmas 2.15 and 2.17, let
![]() $\varphi \colon \mathbb {N} \rightarrow \mathbb {N}^m$
be the partial computable function
$\varphi \colon \mathbb {N} \rightarrow \mathbb {N}^m$
be the partial computable function
![]() $\varphi (n) \simeq \langle \varphi _0(n), \dots , \varphi _{m-1}(n) \rangle $
, and let
$\varphi (n) \simeq \langle \varphi _0(n), \dots , \varphi _{m-1}(n) \rangle $
, and let
![]() $\overrightarrow {[\varphi ]}$
denote
$\overrightarrow {[\varphi ]}$
denote
![]() $[\varphi _0], \dots , [\varphi _{m-1}]$
. Note that
$[\varphi _0], \dots , [\varphi _{m-1}]$
. Note that
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
. Let
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
. Let
![]() $(\Phi _i(\vec {x}) : i \in \mathbb {N})$
be a computable enumeration of all formulas with m free variables.
$(\Phi _i(\vec {x}) : i \in \mathbb {N})$
be a computable enumeration of all formulas with m free variables.
Define a partial computable function
![]() $\psi \colon \mathbb {N} \rightarrow \mathbb {N}^m$
as follows. If
$\psi \colon \mathbb {N} \rightarrow \mathbb {N}^m$
as follows. If
![]() $\varphi (n){\downarrow }$
, then for each
$\varphi (n){\downarrow }$
, then for each
![]() $i \leq n$
, use the decidability of
$i \leq n$
, use the decidability of
![]() $\mathcal {A}$
to determine whether
$\mathcal {A}$
to determine whether
![]() $\mathcal {A} \models \Phi _i(\varphi (n))$
. If
$\mathcal {A} \models \Phi _i(\varphi (n))$
. If
![]() $\mathcal {A} \models \Phi _i(\varphi (n))$
, let
$\mathcal {A} \models \Phi _i(\varphi (n))$
, let
![]() $\Theta _i = \Phi _i$
; and if
$\Theta _i = \Phi _i$
; and if
![]() $\mathcal {A} \not \models \Phi _i(\varphi (n))$
, let
$\mathcal {A} \not \models \Phi _i(\varphi (n))$
, let
![]() $\Theta _i = \neg \Phi _i$
. Then
$\Theta _i = \neg \Phi _i$
. Then
![]() $\varphi (n)$
witnesses that
$\varphi (n)$
witnesses that
![]() $\mathcal {A} \models \exists \vec {x}\, \bigwedge _{i \leq n} \Theta _i (\vec {x})$
, so
$\mathcal {A} \models \exists \vec {x}\, \bigwedge _{i \leq n} \Theta _i (\vec {x})$
, so
![]() $\mathcal {B} \models \exists \vec {x}\, \bigwedge _{i \leq n} \Theta _i (\vec {x})$
because
$\mathcal {B} \models \exists \vec {x}\, \bigwedge _{i \leq n} \Theta _i (\vec {x})$
because
![]() $\mathcal {B} \equiv \mathcal {A}$
. By the decidability of
$\mathcal {B} \equiv \mathcal {A}$
. By the decidability of
![]() $\mathcal {B}$
, search for the first
$\mathcal {B}$
, search for the first
![]() $\vec {b}$
such that
$\vec {b}$
such that
![]() $\mathcal {B} \models \bigwedge _{i \leq n} \Theta _i (\vec {b})$
, and define
$\mathcal {B} \models \bigwedge _{i \leq n} \Theta _i (\vec {b})$
, and define
![]() $\psi (n) = \vec {b}$
. On the other hand, if
$\psi (n) = \vec {b}$
. On the other hand, if
![]() $\varphi (n){\uparrow }$
, then
$\varphi (n){\uparrow }$
, then
![]() $\psi (n){\uparrow }$
.
$\psi (n){\uparrow }$
.
Consider the formula
![]() $\Phi _i$
, and suppose that
$\Phi _i$
, and suppose that
![]() $\prod _C \mathcal {A} \models \Phi _i \left (\overrightarrow {[\varphi ]}\right )$
. Then
$\prod _C \mathcal {A} \models \Phi _i \left (\overrightarrow {[\varphi ]}\right )$
. Then
![]() $C \subseteq ^* \{n : \mathcal {A} \models \Phi _i(\varphi (n))\}$
by Corollary 2.10. Thus for sufficiently large
$C \subseteq ^* \{n : \mathcal {A} \models \Phi _i(\varphi (n))\}$
by Corollary 2.10. Thus for sufficiently large
![]() $n \geq i$
with
$n \geq i$
with
![]() $n \in C$
, we have that
$n \in C$
, we have that
![]() $\Theta _i = \Phi _i$
in the computation of
$\Theta _i = \Phi _i$
in the computation of
![]() $\psi (n)$
, and therefore
$\psi (n)$
, and therefore
![]() $\psi (n)$
is defined so that
$\psi (n)$
is defined so that
![]() $\mathcal {B} \models \Phi _i(\psi (n))$
. Thus
$\mathcal {B} \models \Phi _i(\psi (n))$
. Thus
![]() $C \subseteq ^* \{n : \mathcal {B} \models \Phi _i(\psi (n))\}$
. Letting
$C \subseteq ^* \{n : \mathcal {B} \models \Phi _i(\psi (n))\}$
. Letting
![]() $\psi _j = \pi _j \circ \psi $
for each
$\psi _j = \pi _j \circ \psi $
for each
![]() $j < m$
yields that
$j < m$
yields that
![]() $\prod _C \mathcal {B} \models \Phi _i \left (\overrightarrow {[\psi ]}\right )$
by Corollary 2.10. If instead
$\prod _C \mathcal {B} \models \Phi _i \left (\overrightarrow {[\psi ]}\right )$
by Corollary 2.10. If instead
![]() $\prod _C \mathcal {A} \models \neg \Phi _i \left (\overrightarrow {[\varphi ]}\right )$
, then
$\prod _C \mathcal {A} \models \neg \Phi _i \left (\overrightarrow {[\varphi ]}\right )$
, then
![]() $\prod _C \mathcal {B} \models \neg \Phi _i \left (\overrightarrow {[\psi ]}\right )$
by a similar argument. Thus
$\prod _C \mathcal {B} \models \neg \Phi _i \left (\overrightarrow {[\psi ]}\right )$
by a similar argument. Thus
![]() $[\psi _0], \dots , [\psi _{m-1}]$
has in
$[\psi _0], \dots , [\psi _{m-1}]$
has in
![]() $\prod _C \mathcal {B}$
the same type that
$\prod _C \mathcal {B}$
the same type that
![]() $[\varphi _0], \dots , [\varphi _{m-1}]$
has in
$[\varphi _0], \dots , [\varphi _{m-1}]$
has in
![]() $\prod _C \mathcal {A}$
, as desired.
$\prod _C \mathcal {A}$
, as desired.
For the converse, let
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {B}$
be decidable
$\mathcal {B}$
be decidable
![]() $\mathfrak {L}$
-structures, and suppose that
$\mathfrak {L}$
-structures, and suppose that
![]() $\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
for every cohesive set C. Fix any cohesive set C. Then
$\prod _C \mathcal {A} \cong \prod _C \mathcal {B}$
for every cohesive set C. Fix any cohesive set C. Then
![]() $\mathcal {A} \equiv \prod _C \mathcal {A} \equiv \prod _C \mathcal {B} \equiv \mathcal {B}$
by Corollary 2.10.
$\mathcal {A} \equiv \prod _C \mathcal {A} \equiv \prod _C \mathcal {B} \equiv \mathcal {B}$
by Corollary 2.10.
Again, the decidability assumption in Theorem 2.22 is essential, as we shall see examples of isomorphic (and hence elementarily equivalent) computable linear orders having non-elementarily equivalent (and hence non-isomorphic) cohesive powers. We shall also see examples of non-elementarily equivalent computable linear orders having isomorphic cohesive powers.
3 Linear orders and their cohesive powers
We investigate the cohesive powers of computable linear orders, with special attention to computable linear orders of type
![]() $\omega $
. A linear order
$\omega $
. A linear order
![]() $\mathcal {L} = (L, \prec )$
consists of a non-empty set L equipped with a binary relation
$\mathcal {L} = (L, \prec )$
consists of a non-empty set L equipped with a binary relation
![]() $\prec $
satisfying the following axioms:
$\prec $
satisfying the following axioms:
-
•
 $\forall x \, (x \nprec x)$
.
$\forall x \, (x \nprec x)$
. -
•
 $\forall x \forall y \forall z \, [(x \prec y \wedge y \prec z) \;\rightarrow \; x \prec z]$
.
$\forall x \forall y \forall z \, [(x \prec y \wedge y \prec z) \;\rightarrow \; x \prec z]$
. -
•
 $\forall x \forall y \, (x \prec y \,\vee \, x = y \,\vee \, y \prec x)$
.
$\forall x \forall y \, (x \prec y \,\vee \, x = y \,\vee \, y \prec x)$
.
Additionally, a linear order
![]() $\mathcal {L}$
is dense if
$\mathcal {L}$
is dense if
![]() $\forall x \forall y \exists z \, (x \prec y \,\rightarrow \, x \prec z \prec y)$
and has no endpoints if
$\forall x \forall y \exists z \, (x \prec y \,\rightarrow \, x \prec z \prec y)$
and has no endpoints if
![]() $\forall x \exists y \exists z \, (y \prec x \prec z)$
. Rosenstein’s book [Reference Rosenstein21] is an excellent reference for linear orders.
$\forall x \exists y \exists z \, (y \prec x \prec z)$
. Rosenstein’s book [Reference Rosenstein21] is an excellent reference for linear orders.
For a linear order
![]() $\mathcal {L} = (L, \prec )$
, we use the usual interval notation
$\mathcal {L} = (L, \prec )$
, we use the usual interval notation
![]() $(a,b)_{\mathcal {L}} = \{x \in L : a \prec x \prec b\}$
and
$(a,b)_{\mathcal {L}} = \{x \in L : a \prec x \prec b\}$
and
![]() $[a,b]_{\mathcal {L}} = \{x \in L : a \preceq x \preceq b\}$
to denote open and closed intervals of
$[a,b]_{\mathcal {L}} = \{x \in L : a \preceq x \preceq b\}$
to denote open and closed intervals of
![]() $\mathcal {L}$
. Sometimes it is convenient to allow
$\mathcal {L}$
. Sometimes it is convenient to allow
![]() $b \preceq a$
in this notation, in which case, for example,
$b \preceq a$
in this notation, in which case, for example,
![]() $(a,b)_{\mathcal {L}} = \emptyset $
. The notation
$(a,b)_{\mathcal {L}} = \emptyset $
. The notation
![]() $|(a,b)_{\mathcal {L}}|$
denotes the cardinality of the interval
$|(a,b)_{\mathcal {L}}|$
denotes the cardinality of the interval
![]() $(a,b)_{\mathcal {L}}$
. The notations
$(a,b)_{\mathcal {L}}$
. The notations
![]() $\min _\prec \{a, b\}$
and
$\min _\prec \{a, b\}$
and
![]() $\max _\prec \{a, b\}$
denote the minimum and maximum of a and b with respect to
$\max _\prec \{a, b\}$
denote the minimum and maximum of a and b with respect to
![]() $\prec $
.
$\prec $
.
As is customary,
![]() $\omega $
denotes the order-type of
$\omega $
denotes the order-type of
![]() $(\mathbb {N}, <)$
,
$(\mathbb {N}, <)$
,
![]() $\zeta $
denotes the order-type of
$\zeta $
denotes the order-type of
![]() $(\mathbb {Z}, <)$
, and
$(\mathbb {Z}, <)$
, and
![]() $\eta $
denotes the order-type of
$\eta $
denotes the order-type of
![]() $(\mathbb {Q}, <)$
. That is,
$(\mathbb {Q}, <)$
. That is,
![]() $\omega $
,
$\omega $
,
![]() $\zeta $
, and
$\zeta $
, and
![]() $\eta $
denote the respective order-types of the natural numbers, the integers, and the rationals, each with their usual order. We refer to
$\eta $
denote the respective order-types of the natural numbers, the integers, and the rationals, each with their usual order. We refer to
![]() $(\mathbb {N}, <)$
,
$(\mathbb {N}, <)$
,
![]() $(\mathbb {Z}, <)$
, and
$(\mathbb {Z}, <)$
, and
![]() $(\mathbb {Q}, <)$
as the usual presentations of
$(\mathbb {Q}, <)$
as the usual presentations of
![]() $\omega $
,
$\omega $
,
![]() $\zeta $
, and
$\zeta $
, and
![]() $\eta $
, respectively. Recall that every countable dense linear order without endpoints has order-type
$\eta $
, respectively. Recall that every countable dense linear order without endpoints has order-type
![]() $\eta $
(see [Reference Rosenstein21, Theorem 2.8]). Furthermore, every computable countable dense linear order without endpoints is computably isomorphic to
$\eta $
(see [Reference Rosenstein21, Theorem 2.8]). Furthermore, every computable countable dense linear order without endpoints is computably isomorphic to
![]() $(\mathbb {Q}, <)$
(see [Reference Rosenstein21, Exercise 16.4]).
$(\mathbb {Q}, <)$
(see [Reference Rosenstein21, Exercise 16.4]).
To help reason about order-types, we use the sum, product, and reverse of linear orders as well as condensations of linear orders.
Definition 3.1. Let
![]() $\mathcal {L}_0 = (L_0, \prec _{\mathcal {L}_0})$
and
$\mathcal {L}_0 = (L_0, \prec _{\mathcal {L}_0})$
and
![]() $\mathcal {L}_1 = (L_0, \prec _{\mathcal {L}_1})$
be linear orders.
$\mathcal {L}_1 = (L_0, \prec _{\mathcal {L}_1})$
be linear orders.
-
• The sum
 $\mathcal {L}_0 + \mathcal {L}_1$
of
$\mathcal {L}_0 + \mathcal {L}_1$
of
 $\mathcal {L}_0$
and
$\mathcal {L}_0$
and
 $\mathcal {L}_1$
is the linear order
$\mathcal {L}_1$
is the linear order
 $\mathcal {S} = (S, \prec _{\mathcal {S}})$
, where
$\mathcal {S} = (S, \prec _{\mathcal {S}})$
, where
 $S = (\{0\} \times L_0) \cup (\{1\} \times L_1)$
and
$S = (\{0\} \times L_0) \cup (\{1\} \times L_1)$
and  $$ \begin{align*} (i, x) \prec_{\mathcal{S}} (j, y) \quad\text{if and only if}\quad (i < j) \;\vee\; (i = j \,\wedge\, x \prec_{\mathcal{L}_i} y). \end{align*} $$
$$ \begin{align*} (i, x) \prec_{\mathcal{S}} (j, y) \quad\text{if and only if}\quad (i < j) \;\vee\; (i = j \,\wedge\, x \prec_{\mathcal{L}_i} y). \end{align*} $$
-
• The product
 $\mathcal {L}_0 \mathcal {L}_1$
of
$\mathcal {L}_0 \mathcal {L}_1$
of
 $\mathcal {L}_0$
and
$\mathcal {L}_0$
and
 $\mathcal {L}_1$
is the linear order
$\mathcal {L}_1$
is the linear order
 $\mathcal {P} = (P, \prec _{\mathcal {P}})$
, where
$\mathcal {P} = (P, \prec _{\mathcal {P}})$
, where
 $P = L_1 \times L_0$
and Note that, by (fairly entrenched) convention,
$P = L_1 \times L_0$
and Note that, by (fairly entrenched) convention, $$ \begin{align*} (x, a) \prec_{\mathcal{P}} (y, b) \quad\text{if and only if}\quad (x \prec_{\mathcal{L}_1} y) \;\vee\; (x = y \,\wedge\, a \prec_{\mathcal{L}_0} b). \end{align*} $$
$$ \begin{align*} (x, a) \prec_{\mathcal{P}} (y, b) \quad\text{if and only if}\quad (x \prec_{\mathcal{L}_1} y) \;\vee\; (x = y \,\wedge\, a \prec_{\mathcal{L}_0} b). \end{align*} $$
 $\mathcal {L}_0 \mathcal {L}_1$
is given by the product order on
$\mathcal {L}_0 \mathcal {L}_1$
is given by the product order on
 $L_1 \times L_0$
, not on
$L_1 \times L_0$
, not on
 $L_0 \times L_1$
.
$L_0 \times L_1$
.
-
• The reverse
 $\mathcal {L}_0^*$
of
$\mathcal {L}_0^*$
of
 $\mathcal {L}_0$
is the linear order
$\mathcal {L}_0$
is the linear order
 $\mathcal {R} = (R, \prec _{\mathcal {R}})$
, where
$\mathcal {R} = (R, \prec _{\mathcal {R}})$
, where
 $R = L_0$
and
$R = L_0$
and
 $x \prec _{\mathcal {R}} y$
if and only if
$x \prec _{\mathcal {R}} y$
if and only if
 $y \prec _{\mathcal {L}_0} x$
. (We warn the reader that the
$y \prec _{\mathcal {L}_0} x$
. (We warn the reader that the
 $*$
in the notation
$*$
in the notation
 $\mathcal {L}_0^*$
is unrelated to the
$\mathcal {L}_0^*$
is unrelated to the
 $*$
in the notation
$*$
in the notation
 $X \subseteq ^* Y$
.)
$X \subseteq ^* Y$
.)
If
![]() $\mathcal {L}_0$
and
$\mathcal {L}_0$
and
![]() $\mathcal {L}_1$
are computable linear orders, then one may use the pairing function to compute copies of
$\mathcal {L}_1$
are computable linear orders, then one may use the pairing function to compute copies of
![]() $\mathcal {L}_0 + \mathcal {L}_1$
and
$\mathcal {L}_0 + \mathcal {L}_1$
and
![]() $\mathcal {L}_0 \mathcal {L}_1$
. Clearly, if
$\mathcal {L}_0 \mathcal {L}_1$
. Clearly, if
![]() $\mathcal {L}$
is a computable linear order, then so is
$\mathcal {L}$
is a computable linear order, then so is
![]() $\mathcal {L}^*$
.
$\mathcal {L}^*$
.
Definition 3.2. Let
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
be a linear order. A condensation of
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
be a linear order. A condensation of
![]() $\mathcal {L}$
is any linear order
$\mathcal {L}$
is any linear order
![]() $\mathcal {M} = (M, \prec _{\mathcal {M}})$
obtained by partitioning L into a collection M of non-empty intervals and, for intervals
$\mathcal {M} = (M, \prec _{\mathcal {M}})$
obtained by partitioning L into a collection M of non-empty intervals and, for intervals
![]() $I, J \in M$
, defining
$I, J \in M$
, defining
![]() $I \prec _{\mathcal {M}} J$
if and only if
$I \prec _{\mathcal {M}} J$
if and only if
![]() $(\forall a \in I)(\forall b \in J)(a \prec _{\mathcal {L}} b)$
.
$(\forall a \in I)(\forall b \in J)(a \prec _{\mathcal {L}} b)$
.
The most important condensation is the finite condensation.
Definition 3.3. Let
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
be a linear order. For
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
be a linear order. For
![]() $x \in L$
, let
$x \in L$
, let
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(x)$
denote the set of
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(x)$
denote the set of
![]() $y \in L$
for which there are only finitely many elements between x and y:
$y \in L$
for which there are only finitely many elements between x and y:
The set
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(x)$
is always a non-empty interval because
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(x)$
is always a non-empty interval because
![]() $x \in \operatorname {{\mathbf {c}_{\mathrm {F}}}}(x)$
. The finite condensation
$x \in \operatorname {{\mathbf {c}_{\mathrm {F}}}}(x)$
. The finite condensation
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\mathcal {L})$
of
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\mathcal {L})$
of
![]() $\mathcal {L}$
is the condensation obtained from the partition
$\mathcal {L}$
is the condensation obtained from the partition
![]() $\{\operatorname {{\mathbf {c}_{\mathrm {F}}}}(x) : x \in L\}$
.
$\{\operatorname {{\mathbf {c}_{\mathrm {F}}}}(x) : x \in L\}$
.
For example,
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\omega ) \cong \boldsymbol {1}$
,
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\omega ) \cong \boldsymbol {1}$
,
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\zeta ) \cong \boldsymbol {1}$
,
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\zeta ) \cong \boldsymbol {1}$
,
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\eta ) \cong \eta $
, and
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\eta ) \cong \eta $
, and
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\omega + \zeta \eta ) \cong \boldsymbol {1} + \eta $
. Notice that for an element x of a linear order
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\omega + \zeta \eta ) \cong \boldsymbol {1} + \eta $
. Notice that for an element x of a linear order
![]() $\mathcal {L}$
, the order-type of
$\mathcal {L}$
, the order-type of
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(x)$
is always either finite,
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(x)$
is always either finite,
![]() $\omega $
,
$\omega $
,
![]() $\omega ^*$
, or
$\omega ^*$
, or
![]() $\zeta $
.
$\zeta $
.
We often refer to the intervals that comprise a condensation of a linear order as blocks. For the finite condensation of a linear order
![]() $\mathcal {L}$
, a block is a maximal interval I such that for any two elements of I, there are only finitely many elements of
$\mathcal {L}$
, a block is a maximal interval I such that for any two elements of I, there are only finitely many elements of
![]() $\mathcal {L}$
between them. For elements a and b of
$\mathcal {L}$
between them. For elements a and b of
![]() $\mathcal {L}$
, we write
$\mathcal {L}$
, we write
![]() if the interval
if the interval
![]() $(a, b)_{\mathcal {L}}$
(equivalently, the interval
$(a, b)_{\mathcal {L}}$
(equivalently, the interval
![]() $[a, b]_{\mathcal {L}}$
) in
$[a, b]_{\mathcal {L}}$
) in
![]() $\mathcal {L}$
is infinite. For
$\mathcal {L}$
is infinite. For
![]() $a \prec _{\mathcal {L}} b$
, we have that
$a \prec _{\mathcal {L}} b$
, we have that
![]() if and only if a and b are in different blocks. See [Reference Rosenstein21, Chapter 4] for more on condensations.
if and only if a and b are in different blocks. See [Reference Rosenstein21, Chapter 4] for more on condensations.
Let C be a cohesive set. It follows from Theorem 2.7 that if
![]() $(\mathcal {L}_n : n \in \mathbb {N})$
is a uniformly computable sequence of linear orders, then
$(\mathcal {L}_n : n \in \mathbb {N})$
is a uniformly computable sequence of linear orders, then
![]() $\prod _C \mathcal {L}_n$
is again a linear order because linear orders are axiomatized by
$\prod _C \mathcal {L}_n$
is again a linear order because linear orders are axiomatized by
![]() $\Pi _1$
sentences. Likewise, if
$\Pi _1$
sentences. Likewise, if
![]() $(\mathcal {L}_n : n \in \mathbb {N})$
is a uniformly computable sequence of dense linear orders without endpoints, then
$(\mathcal {L}_n : n \in \mathbb {N})$
is a uniformly computable sequence of dense linear orders without endpoints, then
![]() $\prod _C \mathcal {L}_n$
is again a dense linear order without endpoints because dense linear orders without endpoints are axiomatized by
$\prod _C \mathcal {L}_n$
is again a dense linear order without endpoints because dense linear orders without endpoints are axiomatized by
![]() $\Pi _2$
sentences. In particular, if
$\Pi _2$
sentences. In particular, if
![]() $\mathcal {L}$
is a computable linear order, then
$\mathcal {L}$
is a computable linear order, then
![]() $\prod _C \mathcal {L}$
is a linear order; and if
$\prod _C \mathcal {L}$
is a linear order; and if
![]() $\mathcal {L}$
is a computable dense linear order without endpoints, then
$\mathcal {L}$
is a computable dense linear order without endpoints, then
![]() $\prod _C \mathcal {L}$
is a dense linear order without endpoints.
$\prod _C \mathcal {L}$
is a dense linear order without endpoints.
The case of
![]() $\mathbb {Q} = (\mathbb {Q}, <)$
is curious and deserves a digression. We have seen that if
$\mathbb {Q} = (\mathbb {Q}, <)$
is curious and deserves a digression. We have seen that if
![]() $\mathcal {A}$
is a finite structure, then
$\mathcal {A}$
is a finite structure, then
![]() $\mathcal {A} \cong \prod _C \mathcal {A}$
for every cohesive set C. For
$\mathcal {A} \cong \prod _C \mathcal {A}$
for every cohesive set C. For
![]() $\mathbb {Q}$
,
$\mathbb {Q}$
,
![]() $\prod _C \mathbb {Q}$
is a countable dense linear order without endpoints, and hence isomorphic to
$\prod _C \mathbb {Q}$
is a countable dense linear order without endpoints, and hence isomorphic to
![]() $\mathbb {Q}$
, for every cohesive set C. Thus
$\mathbb {Q}$
, for every cohesive set C. Thus
![]() $\mathbb {Q}$
is an example of an infinite computable structure with
$\mathbb {Q}$
is an example of an infinite computable structure with
![]() $\mathbb {Q} \cong \prod _C \mathbb {Q}$
for every cohesive set C. That
$\mathbb {Q} \cong \prod _C \mathbb {Q}$
for every cohesive set C. That
![]() $\mathbb {Q}$
is isomorphic to all of its cohesive powers is no accident. By combining Theorem 2.9 with the theory of Fraïssé limits (see, for example, [Reference Hodges14, Chapter 6]), we see that a uniformly locally finite ultrahomogeneous computable structure for a finite language is always isomorphic to all of its cohesive powers. Recall that a structure is locally finite if every finitely-generated substructure is finite and is uniformly locally finite if there is a function
$\mathbb {Q}$
is isomorphic to all of its cohesive powers is no accident. By combining Theorem 2.9 with the theory of Fraïssé limits (see, for example, [Reference Hodges14, Chapter 6]), we see that a uniformly locally finite ultrahomogeneous computable structure for a finite language is always isomorphic to all of its cohesive powers. Recall that a structure is locally finite if every finitely-generated substructure is finite and is uniformly locally finite if there is a function
![]() $f \colon \mathbb {N} \rightarrow \mathbb {N}$
such that every substructure generated by at most n elements has cardinality at most
$f \colon \mathbb {N} \rightarrow \mathbb {N}$
such that every substructure generated by at most n elements has cardinality at most
![]() $f(n)$
. Notice that every structure for a finite relational language is uniformly locally finite. Also recall that a structure is ultrahomogeneous if every isomorphism between two finitely-generated substructures extends to an automorphism of the whole structure.
$f(n)$
. Notice that every structure for a finite relational language is uniformly locally finite. Also recall that a structure is ultrahomogeneous if every isomorphism between two finitely-generated substructures extends to an automorphism of the whole structure.
Proposition 3.4. Let
![]() $\mathcal {A}$
be an infinite uniformly locally finite ultrahomogeneous computable structure for a finite language, and let C be cohesive. Then
$\mathcal {A}$
be an infinite uniformly locally finite ultrahomogeneous computable structure for a finite language, and let C be cohesive. Then
![]() $\mathcal {A} \cong \prod _C \mathcal {A}$
.
$\mathcal {A} \cong \prod _C \mathcal {A}$
.
Proof The structure
![]() $\mathcal {A}$
is ultrahomogeneous, so it is the Fraïssé limit of its age (i.e., the class of all finitely-generated structures embeddable into
$\mathcal {A}$
is ultrahomogeneous, so it is the Fraïssé limit of its age (i.e., the class of all finitely-generated structures embeddable into
![]() $\mathcal {A}$
). By [Reference Hodges14, Theorem 6.4.1] and its proof, the first-order theory of
$\mathcal {A}$
). By [Reference Hodges14, Theorem 6.4.1] and its proof, the first-order theory of
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\aleph _0$
-categorical and is axiomatized by a set T of
$\aleph _0$
-categorical and is axiomatized by a set T of
![]() $\Pi _2$
sentences. Thus if
$\Pi _2$
sentences. Thus if
![]() $\mathcal {B}$
is any countable model of T, then
$\mathcal {B}$
is any countable model of T, then
![]() $\mathcal {A} \cong \mathcal {B}$
. We have that
$\mathcal {A} \cong \mathcal {B}$
. We have that
![]() $\prod _C \mathcal {A} \models T$
by Theorem 2.9 item (2), so
$\prod _C \mathcal {A} \models T$
by Theorem 2.9 item (2), so
![]() $\mathcal {A} \cong \prod _C \mathcal {A}$
.
$\mathcal {A} \cong \prod _C \mathcal {A}$
.
Proposition 3.4 implies that if a uniformly locally finite computable structure for a finite language is a Fraïssé limit, then it is isomorphic to all of its cohesive powers. Thus computable presentations of the Rado graph and the countable atomless Boolean algebra are additional examples of computable structures that are isomorphic to all of their cohesive powers. Examples of this phenomenon that cannot be attributed to ultrahomogeneity appear in Sections 4 and 5.
Returning to linear orders, it is helpful to recall the following well-known lemma stating that a strictly order-preserving surjection from one linear order onto another is necessarily an isomorphism.
Lemma 3.5. Let
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
and
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
and
![]() $\mathcal {M} = (M, \prec _{\mathcal {M}})$
be linear orders. If
$\mathcal {M} = (M, \prec _{\mathcal {M}})$
be linear orders. If
![]() $f \colon L \rightarrow M$
is surjective and satisfies
$f \colon L \rightarrow M$
is surjective and satisfies
![]() $(\forall x, y \in L)(x \prec _{\mathcal {L}} y \;\rightarrow \; f(x) \prec _{\mathcal {M}} f(y))$
, then f is an isomorphism.
$(\forall x, y \in L)(x \prec _{\mathcal {L}} y \;\rightarrow \; f(x) \prec _{\mathcal {M}} f(y))$
, then f is an isomorphism.
Cohesive powers commute with sums, products, and reverses.
Theorem 3.6. Let
![]() $\mathcal {L}_0$
and
$\mathcal {L}_0$
and
![]() $\mathcal {L}_1$
be computable linear orders, and let C be cohesive. Then
$\mathcal {L}_1$
be computable linear orders, and let C be cohesive. Then
![]() $:$
$:$
-
(1)
 $\prod _C(\mathcal {L}_0 + \mathcal {L}_1) \cong \prod _C\mathcal {L}_0 + \prod _C\mathcal {L}_1$
,
$\prod _C(\mathcal {L}_0 + \mathcal {L}_1) \cong \prod _C\mathcal {L}_0 + \prod _C\mathcal {L}_1$
, -
(2)
 $\prod _C(\mathcal {L}_0\mathcal {L}_1) \cong \bigl ( \prod _C\mathcal {L}_0 \bigr ) \bigl ( \prod _C\mathcal {L}_1\bigr )$
, and
$\prod _C(\mathcal {L}_0\mathcal {L}_1) \cong \bigl ( \prod _C\mathcal {L}_0 \bigr ) \bigl ( \prod _C\mathcal {L}_1\bigr )$
, and -
(3)
 $\prod _C(\mathcal {L}_0^*) \cong \bigl ( \prod _C\mathcal {L}_0 \bigr )^*$
.
$\prod _C(\mathcal {L}_0^*) \cong \bigl ( \prod _C\mathcal {L}_0 \bigr )^*$
.
Proof We give proofs in the style of that of Theorem 2.20. For alternate proofs, see [Reference Dimitrov, Harizanov, Morozov, Shafer, Soskova, Vatev, Manea, Martin, Paulusma and Primiero9, Theorem 6].
For (1), let
![]() $\mathcal {M} = \mathcal {L}_0 + \mathcal {L}_1$
. Expand the disjoint union
$\mathcal {M} = \mathcal {L}_0 + \mathcal {L}_1$
. Expand the disjoint union
![]() $\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
by adding unary relation symbols
$\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
by adding unary relation symbols
![]() $L_0$
,
$L_0$
,
![]() $L_1$
, and M that are interpreted as
$L_1$
, and M that are interpreted as
![]() $|\mathcal {L}_0|$
,
$|\mathcal {L}_0|$
,
![]() $|\mathcal {L}_1|$
, and
$|\mathcal {L}_1|$
, and
![]() $|\mathcal {M}|$
; and by adding a
$|\mathcal {M}|$
; and by adding a
![]() $2$
-ary relation symbol
$2$
-ary relation symbol
![]() $R_f$
that is interpreted as the graph of the function
$R_f$
that is interpreted as the graph of the function
![]() $f \colon |\mathcal {L}_0 \sqcup \mathcal {L}_1| \rightarrow |\mathcal {M}|$
inside
$f \colon |\mathcal {L}_0 \sqcup \mathcal {L}_1| \rightarrow |\mathcal {M}|$
inside
![]() $\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
given by
$\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
given by
for each
![]() $i < 2$
. In
$i < 2$
. In
![]() $\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
, the
$\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
, the
![]() $\prec $
relation is a linear order when restricted to
$\prec $
relation is a linear order when restricted to
![]() $|\mathcal {L}_0|$
,
$|\mathcal {L}_0|$
,
![]() $|\mathcal {L}_1|$
, or
$|\mathcal {L}_1|$
, or
![]() $|\mathcal {M}|$
. Furthermore,
$|\mathcal {M}|$
. Furthermore,
![]() $R_f$
is the graph of a function f from
$R_f$
is the graph of a function f from
![]() $|\mathcal {L}_0 \sqcup \mathcal {L}_1|$
onto
$|\mathcal {L}_0 \sqcup \mathcal {L}_1|$
onto
![]() $|\mathcal {M}|$
with the following properties, which together witness that
$|\mathcal {M}|$
with the following properties, which together witness that
![]() $\mathcal {M} \cong \mathcal {L}_0 + \mathcal {L}_1$
as linear orders.
$\mathcal {M} \cong \mathcal {L}_0 + \mathcal {L}_1$
as linear orders.
-
•
 $\forall x \forall y\, [(L_0(x) \,\wedge \, L_0(y) \,\wedge \, x \prec y) \;\rightarrow \; f(x) \prec f(y)]$
.
$\forall x \forall y\, [(L_0(x) \,\wedge \, L_0(y) \,\wedge \, x \prec y) \;\rightarrow \; f(x) \prec f(y)]$
. -
•
 $\forall x \forall y\, [(L_1(x) \,\wedge \, L_1(y) \,\wedge \, x \prec y) \;\rightarrow \; f(x) \prec f(y)]$
.
$\forall x \forall y\, [(L_1(x) \,\wedge \, L_1(y) \,\wedge \, x \prec y) \;\rightarrow \; f(x) \prec f(y)]$
. -
•
 $\forall x \forall y\, [(L_0(x) \,\wedge \, L_1(y)) \;\rightarrow \; f(x) \prec f(y)]$
.
$\forall x \forall y\, [(L_0(x) \,\wedge \, L_1(y)) \;\rightarrow \; f(x) \prec f(y)]$
.
All of the above is expressible by a
![]() $\Pi _2$
sentence. By Proposition 2.12, the substructures of
$\Pi _2$
sentence. By Proposition 2.12, the substructures of
![]() $\prod _C(\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M})$
corresponding to
$\prod _C(\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M})$
corresponding to
![]() $L_0$
,
$L_0$
,
![]() $L_1$
, and M are isomorphic to
$L_1$
, and M are isomorphic to
![]() $\prod _C \mathcal {L}_0$
,
$\prod _C \mathcal {L}_0$
,
![]() $\prod _C \mathcal {L}_1$
, and
$\prod _C \mathcal {L}_1$
, and
![]() $\prod _C \mathcal {M}$
. By Theorem 2.9 item (2),
$\prod _C \mathcal {M}$
. By Theorem 2.9 item (2),
![]() $\prod _C \mathcal {L}_0$
,
$\prod _C \mathcal {L}_0$
,
![]() $\prod _C \mathcal {L}_1$
, and
$\prod _C \mathcal {L}_1$
, and
![]() $\prod _C \mathcal {M}$
are linear orders as
$\prod _C \mathcal {M}$
are linear orders as
![]() $\{\prec \}$
-structures, and
$\{\prec \}$
-structures, and
![]() $R_f^{\prod _C(\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M})}$
yields a function from
$R_f^{\prod _C(\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M})}$
yields a function from
![]() $|\prod _C \mathcal {L}_0 \sqcup \prod _C \mathcal {L}_1|$
onto
$|\prod _C \mathcal {L}_0 \sqcup \prod _C \mathcal {L}_1|$
onto
![]() $|\prod _C \mathcal {M}|$
witnessing that
$|\prod _C \mathcal {M}|$
witnessing that
![]() $\prod _C \mathcal {M} \cong \prod _C \mathcal {L}_0 + \prod _C \mathcal {L}_1$
as linear orders. Thus
$\prod _C \mathcal {M} \cong \prod _C \mathcal {L}_0 + \prod _C \mathcal {L}_1$
as linear orders. Thus
![]() $\prod _C(\mathcal {L}_0 + \mathcal {L}_1) \cong \prod _C\mathcal {L}_0 + \prod _C\mathcal {L}_1$
.
$\prod _C(\mathcal {L}_0 + \mathcal {L}_1) \cong \prod _C\mathcal {L}_0 + \prod _C\mathcal {L}_1$
.
For (2), let
![]() $\mathcal {M} = \mathcal {L}_0 \mathcal {L}_1$
. Expand the disjoint union
$\mathcal {M} = \mathcal {L}_0 \mathcal {L}_1$
. Expand the disjoint union
![]() $\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
by adding unary relation symbols
$\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
by adding unary relation symbols
![]() $L_0$
,
$L_0$
,
![]() $L_1$
, and M that are interpreted as
$L_1$
, and M that are interpreted as
![]() $|\mathcal {L}_0|$
,
$|\mathcal {L}_0|$
,
![]() $|\mathcal {L}_1|$
, and
$|\mathcal {L}_1|$
, and
![]() $|\mathcal {M}|$
; and by adding a
$|\mathcal {M}|$
; and by adding a
![]() $3$
-ary relation symbol
$3$
-ary relation symbol
![]() $R_f$
that is interpreted as the graph of the function
$R_f$
that is interpreted as the graph of the function
![]() $f \colon |\mathcal {L}_1| \times |\mathcal {L}_0| \rightarrow |\mathcal {M}|$
inside
$f \colon |\mathcal {L}_1| \times |\mathcal {L}_0| \rightarrow |\mathcal {M}|$
inside
![]() $\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
given by
$\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
given by
In
![]() $\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
, the
$\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M}$
, the
![]() $\prec $
relation is a linear order when restricted to
$\prec $
relation is a linear order when restricted to
![]() $|\mathcal {L}_0|$
,
$|\mathcal {L}_0|$
,
![]() $|\mathcal {L}_1|$
, or
$|\mathcal {L}_1|$
, or
![]() $|\mathcal {M}|$
. Furthermore,
$|\mathcal {M}|$
. Furthermore,
![]() $R_f$
is the graph of a function f from
$R_f$
is the graph of a function f from
![]() $|\mathcal {L}_1| \times |\mathcal {L}_0|$
onto
$|\mathcal {L}_1| \times |\mathcal {L}_0|$
onto
![]() $|\mathcal {M}|$
with the following property, which witnesses that
$|\mathcal {M}|$
with the following property, which witnesses that
![]() $\mathcal {M} \cong \mathcal {L}_0 \mathcal {L}_1$
as linear orders.
$\mathcal {M} \cong \mathcal {L}_0 \mathcal {L}_1$
as linear orders.
 $$ \begin{align*} \forall a \forall b \forall x \forall y \, \biggl[\Bigl(L_0(a) &\,\wedge\, L_0(b) \,\wedge\, L_1(x) \,\wedge\, L_1(y)\Bigr) \;\rightarrow\\&\Bigl( f(x,a) \prec f(y,b) \;\;\leftrightarrow\;\; \bigl( x \prec y \;\vee\; (x = y \,\wedge\, a \prec b) \bigr) \Bigr)\biggr]. \end{align*} $$
$$ \begin{align*} \forall a \forall b \forall x \forall y \, \biggl[\Bigl(L_0(a) &\,\wedge\, L_0(b) \,\wedge\, L_1(x) \,\wedge\, L_1(y)\Bigr) \;\rightarrow\\&\Bigl( f(x,a) \prec f(y,b) \;\;\leftrightarrow\;\; \bigl( x \prec y \;\vee\; (x = y \,\wedge\, a \prec b) \bigr) \Bigr)\biggr]. \end{align*} $$
All of the above is expressible by a
![]() $\Pi _2$
sentence. By Proposition 2.12, the substructures of
$\Pi _2$
sentence. By Proposition 2.12, the substructures of
![]() $\prod _C(\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M})$
corresponding to
$\prod _C(\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M})$
corresponding to
![]() $L_0$
,
$L_0$
,
![]() $L_1$
, and M are isomorphic to
$L_1$
, and M are isomorphic to
![]() $\prod _C \mathcal {L}_0$
,
$\prod _C \mathcal {L}_0$
,
![]() $\prod _C \mathcal {L}_1$
, and
$\prod _C \mathcal {L}_1$
, and
![]() $\prod _C \mathcal {M}$
. By Theorem 2.9 item (2),
$\prod _C \mathcal {M}$
. By Theorem 2.9 item (2),
![]() $\prod _C \mathcal {L}_0$
,
$\prod _C \mathcal {L}_0$
,
![]() $\prod _C \mathcal {L}_1$
, and
$\prod _C \mathcal {L}_1$
, and
![]() $\prod _C \mathcal {M}$
are linear orders as
$\prod _C \mathcal {M}$
are linear orders as
![]() $\{\prec \}$
-structures, and
$\{\prec \}$
-structures, and
![]() $R_f^{\prod _C(\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M})}$
yields a function from
$R_f^{\prod _C(\mathcal {L}_0 \sqcup \mathcal {L}_1 \sqcup \mathcal {M})}$
yields a function from
![]() $|\prod _C \mathcal {L}_1| \times |\prod _C \mathcal {L}_0|$
onto
$|\prod _C \mathcal {L}_1| \times |\prod _C \mathcal {L}_0|$
onto
![]() $|\prod _C \mathcal {M}|$
witnessing that
$|\prod _C \mathcal {M}|$
witnessing that
![]() $\prod _C \mathcal {M} \cong \bigl ( \prod _C \mathcal {L}_0 \bigr ) \bigl ( \prod _C \mathcal {L}_1 \bigr )$
as linear orders. Thus
$\prod _C \mathcal {M} \cong \bigl ( \prod _C \mathcal {L}_0 \bigr ) \bigl ( \prod _C \mathcal {L}_1 \bigr )$
as linear orders. Thus
![]() $\prod _C(\mathcal {L}_0 \mathcal {L}_1) \cong \bigl ( \prod _C \mathcal {L}_0 \bigr ) \bigl ( \prod _C \mathcal {L}_1 \bigr )$
.
$\prod _C(\mathcal {L}_0 \mathcal {L}_1) \cong \bigl ( \prod _C \mathcal {L}_0 \bigr ) \bigl ( \prod _C \mathcal {L}_1 \bigr )$
.
For (3), let
![]() $\mathcal {M} = \mathcal {L}_0^*$
. Expand the disjoint union
$\mathcal {M} = \mathcal {L}_0^*$
. Expand the disjoint union
![]() $\mathcal {L}_0 \sqcup \mathcal {M}$
by adding unary relation symbols
$\mathcal {L}_0 \sqcup \mathcal {M}$
by adding unary relation symbols
![]() $L_0$
and M that are interpreted as
$L_0$
and M that are interpreted as
![]() $|\mathcal {L}_0|$
and
$|\mathcal {L}_0|$
and
![]() $|\mathcal {M}|$
; and by adding a
$|\mathcal {M}|$
; and by adding a
![]() $2$
-ary relation symbol
$2$
-ary relation symbol
![]() $R_f$
that is interpreted as the graph of the function
$R_f$
that is interpreted as the graph of the function
![]() $f \colon |\mathcal {L}_0| \rightarrow |\mathcal {M}|$
inside
$f \colon |\mathcal {L}_0| \rightarrow |\mathcal {M}|$
inside
![]() $\mathcal {L}_0 \sqcup \mathcal {M}$
given by
$\mathcal {L}_0 \sqcup \mathcal {M}$
given by
![]() $f(\langle 0, x \rangle ) = \langle 1, x \rangle $
. In
$f(\langle 0, x \rangle ) = \langle 1, x \rangle $
. In
![]() $\mathcal {L}_0 \sqcup \mathcal {M}$
, the
$\mathcal {L}_0 \sqcup \mathcal {M}$
, the
![]() $\prec $
relation is a linear order when restricted to
$\prec $
relation is a linear order when restricted to
![]() $|\mathcal {L}_0|$
or
$|\mathcal {L}_0|$
or
![]() $|\mathcal {M}|$
, and
$|\mathcal {M}|$
, and
![]() $R_f$
is the graph of a function f from
$R_f$
is the graph of a function f from
![]() $|\mathcal {L}_0|$
onto
$|\mathcal {L}_0|$
onto
![]() $|\mathcal {M}|$
such that
$|\mathcal {M}|$
such that
which witnesses that
![]() $\mathcal {M} \cong \mathcal {L}_0^*$
as linear orders. All of the above is expressible by a
$\mathcal {M} \cong \mathcal {L}_0^*$
as linear orders. All of the above is expressible by a
![]() $\Pi _2$
sentence. By Proposition 2.12, the substructures of
$\Pi _2$
sentence. By Proposition 2.12, the substructures of
![]() $\prod _C(\mathcal {L}_0 \sqcup \mathcal {M})$
corresponding to
$\prod _C(\mathcal {L}_0 \sqcup \mathcal {M})$
corresponding to
![]() $L_0$
and M are isomorphic to
$L_0$
and M are isomorphic to
![]() $\prod _C \mathcal {L}_0$
and
$\prod _C \mathcal {L}_0$
and
![]() $\prod _C \mathcal {M}$
. By Theorem 2.9 item (2),
$\prod _C \mathcal {M}$
. By Theorem 2.9 item (2),
![]() $\prod _C \mathcal {L}_0$
and
$\prod _C \mathcal {L}_0$
and
![]() $\prod _C \mathcal {M}$
are linear orders as
$\prod _C \mathcal {M}$
are linear orders as
![]() $\{\prec \}$
-structures, and
$\{\prec \}$
-structures, and
![]() $R_f^{\prod _C(\mathcal {L}_0 \sqcup \mathcal {M})}$
yields a function from
$R_f^{\prod _C(\mathcal {L}_0 \sqcup \mathcal {M})}$
yields a function from
![]() $|\prod _C \mathcal {L}_0|$
onto
$|\prod _C \mathcal {L}_0|$
onto
![]() $|\prod _C \mathcal {M}|$
witnessing that
$|\prod _C \mathcal {M}|$
witnessing that
![]() $\prod _C \mathcal {M} \cong \bigl ( \prod _C \mathcal {L}_0 \bigr )^*$
as linear orders. Thus
$\prod _C \mathcal {M} \cong \bigl ( \prod _C \mathcal {L}_0 \bigr )^*$
as linear orders. Thus
![]() $\prod _C(\mathcal {L}_0^*) \cong \bigl ( \prod _C \mathcal {L}_0 \bigr )^*$
.
$\prod _C(\mathcal {L}_0^*) \cong \bigl ( \prod _C \mathcal {L}_0 \bigr )^*$
.
Sections 4–6 concern calculating the order-types of cohesive powers of computable copies of
![]() $\omega $
. To do this, we must be able to determine when one element of a cohesive power is an immediate successor or immediate predecessor of another, and we must be able to determine when two elements of a cohesive power are in different blocks of its finite condensation.
$\omega $
. To do this, we must be able to determine when one element of a cohesive power is an immediate successor or immediate predecessor of another, and we must be able to determine when two elements of a cohesive power are in different blocks of its finite condensation.
In a cohesive power
![]() $\prod _C \mathcal {L}$
of a computable linear order
$\prod _C \mathcal {L}$
of a computable linear order
![]() $\mathcal {L}$
,
$\mathcal {L}$
,
![]() $[\varphi ]$
is the immediate successor of
$[\varphi ]$
is the immediate successor of
![]() $[\psi ]$
if and only if
$[\psi ]$
if and only if
![]() $\varphi (n)$
is the immediate successor of
$\varphi (n)$
is the immediate successor of
![]() $\psi (n)$
for almost every
$\psi (n)$
for almost every
![]() $n \in C$
. Therefore also
$n \in C$
. Therefore also
![]() $[\psi ]$
is the immediate predecessor of
$[\psi ]$
is the immediate predecessor of
![]() $[\varphi ]$
if and only if
$[\varphi ]$
if and only if
![]() $\psi (n)$
is the immediate predecessor of
$\psi (n)$
is the immediate predecessor of
![]() $\varphi (n)$
for almost every
$\varphi (n)$
for almost every
![]() $n \in C$
.
$n \in C$
.
Lemma 3.7. Let
![]() $(\mathcal {L}_n : n \in \mathbb {N})$
be a uniformly computable sequence of linear orders, let C be cohesive, and let
$(\mathcal {L}_n : n \in \mathbb {N})$
be a uniformly computable sequence of linear orders, let C be cohesive, and let
![]() $[\psi ]$
and
$[\psi ]$
and
![]() $[\varphi ]$
be elements of
$[\varphi ]$
be elements of
![]() $\prod _C \mathcal {L}_n$
. Then the following are equivalent.
$\prod _C \mathcal {L}_n$
. Then the following are equivalent.
-
(1)
 $[\varphi ]$
is the
$[\varphi ]$
is the
 $\prec _{\prod _C \mathcal {L}_n}$
-immediate successor of
$\prec _{\prod _C \mathcal {L}_n}$
-immediate successor of
 $[\psi ]$
.
$[\psi ]$
. -
(2)
 $(\forall ^\infty n \in C)(\varphi (n)\text { is the }\prec _{\mathcal {L}_n}\text {-immediate successor of } \psi (n))$
.
$(\forall ^\infty n \in C)(\varphi (n)\text { is the }\prec _{\mathcal {L}_n}\text {-immediate successor of } \psi (n))$
. -
(3)
 $(\exists ^\infty n \in C)(\varphi (n)\text { is the }\prec _{\mathcal {L}_n}\text {-immediate successor of } \psi (n))$
.
$(\exists ^\infty n \in C)(\varphi (n)\text { is the }\prec _{\mathcal {L}_n}\text {-immediate successor of } \psi (n))$
.
Proof That x is the
![]() $\prec $
-immediate successor of y is a
$\prec $
-immediate successor of y is a
![]() $\Pi _1$
property of x and y. Therefore items (1) and (2) are equivalent by Theorem 2.7 item (3). The set
$\Pi _1$
property of x and y. Therefore items (1) and (2) are equivalent by Theorem 2.7 item (3). The set
is the intersection of a c.e. set and a co-c.e. set, so items (2) and (3) are equivalent by cohesiveness.
Lemma 3.8. Let
![]() $(\mathcal {L}_n : n \in \mathbb {N})$
be a uniformly computable sequence of linear orders, let C be cohesive, and let
$(\mathcal {L}_n : n \in \mathbb {N})$
be a uniformly computable sequence of linear orders, let C be cohesive, and let
![]() $[\psi ]$
and
$[\psi ]$
and
![]() $[\varphi ]$
be elements of
$[\varphi ]$
be elements of
![]() $\prod _C \mathcal {L}_n$
. Then the following are equivalent.
$\prod _C \mathcal {L}_n$
. Then the following are equivalent.
-
(1)
 .
. -
(2)
 $\lim _{n \in C}|(\psi (n), \varphi (n))_{\mathcal {L}_n}| = \infty $
.
$\lim _{n \in C}|(\psi (n), \varphi (n))_{\mathcal {L}_n}| = \infty $
. -
(3)
 $\limsup _{n \in C}|(\psi (n), \varphi (n))_{\mathcal {L}_n}| = \infty $
.
$\limsup _{n \in C}|(\psi (n), \varphi (n))_{\mathcal {L}_n}| = \infty $
.
Proof We show that the following are equivalent for each fixed
![]() $k \in \mathbb {N}$
.
$k \in \mathbb {N}$
.
-
(i)
 $|([\psi ], [\varphi ])_{\prod _C \mathcal {L}_n}| \geq k$
.
$|([\psi ], [\varphi ])_{\prod _C \mathcal {L}_n}| \geq k$
. -
(ii)
 $(\forall ^\infty n \in C)(|(\psi (n), \varphi (n))_{\mathcal {L}_n}| \geq k)$
.
$(\forall ^\infty n \in C)(|(\psi (n), \varphi (n))_{\mathcal {L}_n}| \geq k)$
. -
(iii)
 $(\exists ^\infty n \in C)(|(\psi (n), \varphi (n))_{\mathcal {L}_n}| \geq k)$
.
$(\exists ^\infty n \in C)(|(\psi (n), \varphi (n))_{\mathcal {L}_n}| \geq k)$
.
That an interval
![]() $(x,y)$
in a linear order contains at least k distinct elements for a fixed k is a
$(x,y)$
in a linear order contains at least k distinct elements for a fixed k is a
![]() $\Sigma _1$
property of x and y. Therefore items (i) and (ii) are equivalent by Theorem 2.7 item (3). The set
$\Sigma _1$
property of x and y. Therefore items (i) and (ii) are equivalent by Theorem 2.7 item (3). The set
![]() $\{n : |(\psi (n), \varphi (n))_{\mathcal {L}_n}| \geq k\}$
is c.e., so items (ii) and (iii) are equivalent by cohesiveness.
$\{n : |(\psi (n), \varphi (n))_{\mathcal {L}_n}| \geq k\}$
is c.e., so items (ii) and (iii) are equivalent by cohesiveness.
It now follows that items (1)–(3) are equivalent. Item (1) holds if and only if item (i) holds for every k; item (2) holds if and only if item (ii) holds for every k; and item (3) holds if and only if item (iii) holds for every k.
The finite condensation of a cohesive product of computable linear orders by a co-c.e. cohesive set is always dense.
Theorem 3.9. Let
![]() $(\mathcal {L}_n : n \in \mathbb {N})$
be a uniformly computable sequence of linear orders, and let C be a cohesive set. If either
$(\mathcal {L}_n : n \in \mathbb {N})$
be a uniformly computable sequence of linear orders, and let C be a cohesive set. If either
![]() $(\mathcal {L}_n : n \in \mathbb {N})$
is uniformly
$(\mathcal {L}_n : n \in \mathbb {N})$
is uniformly
![]() $1$
-decidable or C is co-c.e., then
$1$
-decidable or C is co-c.e., then
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\prod _C \mathcal {L}_n)$
is dense.
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\prod _C \mathcal {L}_n)$
is dense.
Proof The cohesive product
![]() $\prod _C \mathcal {L}_n$
is
$\prod _C \mathcal {L}_n$
is
![]() $\Sigma _1$
-recursively saturated by Theorem 2.16 item (2) in the uniformly
$\Sigma _1$
-recursively saturated by Theorem 2.16 item (2) in the uniformly
![]() $1$
-decidable case and by Corollary 2.19 item (1) in the co-c.e. case. Thus it suffices to show that if
$1$
-decidable case and by Corollary 2.19 item (1) in the co-c.e. case. Thus it suffices to show that if
![]() $\mathcal {M} = (M, \prec _{\mathcal {M}})$
is a
$\mathcal {M} = (M, \prec _{\mathcal {M}})$
is a
![]() $\Sigma _1$
-recursively saturated linear order, then
$\Sigma _1$
-recursively saturated linear order, then
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\mathcal {M})$
is dense. To see this, let
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\mathcal {M})$
is dense. To see this, let
![]() $a, b \in M$
be such that
$a, b \in M$
be such that
![]() . For each
. For each
![]() $k \in \mathbb {N}$
, let
$k \in \mathbb {N}$
, let
![]() $\Phi _k(x; a, b)$
be the following formula (with parameters a and b) expressing that there are at least k elements between a and x and at least k elements between x and b:
$\Phi _k(x; a, b)$
be the following formula (with parameters a and b) expressing that there are at least k elements between a and x and at least k elements between x and b:
Let
![]() $p(x) = \{\Phi _k(x; a, b) : k \in \mathbb {N}\}$
. Then
$p(x) = \{\Phi _k(x; a, b) : k \in \mathbb {N}\}$
. Then
![]() $p(x)$
is a computable set of
$p(x)$
is a computable set of
![]() $\Sigma _1$
formulas. Furthermore,
$\Sigma _1$
formulas. Furthermore,
![]() $p(x)$
is a type over
$p(x)$
is a type over
![]() $\mathcal {M}$
because the interval
$\mathcal {M}$
because the interval
![]() $(a,b)_{\mathcal {M}}$
is infinite. Therefore
$(a,b)_{\mathcal {M}}$
is infinite. Therefore
![]() $p(x)$
is realized by some
$p(x)$
is realized by some
![]() $c \in M$
because
$c \in M$
because
![]() $\mathcal {M}$
is
$\mathcal {M}$
is
![]() $\Sigma _1$
-recursively saturated. Thus the intervals
$\Sigma _1$
-recursively saturated. Thus the intervals
![]() $(a, c)_{\mathcal {M}}$
and
$(a, c)_{\mathcal {M}}$
and
![]() $(c, b)_{\mathcal {M}}$
are both infinite, so
$(c, b)_{\mathcal {M}}$
are both infinite, so
![]() . It follows that
. It follows that
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\mathcal {M})$
is dense.
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\mathcal {M})$
is dense.
4 Cohesive powers of computable copies of
 $\omega $
$\omega $
We investigate the cohesive powers of computable linear orders of type
![]() $\omega $
. Observe that an infinite linear order has type
$\omega $
. Observe that an infinite linear order has type
![]() $\omega $
if and only if every element has only finitely many predecessors. We rely on this characterization throughout. Though not part of the language of linear orders, every linear order
$\omega $
if and only if every element has only finitely many predecessors. We rely on this characterization throughout. Though not part of the language of linear orders, every linear order
![]() $\mathcal {L}$
has an associated immediate successor relation
$\mathcal {L}$
has an associated immediate successor relation
![]() $S^{\mathcal {L}} \subseteq |\mathcal {L}| \times |\mathcal {L}|$
, where
$S^{\mathcal {L}} \subseteq |\mathcal {L}| \times |\mathcal {L}|$
, where
![]() $S^{\mathcal {L}}(a, b)$
holds for
$S^{\mathcal {L}}(a, b)$
holds for
![]() $a, b \in |\mathcal {L}|$
if and only if b is the
$a, b \in |\mathcal {L}|$
if and only if b is the
![]() $\prec _{\mathcal {L}}$
-immediate successor of a. As explained in [Reference Moses19, Section 3], a computable linear order
$\prec _{\mathcal {L}}$
-immediate successor of a. As explained in [Reference Moses19, Section 3], a computable linear order
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
![]() $1$
-decidable if and only if the immediate successor relation
$1$
-decidable if and only if the immediate successor relation
![]() $S^{\mathcal {L}}$
is computable. It is straightforward to check that a computable copy
$S^{\mathcal {L}}$
is computable. It is straightforward to check that a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
is computably isomorphic to the usual presentation
$\omega $
is computably isomorphic to the usual presentation
![]() $(\mathbb {N}, <)$
if and only if
$(\mathbb {N}, <)$
if and only if
![]() $S^{\mathcal {L}}$
is computable. Thus the computable copies of
$S^{\mathcal {L}}$
is computable. Thus the computable copies of
![]() $\omega $
that are computably isomorphic to the usual presentation are exactly the
$\omega $
that are computably isomorphic to the usual presentation are exactly the
![]() $1$
-decidable copies of
$1$
-decidable copies of
![]() $\omega $
.
$\omega $
.
We show that if
![]() $\mathcal {L}$
is a computable copy of
$\mathcal {L}$
is a computable copy of
![]() $\omega $
that is computably isomorphic to the usual presentation, then every cohesive power of
$\omega $
that is computably isomorphic to the usual presentation, then every cohesive power of
![]() $\mathcal {L}$
has order-type
$\mathcal {L}$
has order-type
![]() $\omega + \zeta \eta $
(Theorem 4.5). This is to be expected because
$\omega + \zeta \eta $
(Theorem 4.5). This is to be expected because
![]() $\omega + \zeta \eta $
is familiar as the order-type of every countable non-standard model of Peano arithmetic (see [Reference Kaye15, Theorem 6.4]). However, being computably isomorphic to the usual presentation is not a characterization of the computable copies of
$\omega + \zeta \eta $
is familiar as the order-type of every countable non-standard model of Peano arithmetic (see [Reference Kaye15, Theorem 6.4]). However, being computably isomorphic to the usual presentation is not a characterization of the computable copies of
![]() $\omega $
having cohesive powers of order-type
$\omega $
having cohesive powers of order-type
![]() $\omega + \zeta \eta $
. We show that there is a computable copy of
$\omega + \zeta \eta $
. We show that there is a computable copy of
![]() $\omega $
that is not computably isomorphic to the usual presentation, yet still has every cohesive power isomorphic to
$\omega $
that is not computably isomorphic to the usual presentation, yet still has every cohesive power isomorphic to
![]() $\omega + \zeta \eta $
(Theorem 4.7). Thus to compute a copy of
$\omega + \zeta \eta $
(Theorem 4.7). Thus to compute a copy of
![]() $\omega $
having a cohesive power not of type
$\omega $
having a cohesive power not of type
![]() $\omega + \zeta \eta $
, one must do more than simply arrange for the immediate successor relation to be non-computable. We show that for every cohesive set C, there is a computable copy
$\omega + \zeta \eta $
, one must do more than simply arrange for the immediate successor relation to be non-computable. We show that for every cohesive set C, there is a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
such that the cohesive power
$\omega $
such that the cohesive power
![]() $\prod _C \mathcal {L}$
does not have order-type
$\prod _C \mathcal {L}$
does not have order-type
![]() $\omega + \zeta \eta $
(Theorem 4.8). However, we also show that whenever
$\omega + \zeta \eta $
(Theorem 4.8). However, we also show that whenever
![]() $\mathcal {L}$
is a computable copy of
$\mathcal {L}$
is a computable copy of
![]() $\omega $
and C is a co-c.e. cohesive set, the finite condensation
$\omega $
and C is a co-c.e. cohesive set, the finite condensation
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\prod _C \mathcal {L})$
of the cohesive power
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\prod _C \mathcal {L})$
of the cohesive power
![]() $\prod _C \mathcal {L}$
always has order-type
$\prod _C \mathcal {L}$
always has order-type
![]() $\boldsymbol {1} + \eta $
(Theorem 4.4).
$\boldsymbol {1} + \eta $
(Theorem 4.4).
First, a cohesive power of a computable copy of
![]() $\omega $
always has an initial segment of order-type
$\omega $
always has an initial segment of order-type
![]() $\omega $
.
$\omega $
.
Lemma 4.1. Let
![]() $\mathcal {L}$
be a computable copy of
$\mathcal {L}$
be a computable copy of
![]() $\omega $
, and let C be cohesive. Then the image of the canonical embedding of
$\omega $
, and let C be cohesive. Then the image of the canonical embedding of
![]() $\mathcal {L}$
into
$\mathcal {L}$
into
![]() $\prod _C \mathcal {L}$
is an initial segment of
$\prod _C \mathcal {L}$
is an initial segment of
![]() $\prod _C \mathcal {L}$
of order-type
$\prod _C \mathcal {L}$
of order-type
![]() $\omega $
.
$\omega $
.
Proof Let
![]() $a_0 \prec _{\mathcal {L}} a_1 \prec _{\mathcal {L}} a_2 \prec _{\mathcal {L}} \ldots $
be the (not necessarily computable) listing of
$a_0 \prec _{\mathcal {L}} a_1 \prec _{\mathcal {L}} a_2 \prec _{\mathcal {L}} \ldots $
be the (not necessarily computable) listing of
![]() $|\mathcal {L}|$
in
$|\mathcal {L}|$
in
![]() $\prec _{\mathcal {L}}$
-increasing order. The image of the canonical embedding consists of those elements of the form
$\prec _{\mathcal {L}}$
-increasing order. The image of the canonical embedding consists of those elements of the form
![]() $[\psi _{a_k}]$
, where
$[\psi _{a_k}]$
, where
![]() $\psi _{a_k}$
is the total computable function with constant value
$\psi _{a_k}$
is the total computable function with constant value
![]() $a_k$
.
$a_k$
.
For each
![]() $k \in \mathbb {N}$
, we have that
$k \in \mathbb {N}$
, we have that
![]() $\mathcal {L} \models \exists ^{= k} x\, (x \prec _{\mathcal {L}} a_k)$
and therefore that
$\mathcal {L} \models \exists ^{= k} x\, (x \prec _{\mathcal {L}} a_k)$
and therefore that
![]() $(\forall ^\infty n \in C)(\exists ^{= k} x)(x \prec _{\mathcal {L}} \psi _{a_k}(n))$
. Thus also
$(\forall ^\infty n \in C)(\exists ^{= k} x)(x \prec _{\mathcal {L}} \psi _{a_k}(n))$
. Thus also
![]() $\prod _C \mathcal {L} \models (\exists ^{= k} x)(x \prec _{\prod _C \mathcal {L}} [\psi _{a_k}])$
by Theorem 2.9 item (1). That is, for each
$\prod _C \mathcal {L} \models (\exists ^{= k} x)(x \prec _{\prod _C \mathcal {L}} [\psi _{a_k}])$
by Theorem 2.9 item (1). That is, for each
![]() $k \in \mathbb {N}$
, there are exactly k many elements of
$k \in \mathbb {N}$
, there are exactly k many elements of
![]() $\prod _C \mathcal {L}$
that are
$\prod _C \mathcal {L}$
that are
![]() $\prec _{\prod _C \mathcal {L}}$
-below
$\prec _{\prod _C \mathcal {L}}$
-below
![]() $[\psi _{a_k}]$
. Thus
$[\psi _{a_k}]$
. Thus
![]() $[\psi _{a_0}] \prec _{\prod _C \mathcal {L}} [\psi _{a_1}] \prec _{\prod _C \mathcal {L}} \cdots $
is an initial segment of
$[\psi _{a_0}] \prec _{\prod _C \mathcal {L}} [\psi _{a_1}] \prec _{\prod _C \mathcal {L}} \cdots $
is an initial segment of
![]() $\prod _C \mathcal {L}$
of order-type
$\prod _C \mathcal {L}$
of order-type
![]() $\omega $
.
$\omega $
.
Let
![]() $\mathcal {L}$
be a computable copy of
$\mathcal {L}$
be a computable copy of
![]() $\omega $
, let C be cohesive, and let
$\omega $
, let C be cohesive, and let
![]() $\varphi \colon \mathbb {N} \rightarrow |\mathcal {L}|$
be any total computable bijection. Then
$\varphi \colon \mathbb {N} \rightarrow |\mathcal {L}|$
be any total computable bijection. Then
![]() $[\varphi ]$
is not in the image of the canonical embedding of
$[\varphi ]$
is not in the image of the canonical embedding of
![]() $\mathcal {L}$
into
$\mathcal {L}$
into
![]() $\prod _C \mathcal {L}$
, so it must be
$\prod _C \mathcal {L}$
, so it must be
![]() $\prec _{\prod _C \mathcal {L}}$
-above every element in the image of the canonical embedding. Thus
$\prec _{\prod _C \mathcal {L}}$
-above every element in the image of the canonical embedding. Thus
![]() $\prod _C \mathcal {L}$
is of the form
$\prod _C \mathcal {L}$
is of the form
![]() $\omega + \mathcal {M}$
for some non-empty linear order
$\omega + \mathcal {M}$
for some non-empty linear order
![]() $\mathcal {M}$
. By analogy with the terminology for models of arithmetic, we call the elements of the
$\mathcal {M}$
. By analogy with the terminology for models of arithmetic, we call the elements of the
![]() $\omega $
-part of
$\omega $
-part of
![]() $\prod _C \mathcal {L}$
(i.e., the image of the canonical embedding) standard and the elements of the
$\prod _C \mathcal {L}$
(i.e., the image of the canonical embedding) standard and the elements of the
![]() $\mathcal {M}$
-part of
$\mathcal {M}$
-part of
![]() $\prod _C \mathcal {L}$
non-standard. In terms of the finite condensation, we have that
$\prod _C \mathcal {L}$
non-standard. In terms of the finite condensation, we have that
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\prod _C \mathcal {L}) \cong \boldsymbol {1} + \mathcal {N}$
for some linear order
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\prod _C \mathcal {L}) \cong \boldsymbol {1} + \mathcal {N}$
for some linear order
![]() $\mathcal {N}$
. Call the block corresponding to
$\mathcal {N}$
. Call the block corresponding to
![]() $\boldsymbol {1}$
the standard block and the blocks corresponding to
$\boldsymbol {1}$
the standard block and the blocks corresponding to
![]() $\mathcal {N}$
the non-standard blocks. Lemma 4.3 implies that
$\mathcal {N}$
the non-standard blocks. Lemma 4.3 implies that
![]() $\mathcal {N}$
is always infinite and therefore that
$\mathcal {N}$
is always infinite and therefore that
![]() $\mathcal {M}$
is always infinite as well.
$\mathcal {M}$
is always infinite as well.
Lemma 4.2. Let
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
be a computable copy of
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
be a computable copy of
![]() $\omega $
, let C be cohesive, and let
$\omega $
, let C be cohesive, and let
![]() $[\varphi ]$
be an element of
$[\varphi ]$
be an element of
![]() $\prod _C \mathcal {L}$
. Then
$\prod _C \mathcal {L}$
. Then
![]() $[\varphi ]$
is non-standard if and only if
$[\varphi ]$
is non-standard if and only if
![]() $\liminf _{n \in C} \varphi (n) = \infty $
.
$\liminf _{n \in C} \varphi (n) = \infty $
.
Proof If
![]() $[\varphi ]$
is standard, then
$[\varphi ]$
is standard, then
![]() $\varphi $
is eventually constant on C, so
$\varphi $
is eventually constant on C, so
![]() $\liminf _{n \in C} \varphi (n)$
is finite. Conversely, suppose that
$\liminf _{n \in C} \varphi (n)$
is finite. Conversely, suppose that
![]() $\liminf _{n \in C} \varphi (n) = k$
is finite. Then
$\liminf _{n \in C} \varphi (n) = k$
is finite. Then
![]() $(\exists ^\infty n \in C)(\varphi (n) = k)$
. By cohesiveness, it must therefore be that
$(\exists ^\infty n \in C)(\varphi (n) = k)$
. By cohesiveness, it must therefore be that
![]() $(\forall ^\infty n \in C)(\varphi (n) = k)$
. That is,
$(\forall ^\infty n \in C)(\varphi (n) = k)$
. That is,
![]() $\varphi $
is eventually constant on C, so
$\varphi $
is eventually constant on C, so
![]() $[\varphi ]$
is standard.
$[\varphi ]$
is standard.
In Lemma 4.2, the condition
![]() $\liminf _{n \in C} \varphi (n) = \infty $
may be replaced by either
$\liminf _{n \in C} \varphi (n) = \infty $
may be replaced by either
![]() $\lim _{n \in C} \varphi (n) = \infty $
or
$\lim _{n \in C} \varphi (n) = \infty $
or
![]() $\limsup _{n \in C} \varphi (n) = \infty $
because if C is cohesive,
$\limsup _{n \in C} \varphi (n) = \infty $
because if C is cohesive,
![]() $\varphi $
is partial computable, and
$\varphi $
is partial computable, and
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
, then
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
, then
![]() $\liminf _{n \in C} \varphi (n) = \infty $
,
$\liminf _{n \in C} \varphi (n) = \infty $
,
![]() $\lim _{n \in C} \varphi (n) = \infty $
, and
$\lim _{n \in C} \varphi (n) = \infty $
, and
![]() $\limsup _{n \in C} \varphi (n) = \infty $
are all equivalent conditions.
$\limsup _{n \in C} \varphi (n) = \infty $
are all equivalent conditions.
The following Lemma 4.3 says that if
![]() $\mathcal {L}$
is a computable copy of
$\mathcal {L}$
is a computable copy of
![]() $\omega $
and C is cohesive, then
$\omega $
and C is cohesive, then
![]() $\prod _C \mathcal {L}$
has neither a least nor a greatest non-standard block. If
$\prod _C \mathcal {L}$
has neither a least nor a greatest non-standard block. If
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
![]() $1$
-decidable or C is co-c.e., then this can be proved by a saturation argument similar to that given in the proof of Theorem 3.9. Instead, we give a hands-on proof that works for all computable
$1$
-decidable or C is co-c.e., then this can be proved by a saturation argument similar to that given in the proof of Theorem 3.9. Instead, we give a hands-on proof that works for all computable
![]() $\mathcal {L} \cong \omega $
and all cohesive C.
$\mathcal {L} \cong \omega $
and all cohesive C.
Lemma 4.3. Let
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
be a computable copy of
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
be a computable copy of
![]() $\omega $
, let C be cohesive, and let
$\omega $
, let C be cohesive, and let
![]() $[\varphi ]$
be a non-standard element of
$[\varphi ]$
be a non-standard element of
![]() $\prod _C \mathcal {L}$
. Then there are non-standard elements
$\prod _C \mathcal {L}$
. Then there are non-standard elements
![]() $[\psi ^-]$
and
$[\psi ^-]$
and
![]() $[\psi ^+]$
of
$[\psi ^+]$
of
![]() $\prod _C \mathcal {L}$
with
$\prod _C \mathcal {L}$
with
![]() .
.
Proof Let
![]() $(\ell _i : i \in \mathbb {N})$
be a computable enumeration of L. Compute a sequence
$(\ell _i : i \in \mathbb {N})$
be a computable enumeration of L. Compute a sequence
![]() $x_0 \prec _{\mathcal {L}} x_1 \prec _{\mathcal {L}} x_2 \prec _{\mathcal {L}} \cdots $
that is cofinal in
$x_0 \prec _{\mathcal {L}} x_1 \prec _{\mathcal {L}} x_2 \prec _{\mathcal {L}} \cdots $
that is cofinal in
![]() $\mathcal {L}$
by letting
$\mathcal {L}$
by letting
![]() $x_0 = \ell _0$
and by letting each
$x_0 = \ell _0$
and by letting each
![]() $x_{i+1}$
be the
$x_{i+1}$
be the
![]() $<$
-least number with
$<$
-least number with
![]() $\max _{\prec _{\mathcal {L}}}\{x_i, \ell _i\} \prec _{\mathcal {L}} x_{i+1}$
. Such an
$\max _{\prec _{\mathcal {L}}}\{x_i, \ell _i\} \prec _{\mathcal {L}} x_{i+1}$
. Such an
![]() $x_{i+1}$
always exists because
$x_{i+1}$
always exists because
![]() $\mathcal {L}$
has no
$\mathcal {L}$
has no
![]() $\prec _{\mathcal {L}}$
-maximum element.
$\prec _{\mathcal {L}}$
-maximum element.
Consider a non-standard
![]() $[\varphi ] \in |\prod _C \mathcal {L}|$
. Define partial computable functions
$[\varphi ] \in |\prod _C \mathcal {L}|$
. Define partial computable functions
![]() $\psi ^-, \psi ^+ \colon \mathbb {N} \rightarrow L$
by
$\psi ^-, \psi ^+ \colon \mathbb {N} \rightarrow L$
by
 $$ \begin{align*} \psi^-(n) &\simeq \begin{cases} x_i, & \text{if }x_{2i} \preceq_{\mathcal{L}} \varphi(n) \prec_{\mathcal{L}} x_{2i+2},\\ {\uparrow}, & \text{if }\varphi(n){\uparrow}, \end{cases}\\ \psi^+(n) &\simeq \begin{cases} x_{2i}, & \text{if }x_i \preceq_{\mathcal{L}} \varphi(n) \prec_{\mathcal{L}} x_{i+1},\\ {\uparrow}, & \text{if }\varphi(n){\uparrow}. \end{cases} \end{align*} $$
$$ \begin{align*} \psi^-(n) &\simeq \begin{cases} x_i, & \text{if }x_{2i} \preceq_{\mathcal{L}} \varphi(n) \prec_{\mathcal{L}} x_{2i+2},\\ {\uparrow}, & \text{if }\varphi(n){\uparrow}, \end{cases}\\ \psi^+(n) &\simeq \begin{cases} x_{2i}, & \text{if }x_i \preceq_{\mathcal{L}} \varphi(n) \prec_{\mathcal{L}} x_{i+1},\\ {\uparrow}, & \text{if }\varphi(n){\uparrow}. \end{cases} \end{align*} $$
The element
![]() $[\varphi ]$
is non-standard, so
$[\varphi ]$
is non-standard, so
![]() $(\forall i)(\forall ^\infty n \in C)(x_{2i} \preceq _{\mathcal {L}} \varphi (n))$
. Thus
$(\forall i)(\forall ^\infty n \in C)(x_{2i} \preceq _{\mathcal {L}} \varphi (n))$
. Thus
![]() $(\forall i)(\forall ^\infty n \in C)(x_i \preceq _{\mathcal {L}} \psi ^-(n))$
, so
$(\forall i)(\forall ^\infty n \in C)(x_i \preceq _{\mathcal {L}} \psi ^-(n))$
, so
![]() $[\psi ^-]$
is non-standard as well. Moreover, if
$[\psi ^-]$
is non-standard as well. Moreover, if
![]() $x_{2i} \preceq _{\mathcal {L}} \varphi (n) \prec _{\mathcal {L}} x_{2i+2}$
, then
$x_{2i} \preceq _{\mathcal {L}} \varphi (n) \prec _{\mathcal {L}} x_{2i+2}$
, then
![]() $\psi ^-(n) = x_i$
, and therefore
$\psi ^-(n) = x_i$
, and therefore
![]() $|(\psi ^-(n), \varphi (n))_{\mathcal {L}}| \geq i-1$
because
$|(\psi ^-(n), \varphi (n))_{\mathcal {L}}| \geq i-1$
because
![]() $x_{i+1}, \dots , x_{2i-1} \in (\psi ^-(n), \varphi (n))_{\mathcal {L}}$
. Therefore
$x_{i+1}, \dots , x_{2i-1} \in (\psi ^-(n), \varphi (n))_{\mathcal {L}}$
. Therefore
![]() $\limsup _{n \in C}|(\psi ^-(n), \varphi (n))_{\mathcal {L}}| = \infty $
, so
$\limsup _{n \in C}|(\psi ^-(n), \varphi (n))_{\mathcal {L}}| = \infty $
, so
![]() by Lemma 3.8. Similar reasoning shows that
by Lemma 3.8. Similar reasoning shows that
![]() . Thus
. Thus
![]() .
.
If the computable linear order
![]() $\mathcal {L}$
is 1-decidable or the cohesive set C is co-c.e., then between any two blocks there is a third. We therefore have the following theorem.
$\mathcal {L}$
is 1-decidable or the cohesive set C is co-c.e., then between any two blocks there is a third. We therefore have the following theorem.
Theorem 4.4. Let
![]() $\mathcal {L}$
be a computable copy of
$\mathcal {L}$
be a computable copy of
![]() $\omega $
, and let C be a cohesive set. If either
$\omega $
, and let C be a cohesive set. If either
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
![]() $1$
-decidable or C is co-c.e., then
$1$
-decidable or C is co-c.e., then
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\prod _C \mathcal {L})$
has order-type
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\prod _C \mathcal {L})$
has order-type
![]() $\boldsymbol {1} + \eta $
.
$\boldsymbol {1} + \eta $
.
Proof By Lemma 4.1, the standard elements of
![]() $\prod _C \mathcal {L}$
form an initial block. By Theorem 3.9 and Lemma 4.3, the non-standard blocks of
$\prod _C \mathcal {L}$
form an initial block. By Theorem 3.9 and Lemma 4.3, the non-standard blocks of
![]() $\prod _C \mathcal {L}$
form a countable dense linear order without endpoints. Thus
$\prod _C \mathcal {L}$
form a countable dense linear order without endpoints. Thus
![]() $\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\prod _C \mathcal {L}) \cong \boldsymbol {1} + \eta $
.
$\operatorname {{\mathbf {c}_{\mathrm {F}}}}(\prod _C \mathcal {L}) \cong \boldsymbol {1} + \eta $
.
Thinking in terms of blocks, showing that a linear order
![]() $\mathcal {M}$
has type
$\mathcal {M}$
has type
![]() $\omega + \zeta \eta $
amounts to showing that
$\omega + \zeta \eta $
amounts to showing that
![]() $\mathcal {M}$
consists of an initial block of order-type
$\mathcal {M}$
consists of an initial block of order-type
![]() $\omega $
followed by densely (without endpoints) ordered blocks of type
$\omega $
followed by densely (without endpoints) ordered blocks of type
![]() $\zeta $
.
$\zeta $
.
Theorem 4.5. Let
![]() $\mathcal {L}$
be a computable copy of
$\mathcal {L}$
be a computable copy of
![]() $\omega $
that is computably isomorphic to the usual presentation, and let C be cohesive. Then
$\omega $
that is computably isomorphic to the usual presentation, and let C be cohesive. Then
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \zeta \eta $
.
$\omega + \zeta \eta $
.
Proof As explained above, it follows from [Reference Moses19, Section 3] that a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
is computably isomorphic to the usual presentation if and only if
$\omega $
is computably isomorphic to the usual presentation if and only if
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
![]() $1$
-decidable. Thus we show that if
$1$
-decidable. Thus we show that if
![]() $\mathcal {L}$
is a
$\mathcal {L}$
is a
![]() $1$
-decidable copy of
$1$
-decidable copy of
![]() $\omega $
and C is cohesive, then
$\omega $
and C is cohesive, then
![]() $\prod _C \mathcal {L} \cong \omega + \zeta \eta $
.
$\prod _C \mathcal {L} \cong \omega + \zeta \eta $
.
Let
![]() $\mathcal {L}$
be a
$\mathcal {L}$
be a
![]() $1$
-decidable copy of
$1$
-decidable copy of
![]() $\omega $
, and let C be cohesive. By Lemma 4.1 and Theorem 4.4,
$\omega $
, and let C be cohesive. By Lemma 4.1 and Theorem 4.4,
![]() $\prod _C \mathcal {L}$
consists of an initial standard block of order-type
$\prod _C \mathcal {L}$
consists of an initial standard block of order-type
![]() $\omega $
followed by a densely (without endpoints) ordered collection of non-standard blocks. It remains to show that each non-standard block has order-type
$\omega $
followed by a densely (without endpoints) ordered collection of non-standard blocks. It remains to show that each non-standard block has order-type
![]() $\zeta $
. To do this, it suffices to show that every non-standard element of
$\zeta $
. To do this, it suffices to show that every non-standard element of
![]() $\prod _C \mathcal {L}$
has an
$\prod _C \mathcal {L}$
has an
![]() $\prec _{\prod _C \mathcal {L}}$
-immediate successor and an
$\prec _{\prod _C \mathcal {L}}$
-immediate successor and an
![]() $\prec _{\prod _C \mathcal {L}}$
-immediate predecessor.
$\prec _{\prod _C \mathcal {L}}$
-immediate predecessor.
Let
![]() $[\varphi ] \in |\prod _C \mathcal {L}|$
. As
$[\varphi ] \in |\prod _C \mathcal {L}|$
. As
![]() $\mathcal {L} \cong \omega $
, we have that
$\mathcal {L} \cong \omega $
, we have that
The linear order
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
![]() $1$
-decidable and the relevant formula is
$1$
-decidable and the relevant formula is
![]() $\Sigma _2$
, so
$\Sigma _2$
, so
![]() $[\varphi ]$
has a
$[\varphi ]$
has a
![]() $\prec _{\prod _C \mathcal {L}}$
-immediate successor in
$\prec _{\prod _C \mathcal {L}}$
-immediate successor in
![]() $\prod _C \mathcal {L}$
by the
$\prod _C \mathcal {L}$
by the
![]() $n=1$
case of Theorem 2.9 item (1). Now additionally suppose that
$n=1$
case of Theorem 2.9 item (1). Now additionally suppose that
![]() $[\varphi ]$
is not the
$[\varphi ]$
is not the
![]() $\prec _{\prod _C \mathcal {L}}$
-least element of
$\prec _{\prod _C \mathcal {L}}$
-least element of
![]() $\prod _C \mathcal {L}$
. Then for almost every
$\prod _C \mathcal {L}$
. Then for almost every
![]() $n \in C$
,
$n \in C$
,
![]() $\varphi (n)$
is not the
$\varphi (n)$
is not the
![]() $\prec _{\mathcal {L}}$
-least element of
$\prec _{\mathcal {L}}$
-least element of
![]() $\mathcal {L}$
. Therefore
$\mathcal {L}$
. Therefore
so
![]() $[\varphi ]$
has an
$[\varphi ]$
has an
![]() $\prec _{\prod _C \mathcal {L}}$
-immediate predecessor in
$\prec _{\prod _C \mathcal {L}}$
-immediate predecessor in
![]() $\prod _C \mathcal {L}$
by Theorem 2.9 item (1). It follows that if
$\prod _C \mathcal {L}$
by Theorem 2.9 item (1). It follows that if
![]() $[\varphi ]$
is non-standard, then it has both an
$[\varphi ]$
is non-standard, then it has both an
![]() $\prec _{\prod _C \mathcal {L}}$
-immediate successor and an
$\prec _{\prod _C \mathcal {L}}$
-immediate successor and an
![]() $\prec _{\prod _C \mathcal {L}}$
-immediate predecessor in
$\prec _{\prod _C \mathcal {L}}$
-immediate predecessor in
![]() $\prod _C \mathcal {L}$
, which completes the proof.
$\prod _C \mathcal {L}$
, which completes the proof.
We can calculate the order-types of the cohesive powers of many other computable presentations of linear orders by combining Theorems 2.20, 3.6, 4.5, and the fact that
![]() $\prod _C \mathbb {Q} \cong \eta $
.
$\prod _C \mathbb {Q} \cong \eta $
.
Example 4.6. Let C be a cohesive set. Let
![]() $\mathbb {N}$
,
$\mathbb {N}$
,
![]() $\mathbb {Z}$
, and
$\mathbb {Z}$
, and
![]() $\mathbb {Q}$
denote the usual presentations of
$\mathbb {Q}$
denote the usual presentations of
![]() $\omega $
,
$\omega $
,
![]() $\zeta $
, and
$\zeta $
, and
![]() $\eta $
.
$\eta $
.
-
(1)
 $\prod _C \mathbb {N}^* \cong \zeta \eta + \omega ^*$
. This is because
$\prod _C \mathbb {N}^* \cong \zeta \eta + \omega ^*$
. This is because  $$ \begin{align*} \prod\nolimits_C \mathbb{N}^* \;\cong\; \left(\prod\nolimits_C \mathbb{N}\right)^* \;\cong\; (\omega + \zeta\eta)^* \;\cong\; \zeta\eta + \omega^*. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathbb{N}^* \;\cong\; \left(\prod\nolimits_C \mathbb{N}\right)^* \;\cong\; (\omega + \zeta\eta)^* \;\cong\; \zeta\eta + \omega^*. \end{align*} $$
-
(2)
 $\prod _C \mathbb {Z} \cong \zeta \eta $
. This is because
$\prod _C \mathbb {Z} \cong \zeta \eta $
. This is because
 $\mathbb {Z}$
is computably isomorphic to
$\mathbb {Z}$
is computably isomorphic to
 $\mathbb {N}^* + \mathbb {N}$
, so
$\mathbb {N}^* + \mathbb {N}$
, so  $$ \begin{align*} \prod\nolimits_C \mathbb{Z} \;&\cong\; \prod\nolimits_C(\mathbb{N}^* + \mathbb{N}) \;\cong\; \prod\nolimits_C \mathbb{N}^* + \prod\nolimits_C \mathbb{N} \\ & \cong\; (\zeta\eta + \omega^*) + (\omega + \zeta\eta) \;\cong\; \zeta\eta + \zeta + \zeta\eta \;\cong\; \zeta\eta. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathbb{Z} \;&\cong\; \prod\nolimits_C(\mathbb{N}^* + \mathbb{N}) \;\cong\; \prod\nolimits_C \mathbb{N}^* + \prod\nolimits_C \mathbb{N} \\ & \cong\; (\zeta\eta + \omega^*) + (\omega + \zeta\eta) \;\cong\; \zeta\eta + \zeta + \zeta\eta \;\cong\; \zeta\eta. \end{align*} $$
-
(3)
 $\prod _C(\mathbb {Z}\mathbb {Q}) \cong \zeta \eta $
. This is because
$\prod _C(\mathbb {Z}\mathbb {Q}) \cong \zeta \eta $
. This is because  $$ \begin{align*} \prod\nolimits_C(\mathbb{Z}\mathbb{Q}) \;\cong\; \left( \prod\nolimits_C \mathbb{Z} \right) \left( \prod\nolimits_C\mathbb{Q} \right) \;\cong\; (\zeta\eta)\eta \;\cong\; \zeta\eta. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C(\mathbb{Z}\mathbb{Q}) \;\cong\; \left( \prod\nolimits_C \mathbb{Z} \right) \left( \prod\nolimits_C\mathbb{Q} \right) \;\cong\; (\zeta\eta)\eta \;\cong\; \zeta\eta. \end{align*} $$
-
(4)
 $\prod _C(\mathbb {N} + \mathbb {Z}\mathbb {Q}) \cong \omega + \zeta \eta $
. This is because
$\prod _C(\mathbb {N} + \mathbb {Z}\mathbb {Q}) \cong \omega + \zeta \eta $
. This is because  $$ \begin{align*} \prod\nolimits_C(\mathbb{N} + \mathbb{Z}\mathbb{Q}) \;\cong\; \prod\nolimits_C \mathbb{N} + \prod\nolimits_C(\mathbb{Z}\mathbb{Q}) \;\cong\; (\omega + \zeta\eta) + \zeta\eta \;\cong\; \omega + \zeta\eta. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C(\mathbb{N} + \mathbb{Z}\mathbb{Q}) \;\cong\; \prod\nolimits_C \mathbb{N} + \prod\nolimits_C(\mathbb{Z}\mathbb{Q}) \;\cong\; (\omega + \zeta\eta) + \zeta\eta \;\cong\; \omega + \zeta\eta. \end{align*} $$
Recall that, by Proposition 3.4, an ultrahomogeneous computable structure for a finite relational language, like the computable linear order
![]() $\mathbb {Q}$
, is isomorphic to each of its cohesive powers. Notice, however, that the computable linear orders
$\mathbb {Q}$
, is isomorphic to each of its cohesive powers. Notice, however, that the computable linear orders
![]() $\mathbb {Z}\mathbb {Q}$
and
$\mathbb {Z}\mathbb {Q}$
and
![]() $\mathbb {N} + \mathbb {Z}\mathbb {Q}$
are not ultrahomogeneous, yet nevertheless are isomorphic to each of their respective cohesive powers. Thus it is also possible for a non-ultrahomogeneous computable structure to be isomorphic to each of its cohesive powers.
$\mathbb {N} + \mathbb {Z}\mathbb {Q}$
are not ultrahomogeneous, yet nevertheless are isomorphic to each of their respective cohesive powers. Thus it is also possible for a non-ultrahomogeneous computable structure to be isomorphic to each of its cohesive powers.
Notice also that
![]() $\prod _C \mathbb {N}$
and
$\prod _C \mathbb {N}$
and
![]() $\prod _C(\mathbb {N} + \mathbb {Z}\mathbb {Q})$
both have order-type
$\prod _C(\mathbb {N} + \mathbb {Z}\mathbb {Q})$
both have order-type
![]() $\omega + \zeta \eta $
. Similarly,
$\omega + \zeta \eta $
. Similarly,
![]() $\prod _C \mathbb {Z}$
and
$\prod _C \mathbb {Z}$
and
![]() $\prod _C(\mathbb {Z}\mathbb {Q})$
both have order-type
$\prod _C(\mathbb {Z}\mathbb {Q})$
both have order-type
![]() $\zeta \eta $
. Thus it is possible for non-isomorphic linear orders to have isomorphic cohesive powers. In Section 5, we give an example of a pair of non-elementarily equivalent linear orders with isomorphic cohesive powers.
$\zeta \eta $
. Thus it is possible for non-isomorphic linear orders to have isomorphic cohesive powers. In Section 5, we give an example of a pair of non-elementarily equivalent linear orders with isomorphic cohesive powers.
Now we give an example of a computable copy of
![]() $\omega $
that is not computably isomorphic to the usual presentation, yet still has all its cohesive powers isomorphic to
$\omega $
that is not computably isomorphic to the usual presentation, yet still has all its cohesive powers isomorphic to
![]() $\omega + \zeta \eta $
.
$\omega + \zeta \eta $
.
Theorem 4.7. There is a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
such that
$\omega $
such that
![]() $:$
$:$
-
•
 $\mathcal {L}$
is not computably isomorphic to the usual presentation of
$\mathcal {L}$
is not computably isomorphic to the usual presentation of
 $\omega $
, yet
$\omega $
, yet -
• for every cohesive set C, the cohesive power
 $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
 $\omega + \zeta \eta $
.
$\omega + \zeta \eta $
.
Proof We use a classic example of a computable copy of
![]() $\omega $
with a non-computable immediate successor relation. Fix any non-computable c.e. set A, and let
$\omega $
with a non-computable immediate successor relation. Fix any non-computable c.e. set A, and let
![]() $f \colon \mathbb {N} \rightarrow A$
be a computable bijection. Let
$f \colon \mathbb {N} \rightarrow A$
be a computable bijection. Let
![]() $\mathcal {L} =(\mathbb {N} ,\prec _{\mathcal {L}})$
be the linear order obtained by ordering the even numbers according to their usual order and by setting
$\mathcal {L} =(\mathbb {N} ,\prec _{\mathcal {L}})$
be the linear order obtained by ordering the even numbers according to their usual order and by setting
![]() $2a \prec _{\mathcal {L}} 2k + 1 \prec _{\mathcal {L}} 2a + 2$
if and only if
$2a \prec _{\mathcal {L}} 2k + 1 \prec _{\mathcal {L}} 2a + 2$
if and only if
![]() $f(k) = a$
. Specifically, define:
$f(k) = a$
. Specifically, define:
 $$ \begin{align*} 2c &\prec_{\mathcal{L}} 2d & &\Leftrightarrow & 2c &< 2d, \\ 2c &\prec_{\mathcal{L}} 2k + 1 & &\Leftrightarrow & c &\leq f(k), \\ 2k + 1 &\prec_{\mathcal{L}} 2c & &\Leftrightarrow & f(k) &< c, \\ 2k + 1 &\prec_{\mathcal{L}} 2\ell + 1 & &\Leftrightarrow & f(k) &< f(\ell). \end{align*} $$
$$ \begin{align*} 2c &\prec_{\mathcal{L}} 2d & &\Leftrightarrow & 2c &< 2d, \\ 2c &\prec_{\mathcal{L}} 2k + 1 & &\Leftrightarrow & c &\leq f(k), \\ 2k + 1 &\prec_{\mathcal{L}} 2c & &\Leftrightarrow & f(k) &< c, \\ 2k + 1 &\prec_{\mathcal{L}} 2\ell + 1 & &\Leftrightarrow & f(k) &< f(\ell). \end{align*} $$
Then
![]() $\mathcal {L}$
is a computable linear order of type
$\mathcal {L}$
is a computable linear order of type
![]() $\omega $
. Let
$\omega $
. Let
![]() $S^{\mathcal {L}}$
denote the immediate successor relation of
$S^{\mathcal {L}}$
denote the immediate successor relation of
![]() $\mathcal {L}$
. Then
$\mathcal {L}$
. Then
![]() $A \leq _{\mathrm {T}} S^{\mathcal {L}}$
(in fact,
$A \leq _{\mathrm {T}} S^{\mathcal {L}}$
(in fact,
![]() $A \equiv _{\mathrm {T}} S^{\mathcal {L}}$
) because
$A \equiv _{\mathrm {T}} S^{\mathcal {L}}$
) because
![]() $a \in A$
if and only if
$a \in A$
if and only if
![]() $\neg S^{\mathcal {L}}(2a, 2a+2)$
. Thus
$\neg S^{\mathcal {L}}(2a, 2a+2)$
. Thus
![]() $S^{\mathcal {L}}$
is not computable, so
$S^{\mathcal {L}}$
is not computable, so
![]() $\mathcal {L}$
is not computably isomorphic to the usual presentation of
$\mathcal {L}$
is not computably isomorphic to the usual presentation of
![]() $\omega $
.
$\omega $
.
Let C be cohesive. We show that
![]() $\prod _C \mathcal {L} \cong \omega + \zeta \eta $
. To do this, expand the language to
$\prod _C \mathcal {L} \cong \omega + \zeta \eta $
. To do this, expand the language to
![]() $\{\prec , E, R\}$
, where E is a unary relation symbol and R is a binary relation symbol. Expand
$\{\prec , E, R\}$
, where E is a unary relation symbol and R is a binary relation symbol. Expand
![]() $\mathcal {L}$
by interpreting E as the evens and by interpreting R as the immediate successor relation among the evens:
$\mathcal {L}$
by interpreting E as the evens and by interpreting R as the immediate successor relation among the evens:
 $$ \begin{align*} E^{\mathcal{L}}(a) \quad&\Leftrightarrow\quad a = 2n\text{ for some }n,\\ R^{\mathcal{L}}(a, b) \quad&\Leftrightarrow\quad a = 2n\text{ and }b = 2n+2\text{ for some }n. \end{align*} $$
$$ \begin{align*} E^{\mathcal{L}}(a) \quad&\Leftrightarrow\quad a = 2n\text{ for some }n,\\ R^{\mathcal{L}}(a, b) \quad&\Leftrightarrow\quad a = 2n\text{ and }b = 2n+2\text{ for some }n. \end{align*} $$
Now consider the substructure
![]() $\mathcal {B}$
of
$\mathcal {B}$
of
![]() $\mathcal {L}$
with domain
$\mathcal {L}$
with domain
![]() $\{a \in |\mathcal {L}| : E^{\mathcal {L}}(a)\}$
and the substructure
$\{a \in |\mathcal {L}| : E^{\mathcal {L}}(a)\}$
and the substructure
![]() $\mathcal {D}$
of
$\mathcal {D}$
of
![]() $\prod _C \mathcal {L}$
with domain
$\prod _C \mathcal {L}$
with domain
![]() $\bigl \{[\varphi ] \in |\prod _C \mathcal {L}| : E^{\prod _C \mathcal {L}}([\varphi ])\bigr \}$
. As a linear order,
$\bigl \{[\varphi ] \in |\prod _C \mathcal {L}| : E^{\prod _C \mathcal {L}}([\varphi ])\bigr \}$
. As a linear order,
![]() $\mathcal {B}$
is computably isomorphic to the usual presentation of
$\mathcal {B}$
is computably isomorphic to the usual presentation of
![]() $\omega $
. Therefore
$\omega $
. Therefore
![]() $\mathcal {D} \cong \prod _C \mathcal {B} \cong \omega + \zeta \eta $
as linear orders by Proposition 2.12 and Theorem 4.5.
$\mathcal {D} \cong \prod _C \mathcal {B} \cong \omega + \zeta \eta $
as linear orders by Proposition 2.12 and Theorem 4.5.
In
![]() $\mathcal {L}$
, if z is not in the substructure
$\mathcal {L}$
, if z is not in the substructure
![]() $\mathcal {B}$
, then z is the unique element
$\mathcal {B}$
, then z is the unique element
![]() $\prec _{\mathcal {L}}$
-between two consecutive elements of
$\prec _{\mathcal {L}}$
-between two consecutive elements of
![]() $\mathcal {B}$
. That is,
$\mathcal {B}$
. That is,
![]() $\mathcal {L}$
satisfies the following
$\mathcal {L}$
satisfies the following
![]() $\Pi _2$
sentences:
$\Pi _2$
sentences:
 $$ \begin{align*} \mathcal{L} &\models \forall z \, [\neg E(z) \;\rightarrow\; \exists x \exists y \, (R(x,y) \,\wedge\, x \prec z \prec y)],\\ \mathcal{L} &\models \forall x \forall y \forall z_0 \forall z_1 \, [(R(x,y) \,\wedge\, x \prec z_0 \prec y \,\wedge\, x \prec z_1 \prec y) \;\rightarrow\; z_0 = z_1]. \end{align*} $$
$$ \begin{align*} \mathcal{L} &\models \forall z \, [\neg E(z) \;\rightarrow\; \exists x \exists y \, (R(x,y) \,\wedge\, x \prec z \prec y)],\\ \mathcal{L} &\models \forall x \forall y \forall z_0 \forall z_1 \, [(R(x,y) \,\wedge\, x \prec z_0 \prec y \,\wedge\, x \prec z_1 \prec y) \;\rightarrow\; z_0 = z_1]. \end{align*} $$
By Theorem 2.9 item (2),
![]() $\prod _C \mathcal {L}$
also satisfies these sentences. Thus in
$\prod _C \mathcal {L}$
also satisfies these sentences. Thus in
![]() $\prod _C \mathcal {L}$
, if some
$\prod _C \mathcal {L}$
, if some
![]() $[\varphi ]$
is not in the substructure
$[\varphi ]$
is not in the substructure
![]() $\mathcal {D}$
, then
$\mathcal {D}$
, then
![]() $[\varphi ]$
is the unique element
$[\varphi ]$
is the unique element
![]() $\prec _{\prod _C \mathcal {L}}$
-between two consecutive elements of
$\prec _{\prod _C \mathcal {L}}$
-between two consecutive elements of
![]() $\mathcal {D}$
. As
$\mathcal {D}$
. As
![]() $\mathcal {D} \cong \omega + \zeta \eta $
, we may conclude that
$\mathcal {D} \cong \omega + \zeta \eta $
, we may conclude that
![]() $\prod _C \mathcal {L} \cong \omega + \zeta \eta $
as well.
$\prod _C \mathcal {L} \cong \omega + \zeta \eta $
as well.
Now we show that for every cohesive set C, there is a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
such that
$\omega $
such that
![]() $\prod _C \mathcal {L}$
is not isomorphic, indeed, not elementarily equivalent, to
$\prod _C \mathcal {L}$
is not isomorphic, indeed, not elementarily equivalent, to
![]() $\omega + \zeta \eta $
. The strategy is to arrange for the element
$\omega + \zeta \eta $
. The strategy is to arrange for the element
![]() $[\operatorname {{\mathrm {id}}}]$
of
$[\operatorname {{\mathrm {id}}}]$
of
![]() $\prod _C \mathcal {L}$
represented by the identity function
$\prod _C \mathcal {L}$
represented by the identity function
![]() $\operatorname {{\mathrm {id}}} \colon \mathbb {N} \rightarrow \mathbb {N}$
to have no
$\operatorname {{\mathrm {id}}} \colon \mathbb {N} \rightarrow \mathbb {N}$
to have no
![]() $\prec _{\prod _C \mathcal {L}}$
-immediate successor. This exhibits an elementary difference between
$\prec _{\prod _C \mathcal {L}}$
-immediate successor. This exhibits an elementary difference between
![]() $\prod _C \mathcal {L}$
and
$\prod _C \mathcal {L}$
and
![]() $\omega + \zeta \eta $
because every element of
$\omega + \zeta \eta $
because every element of
![]() $\omega + \zeta \eta $
has an immediate successor. This also shows that Theorem 2.9 item (3) is tight: “every element has an immediate successor” is a
$\omega + \zeta \eta $
has an immediate successor. This also shows that Theorem 2.9 item (3) is tight: “every element has an immediate successor” is a
![]() $\Pi _3$
sentence that is true of
$\Pi _3$
sentence that is true of
![]() $\mathcal {L}$
but not of
$\mathcal {L}$
but not of
![]() $\prod _C \mathcal {L}$
.
$\prod _C \mathcal {L}$
.
Theorem 4.8. Let C be any cohesive set. Then there is a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
for which
$\omega $
for which
![]() $\prod _C \mathcal {L}$
is not elementarily equivalent (and hence not isomorphic) to
$\prod _C \mathcal {L}$
is not elementarily equivalent (and hence not isomorphic) to
![]() $\omega + \zeta \eta $
.
$\omega + \zeta \eta $
.
Proof Let
![]() $(\varphi _e)_{e \in \mathbb {N}}$
denote the usual effective list of all partial computable functions, and recall that
$(\varphi _e)_{e \in \mathbb {N}}$
denote the usual effective list of all partial computable functions, and recall that
![]() $\varphi _{e,s}(n)$
denotes the result of running
$\varphi _{e,s}(n)$
denotes the result of running
![]() $\varphi _e$
on input n for s computational steps. We compute a linear order
$\varphi _e$
on input n for s computational steps. We compute a linear order
![]() $\mathcal {L} = (\mathbb {N}, \prec _{\mathcal {L}})$
of type
$\mathcal {L} = (\mathbb {N}, \prec _{\mathcal {L}})$
of type
![]() $\omega $
such that for every
$\omega $
such that for every
![]() $\varphi _e$
:
$\varphi _e$
:
By Lemma 3.7, achieving (*) for
![]() $\varphi _e$
ensures that
$\varphi _e$
ensures that
![]() $[\varphi _e]$
is not the
$[\varphi _e]$
is not the
![]() $\prec _{\prod _C \mathcal {L}}$
-immediate successor of
$\prec _{\prod _C \mathcal {L}}$
-immediate successor of
![]() $[\operatorname {{\mathrm {id}}}]$
in
$[\operatorname {{\mathrm {id}}}]$
in
![]() $\prod _C \mathcal {L}$
. Therefore, achieving (*) for every
$\prod _C \mathcal {L}$
. Therefore, achieving (*) for every
![]() $\varphi _e$
ensures that
$\varphi _e$
ensures that
![]() $[\operatorname {{\mathrm {id}}}]$
has no
$[\operatorname {{\mathrm {id}}}]$
has no
![]() $\prec _{\prod _C \mathcal {L}}$
-immediate successor in
$\prec _{\prod _C \mathcal {L}}$
-immediate successor in
![]() $\prod _C \mathcal {L}$
. Thus
$\prod _C \mathcal {L}$
. Thus
![]() $\prod _C \mathcal {L}$
is not elementarily equivalent to
$\prod _C \mathcal {L}$
is not elementarily equivalent to
![]() $\omega + \zeta \eta $
because every element of
$\omega + \zeta \eta $
because every element of
![]() $\omega + \zeta \eta $
has an immediate successor, which is a
$\omega + \zeta \eta $
has an immediate successor, which is a
![]() $\Pi _3$
property.
$\Pi _3$
property.
Fix an infinite computable set
![]() $R \subseteq \overline {C}$
. Such an R may be obtained, for example, by partitioning
$R \subseteq \overline {C}$
. Such an R may be obtained, for example, by partitioning
![]() $\mathbb {N}$
into the even numbers
$\mathbb {N}$
into the even numbers
![]() $R_0$
and the odd numbers
$R_0$
and the odd numbers
![]() $R_1$
. By cohesiveness,
$R_1$
. By cohesiveness,
![]() $C \subseteq ^* R_i$
for either
$C \subseteq ^* R_i$
for either
![]() $i = 0$
or
$i = 0$
or
![]() $i = 1$
, in which case
$i = 1$
, in which case
![]() $R_{1-i} \subseteq ^* \overline {C}$
. Thus we may take R to be an appropriate tail of
$R_{1-i} \subseteq ^* \overline {C}$
. Thus we may take R to be an appropriate tail of
![]() $R_{1-i}$
.
$R_{1-i}$
.
Define
![]() $\prec _{\mathcal {L}}$
in stages. By the end of stage s,
$\prec _{\mathcal {L}}$
in stages. By the end of stage s,
![]() $\prec _{\mathcal {L}}$
will have been defined on
$\prec _{\mathcal {L}}$
will have been defined on
![]() $X_s \times X_s$
for some finite
$X_s \times X_s$
for some finite
![]() $X_s \supseteq \{0,1,\dots , s\}$
. As the construction progresses, at some stage we may notice an e and n such that
$X_s \supseteq \{0,1,\dots , s\}$
. As the construction progresses, at some stage we may notice an e and n such that
![]() $\varphi _e(n) = a$
looks like the
$\varphi _e(n) = a$
looks like the
![]() $\prec _{\mathcal {L}}$
-immediate successor of n, where n may or may not be in C. In this case, we want to add an m to the order and set
$\prec _{\mathcal {L}}$
-immediate successor of n, where n may or may not be in C. In this case, we want to add an m to the order and set
![]() $n \prec _{\mathcal {L}} m \prec _{\mathcal {L}} a$
to help achieve (*) for
$n \prec _{\mathcal {L}} m \prec _{\mathcal {L}} a$
to help achieve (*) for
![]() $\varphi _e$
. If we choose an m that may be in C, then at some later stage there may be an i for which
$\varphi _e$
. If we choose an m that may be in C, then at some later stage there may be an i for which
![]() $\varphi _i(m) = a$
looks like the
$\varphi _i(m) = a$
looks like the
![]() $\prec _{\mathcal {L}}$
-immediate successor of m, and then we would want to add another element
$\prec _{\mathcal {L}}$
-immediate successor of m, and then we would want to add another element
![]() $\prec _{\mathcal {L}}$
-below a. If this happens infinitely often, then we would add infinitely many elements
$\prec _{\mathcal {L}}$
-below a. If this happens infinitely often, then we would add infinitely many elements
![]() $\prec _{\mathcal {L}}$
-below a, in which case
$\prec _{\mathcal {L}}$
-below a, in which case
![]() $\mathcal {L}$
would not be a copy of
$\mathcal {L}$
would not be a copy of
![]() $\omega $
. We avoid this problem by choosing m from R, which is safe because
$\omega $
. We avoid this problem by choosing m from R, which is safe because
![]() $R \subseteq \overline {C}$
. Since we know that
$R \subseteq \overline {C}$
. Since we know that
![]() $m \notin C$
, we do not need to worry about it when trying to achieve (*).
$m \notin C$
, we do not need to worry about it when trying to achieve (*).
At stage
![]() $0$
, set
$0$
, set
![]() $X_0 = \{0\}$
and define
$X_0 = \{0\}$
and define
![]() $0 \nprec _{\mathcal {L}} 0$
. At stage
$0 \nprec _{\mathcal {L}} 0$
. At stage
![]() $s> 0$
, start with
$s> 0$
, start with
![]() $X_s = X_{s-1}$
, and update
$X_s = X_{s-1}$
, and update
![]() $X_s$
and
$X_s$
and
![]() $\prec _{\mathcal {L}}$
according to the following procedure.
$\prec _{\mathcal {L}}$
according to the following procedure.
-
(1) If
 $\prec _{\mathcal {L}}$
has not yet been defined on s (i.e., if
$\prec _{\mathcal {L}}$
has not yet been defined on s (i.e., if
 $s \notin X_s$
), then update
$s \notin X_s$
), then update
 $X_s$
to
$X_s$
to
 $X_s \cup \{s\}$
and extend
$X_s \cup \{s\}$
and extend
 $\prec _{\mathcal {L}}$
to make s the
$\prec _{\mathcal {L}}$
to make s the
 $\prec _{\mathcal {L}}$
-greatest element of
$\prec _{\mathcal {L}}$
-greatest element of
 $X_s$
.
$X_s$
. -
(2) Consider each
 $\langle e, n \rangle < s$
in order. For each
$\langle e, n \rangle < s$
in order. For each
 $\langle e,n \rangle < s$
, if:
$\langle e,n \rangle < s$
, if:-
(a)
 $\varphi _{e,s}(n){\downarrow } \in X_s$
,
$\varphi _{e,s}(n){\downarrow } \in X_s$
, -
(b)
 $\varphi _e(n)$
is currently the
$\varphi _e(n)$
is currently the
 $\prec _{\mathcal {L}}$
-immediate successor of n in
$\prec _{\mathcal {L}}$
-immediate successor of n in
 $X_s$
,
$X_s$
, -
(c)
 $n \notin R$
, and
$n \notin R$
, and -
(d) n is not
 $\preceq _{\mathcal {L}}$
-below any of
$\preceq _{\mathcal {L}}$
-below any of
 $0, 1, \dots , e$
,
$0, 1, \dots , e$
,
then let m be the
 $<$
-least element of
$<$
-least element of
 $R \setminus X_s$
, update
$R \setminus X_s$
, update
 $X_s$
to
$X_s$
to
 $X_s \cup \{m\}$
, and extend
$X_s \cup \{m\}$
, and extend
 $\prec _{\mathcal {L}}$
so that
$\prec _{\mathcal {L}}$
so that
 $n \prec _{\mathcal {L}} m \prec _{\mathcal {L}} \varphi _e(n)$
.
$n \prec _{\mathcal {L}} m \prec _{\mathcal {L}} \varphi _e(n)$
. -
This completes the construction.
We claim that for every k, there are only finitely many elements
![]() $\prec _{\mathcal {L}}$
-below k. It follows that
$\prec _{\mathcal {L}}$
-below k. It follows that
![]() $\mathcal {L}$
has order-type
$\mathcal {L}$
has order-type
![]() $\omega $
. Say that
$\omega $
. Say that
![]() $\varphi _e$
acts for n and adds m when
$\varphi _e$
acts for n and adds m when
![]() $\prec _{\mathcal {L}}$
is defined on an
$\prec _{\mathcal {L}}$
is defined on an
![]() $m \in R$
to make
$m \in R$
to make
![]() $n \prec _{\mathcal {L}} m \prec _{\mathcal {L}} \varphi _e(n)$
as in (2). Let
$n \prec _{\mathcal {L}} m \prec _{\mathcal {L}} \varphi _e(n)$
as in (2). Let
![]() $s_0$
be a stage with
$s_0$
be a stage with
![]() $k \in X_{s_0}$
. Suppose at some stage
$k \in X_{s_0}$
. Suppose at some stage
![]() $s> s_0$
, an m is added to
$s> s_0$
, an m is added to
![]() $X_s$
and
$X_s$
and
![]() $m \prec _{\mathcal {L}} k$
is defined. This can only be due to a
$m \prec _{\mathcal {L}} k$
is defined. This can only be due to a
![]() $\varphi _e$
acting for an
$\varphi _e$
acting for an
![]() $n \notin R$
and adding m at stage s. Thus at stage s, it must be that
$n \notin R$
and adding m at stage s. Thus at stage s, it must be that
![]() $n \prec _{\mathcal {L}} k$
because
$n \prec _{\mathcal {L}} k$
because
![]() $n \prec _{\mathcal {L}} m \prec _{\mathcal {L}} k$
. Therefore it must also be that
$n \prec _{\mathcal {L}} m \prec _{\mathcal {L}} k$
. Therefore it must also be that
![]() $e < k$
, for otherwise k would be among
$e < k$
, for otherwise k would be among
![]() $0,1,\dots , e$
, and condition (d) would prevent the action of
$0,1,\dots , e$
, and condition (d) would prevent the action of
![]() $\varphi _e$
. Furthermore, m is chosen from R, so only elements of R are added
$\varphi _e$
. Furthermore, m is chosen from R, so only elements of R are added
![]() $\prec _{\mathcal {L}}$
-below k after stage
$\prec _{\mathcal {L}}$
-below k after stage
![]() $s_0$
. All together, this means that an m can only be added
$s_0$
. All together, this means that an m can only be added
![]() $\prec _{\mathcal {L}}$
-below k after stage
$\prec _{\mathcal {L}}$
-below k after stage
![]() $s_0$
when a
$s_0$
when a
![]() $\varphi _e$
with
$\varphi _e$
with
![]() $e < k$
acts for an
$e < k$
acts for an
![]() $n \prec _{\mathcal {L}} k$
with
$n \prec _{\mathcal {L}} k$
with
![]() $n \notin R$
. Each
$n \notin R$
. Each
![]() $\varphi _e$
acts at most once for each n, and no new
$\varphi _e$
acts at most once for each n, and no new
![]() $n \notin R$
appears
$n \notin R$
appears
![]() $\prec _{\mathcal {L}}$
-below k after stage
$\prec _{\mathcal {L}}$
-below k after stage
![]() $s_0$
. Thus after stage
$s_0$
. Thus after stage
![]() $s_0$
, only finitely many m are ever added
$s_0$
, only finitely many m are ever added
![]() $\prec _{\mathcal {L}}$
-below k.
$\prec _{\mathcal {L}}$
-below k.
Finally, we claim that (*) is satisfied for every
![]() $\varphi _e$
. Given e, let
$\varphi _e$
. Given e, let
![]() $\ell $
be the
$\ell $
be the
![]() $\prec _{\mathcal {L}}$
-maximum element of
$\prec _{\mathcal {L}}$
-maximum element of
![]() $\{0, 1, \dots , e\}$
. Observe that almost every
$\{0, 1, \dots , e\}$
. Observe that almost every
![]() $n \in \mathbb {N}$
satisfies
$n \in \mathbb {N}$
satisfies
![]() $n \succ _{\mathcal {L}} \ell $
because
$n \succ _{\mathcal {L}} \ell $
because
![]() $\mathcal {L} \cong \omega $
. So suppose that
$\mathcal {L} \cong \omega $
. So suppose that
![]() $n \succ _{\mathcal {L}} \ell $
and
$n \succ _{\mathcal {L}} \ell $
and
![]() $n \in C$
. If
$n \in C$
. If
![]() $\varphi _e(n){\downarrow }$
, let s be large enough so that
$\varphi _e(n){\downarrow }$
, let s be large enough so that
![]() $\langle e, n \rangle < s$
,
$\langle e, n \rangle < s$
,
![]() $\varphi _{e,s}(n){\downarrow }$
,
$\varphi _{e,s}(n){\downarrow }$
,
![]() $n \in X_s$
, and
$n \in X_s$
, and
![]() $\varphi _e(n) \in X_s$
. Then either
$\varphi _e(n) \in X_s$
. Then either
![]() $\varphi _e(n)$
is already not the
$\varphi _e(n)$
is already not the
![]() $\prec _{\mathcal {L}}$
-immediate successor of n at stage
$\prec _{\mathcal {L}}$
-immediate successor of n at stage
![]() $s+1$
, or at stage
$s+1$
, or at stage
![]() $s+1$
the conditions of (2) are satisfied for
$s+1$
the conditions of (2) are satisfied for
![]() $\langle e, n \rangle $
, and an m is added such that
$\langle e, n \rangle $
, and an m is added such that
![]() $n \prec _{\mathcal {L}} m \prec _{\mathcal {L}} \varphi _e(n)$
. This completes the proof.
$n \prec _{\mathcal {L}} m \prec _{\mathcal {L}} \varphi _e(n)$
. This completes the proof.
Corollary 4.9. Theorem 2.9 item (3) cannot be improved in general: there is a computable linear order
![]() $\mathcal {L}$
, a cohesive set C, and a
$\mathcal {L}$
, a cohesive set C, and a
![]() $\Pi _3$
sentence
$\Pi _3$
sentence
![]() $\Phi $
such that
$\Phi $
such that
![]() $\mathcal {L} \models \Phi $
, but
$\mathcal {L} \models \Phi $
, but
![]() $\prod _C \mathcal {L} \not \models \Phi $
.
$\prod _C \mathcal {L} \not \models \Phi $
.
Proof Let C be any cohesive set, and let
![]() $\mathcal {L}$
be a computable copy of
$\mathcal {L}$
be a computable copy of
![]() $\omega $
as in Theorem 4.8 for C. Let
$\omega $
as in Theorem 4.8 for C. Let
![]() $\Phi $
be a
$\Phi $
be a
![]() $\Pi _3$
sentence in the language of linear orders expressing that every element has an immediate successor. Then
$\Pi _3$
sentence in the language of linear orders expressing that every element has an immediate successor. Then
![]() $\mathcal {L} \models \Phi $
, but
$\mathcal {L} \models \Phi $
, but
![]() $\prod _C \mathcal {L} \not \models \Phi $
.
$\prod _C \mathcal {L} \not \models \Phi $
.
Corollary 4.9 may also be deduced from Lerman’s proof of Feferman, Scott, and Tennenbaum’s theorem that no cohesive power of the standard model of arithmetic is a model of Peano arithmetic (see [Reference Lerman16, Theorem 2.1]). Lerman uses Kleene’s T predicate to give a somewhat technical example of a
![]() $\Pi _3$
sentence that holds in the standard model of arithmetic but fails in every cohesive power. Our proof of Corollary 4.9 is more satisfying because it witnesses the optimality of Theorem 2.9 item (3) with a natural
$\Pi _3$
sentence that holds in the standard model of arithmetic but fails in every cohesive power. Our proof of Corollary 4.9 is more satisfying because it witnesses the optimality of Theorem 2.9 item (3) with a natural
![]() $\Pi _3$
sentence in the simple language of linear orders. In the next section, we enhance the construction of Theorem 4.8 to compute a copy
$\Pi _3$
sentence in the simple language of linear orders. In the next section, we enhance the construction of Theorem 4.8 to compute a copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
with
$\omega $
with
![]() $\prod _C \mathcal {L} \cong \omega + \eta $
under the additional assumption that the given cohesive set C is co-c.e.
$\prod _C \mathcal {L} \cong \omega + \eta $
under the additional assumption that the given cohesive set C is co-c.e.
Finally, we show that Theorem 2.7 concerning cohesive products is also tight by uniformly computing a sequence of finite linear orders
![]() $(\mathcal {L}_n : n \in \mathbb {N})$
such that for every cohesive set C, the cohesive product
$(\mathcal {L}_n : n \in \mathbb {N})$
such that for every cohesive set C, the cohesive product
![]() $\prod _C \mathcal {L}_n$
is a linear order with no maximum element. Thus the
$\prod _C \mathcal {L}_n$
is a linear order with no maximum element. Thus the
![]() $\Sigma _2$
sentence “there is a maximum element” is true in
$\Sigma _2$
sentence “there is a maximum element” is true in
![]() $\mathcal {L}_n$
for each n (because each
$\mathcal {L}_n$
for each n (because each
![]() $\mathcal {L}_n$
is finite), whereas the
$\mathcal {L}_n$
is finite), whereas the
![]() $\Pi _2$
sentence “there is no maximum element” is true in
$\Pi _2$
sentence “there is no maximum element” is true in
![]() $\prod _C \mathcal {L}_n$
for every cohesive set C. Although each linear order
$\prod _C \mathcal {L}_n$
for every cohesive set C. Although each linear order
![]() $\mathcal {L}_n$
has a maximum element, the sequence of maximum elements is not computable.
$\mathcal {L}_n$
has a maximum element, the sequence of maximum elements is not computable.
Proposition 4.10. There is a uniformly computable sequence of finite linear orders
![]() $(\mathcal {L}_n : n \in \mathbb {N})$
such that for every cohesive set C, the cohesive product
$(\mathcal {L}_n : n \in \mathbb {N})$
such that for every cohesive set C, the cohesive product
![]() $\prod _C \mathcal {L}_n$
is a linear order with no maximum element. Therefore Theorem 2.7 cannot be improved in general.
$\prod _C \mathcal {L}_n$
is a linear order with no maximum element. Therefore Theorem 2.7 cannot be improved in general.
Proof For each n, let
![]() $\mathcal {L}_n = (L_n, \prec )$
be the linear order with domain
$\mathcal {L}_n = (L_n, \prec )$
be the linear order with domain
that is ordered by the usual order by taking
![]() $\prec $
equal to
$\prec $
equal to
![]() $<$
on
$<$
on
![]() $L_n$
. To compute whether a given
$L_n$
. To compute whether a given
![]() $t> 0$
is in
$t> 0$
is in
![]() $L_n$
, first run
$L_n$
, first run
![]() $\varphi _e(n)$
for t steps for each
$\varphi _e(n)$
for t steps for each
![]() $e < n$
. Then for each such
$e < n$
. Then for each such
![]() $\varphi _e(n)$
that halts within t steps, find the s such that
$\varphi _e(n)$
that halts within t steps, find the s such that
![]() $\varphi _e(n)$
halts in exactly s steps, and compute the number
$\varphi _e(n)$
halts in exactly s steps, and compute the number
![]() $s + \varphi _e(n) + 1$
. If any of these numbers is t, then
$s + \varphi _e(n) + 1$
. If any of these numbers is t, then
![]() $t \in L_n$
. Otherwise
$t \in L_n$
. Otherwise
![]() $t \notin L_n$
. Notice that each
$t \notin L_n$
. Notice that each
![]() $e < n$
contributes at most one element t to
$e < n$
contributes at most one element t to
![]() $L_n$
, so
$L_n$
, so
![]() $\mathcal {L}_n$
has at most
$\mathcal {L}_n$
has at most
![]() $1 + n$
elements.
$1 + n$
elements.
Let C be cohesive, and consider an element
![]() $[\varphi _e]$
of
$[\varphi _e]$
of
![]() $\prod _C \mathcal {L}_n$
. We show that
$\prod _C \mathcal {L}_n$
. We show that
![]() $[\varphi _e]$
is not the
$[\varphi _e]$
is not the
![]() $\prec _{\prod _C \mathcal {L}_n}$
-greatest element of
$\prec _{\prod _C \mathcal {L}_n}$
-greatest element of
![]() $\prod _C \mathcal {L}_n$
and therefore that
$\prod _C \mathcal {L}_n$
and therefore that
![]() $\prod _C \mathcal {L}_n$
has no
$\prod _C \mathcal {L}_n$
has no
![]() $\prec _{\prod _C \mathcal {L}_n}$
-greatest element. If
$\prec _{\prod _C \mathcal {L}_n}$
-greatest element. If
![]() $n> e$
is a sufficiently large member of C, then
$n> e$
is a sufficiently large member of C, then
![]() $\varphi _e(n){\downarrow } \in L_n$
. This means that there is a least s such that
$\varphi _e(n){\downarrow } \in L_n$
. This means that there is a least s such that
![]() $\varphi _{e,s}(n){\downarrow }$
and therefore that there is a
$\varphi _{e,s}(n){\downarrow }$
and therefore that there is a
![]() $t \in L_n$
with
$t \in L_n$
with
![]() $\varphi _e(n) \prec t$
. Thus
$\varphi _e(n) \prec t$
. Thus
![]() $(\forall ^\infty n \in C)(\mathcal {L}_n \models \exists x\, (\varphi _e(n) \prec x))$
, so
$(\forall ^\infty n \in C)(\mathcal {L}_n \models \exists x\, (\varphi _e(n) \prec x))$
, so
![]() $\prod _C \mathcal {L}_n \models \exists x ([\varphi _e] \prec x)$
by Theorem 2.7 item (3). That is,
$\prod _C \mathcal {L}_n \models \exists x ([\varphi _e] \prec x)$
by Theorem 2.7 item (3). That is,
![]() $[\varphi _e]$
is not the
$[\varphi _e]$
is not the
![]() $\prec _{\prod _C \mathcal {L}_n}$
-greatest element of
$\prec _{\prod _C \mathcal {L}_n}$
-greatest element of
![]() $\prod _C \mathcal {L}_n$
.
$\prod _C \mathcal {L}_n$
.
5 A computable copy of
 $\omega $
with a cohesive power of order-type
$\omega $
with a cohesive power of order-type
 $\omega + \eta $
$\omega + \eta $
Given a co-c.e. cohesive set, we compute a copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
for which
$\omega $
for which
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \eta $
. In order to help shuffle various linear orders into cohesive powers in Section 6, we in fact compute a linear order
$\omega + \eta $
. In order to help shuffle various linear orders into cohesive powers in Section 6, we in fact compute a linear order
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
along with a coloring function
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
along with a coloring function
![]() $F \colon L \rightarrow \mathbb {N}$
that colors the elements of
$F \colon L \rightarrow \mathbb {N}$
that colors the elements of
![]() $\mathcal {L}$
with countably many colors so as to induce a coloring with a certain density property on
$\mathcal {L}$
with countably many colors so as to induce a coloring with a certain density property on
![]() $\prod _C \mathcal {L}$
.
$\prod _C \mathcal {L}$
.
Definition 5.1. A colored linear order is a structure
![]() $\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
, where
$\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
, where
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
is a linear order and F is (the graph of) a function
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
is a linear order and F is (the graph of) a function
![]() $F \colon L \rightarrow \mathbb {N}$
, thought of as a coloring of L. Here the language includes unary relation symbols for L and
$F \colon L \rightarrow \mathbb {N}$
, thought of as a coloring of L. Here the language includes unary relation symbols for L and
![]() $\mathbb {N}$
and a binary relation symbol for F in addition to the binary relation symbol
$\mathbb {N}$
and a binary relation symbol for F in addition to the binary relation symbol
![]() $\prec $
.
$\prec $
.
Let
![]() $\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
be a colored linear order, and let
$\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
be a colored linear order, and let
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
. We may think of
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
. We may think of
![]() $\mathcal {O}$
as the disjoint union
$\mathcal {O}$
as the disjoint union
![]() $\mathcal {L} \sqcup \mathbb {N}$
expanded to include F. Thus if
$\mathcal {L} \sqcup \mathbb {N}$
expanded to include F. Thus if
![]() $\mathcal {O}$
is a computable colored linear order and C is a cohesive set, then the cohesive power
$\mathcal {O}$
is a computable colored linear order and C is a cohesive set, then the cohesive power
![]() $\prod _C \mathcal {O}$
consists of a linear order
$\prod _C \mathcal {O}$
consists of a linear order
![]() $\prod _C \mathcal {L}$
, a set
$\prod _C \mathcal {L}$
, a set
![]() $\prod _C \mathbb {N}$
thought of as a collection of colors, and a (graph of a) function
$\prod _C \mathbb {N}$
thought of as a collection of colors, and a (graph of a) function
![]() $F^{\prod _C \mathcal {O}} \colon |\prod _C \mathcal {L}| \rightarrow |\prod _C \mathbb {N}|$
thought of as a coloring of
$F^{\prod _C \mathcal {O}} \colon |\prod _C \mathcal {L}| \rightarrow |\prod _C \mathbb {N}|$
thought of as a coloring of
![]() $\prod _C \mathcal {L}$
. This is by Proposition 2.14 and by Theorem 2.9 item (2), as F being the graph of a function from the substructure given by L into the substructure given by
$\prod _C \mathcal {L}$
. This is by Proposition 2.14 and by Theorem 2.9 item (2), as F being the graph of a function from the substructure given by L into the substructure given by
![]() $\mathbb {N}$
can be expressed by a
$\mathbb {N}$
can be expressed by a
![]() $\Pi _2$
sentence. In
$\Pi _2$
sentence. In
![]() $\prod _C \mathcal {O}$
, we denote elements of
$\prod _C \mathcal {O}$
, we denote elements of
![]() $\prod _C \mathcal {L}$
by
$\prod _C \mathcal {L}$
by
![]() $[\varphi ]$
and elements of
$[\varphi ]$
and elements of
![]() $\prod _C \mathbb {N}$
by
$\prod _C \mathbb {N}$
by
![]() . Call a color
. Call a color
![]() a solid color if
a solid color if
![]() $\delta $
is eventually constant on C (i.e., if
$\delta $
is eventually constant on C (i.e., if
![]() is in the range of the canonical embedding of
is in the range of the canonical embedding of
![]() $\mathbb {N}$
into
$\mathbb {N}$
into
![]() $\prod _C \mathbb {N}$
). Otherwise, call
$\prod _C \mathbb {N}$
). Otherwise, call
![]() a striped color. Finally, call a colored linear order
a striped color. Finally, call a colored linear order
![]() $\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
a colored copy of
$\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
a colored copy of
![]() $\omega $
if
$\omega $
if
![]() $\mathcal {L} \cong \omega $
.
$\mathcal {L} \cong \omega $
.
Definition 5.2. Let
![]() $\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
be a computable colored copy of
$\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
be a computable colored copy of
![]() $\omega $
, and let
$\omega $
, and let
![]() $\mathcal {L}$
denote
$\mathcal {L}$
denote
![]() $(L, \prec _{\mathcal {L}})$
. Let C be a cohesive set. Call the cohesive power
$(L, \prec _{\mathcal {L}})$
. Let C be a cohesive set. Call the cohesive power
![]() $\prod _C \mathcal {O}$
colorful if the following items hold.
$\prod _C \mathcal {O}$
colorful if the following items hold.
-
• For every pair of non-standard elements
 $[\varphi ], [\psi ] \in |\prod _C \mathcal {L}|$
with
$[\varphi ], [\psi ] \in |\prod _C \mathcal {L}|$
with
 $[\psi ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
and every solid color
$[\psi ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
and every solid color
 , there is a
, there is a
 $[\theta ] \in |\prod _C \mathcal {L}|$
with
$[\theta ] \in |\prod _C \mathcal {L}|$
with
 $[\psi ] \prec _{\prod _C \mathcal {L}} [\theta ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
and
$[\psi ] \prec _{\prod _C \mathcal {L}} [\theta ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
and
 .
. -
• For every pair of non-standard elements
 $[\varphi ], [\psi ] \in |\prod _C \mathcal {L}|$
with
$[\varphi ], [\psi ] \in |\prod _C \mathcal {L}|$
with
 $[\psi ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
, there is a
$[\psi ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
, there is a
 $[\theta ] \in |\prod _C \mathcal {L}|$
with
$[\theta ] \in |\prod _C \mathcal {L}|$
with
 $[\psi ] \prec _{\prod _C \mathcal {L}} [\theta ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
where
$[\psi ] \prec _{\prod _C \mathcal {L}} [\theta ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
where
 $F^{\prod _C \mathcal {O}}([\theta ])$
is a striped color.
$F^{\prod _C \mathcal {O}}([\theta ])$
is a striped color.
Thus if
![]() $\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
is a computable colored copy of
$\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
is a computable colored copy of
![]() $\omega $
and C is cohesive, then
$\omega $
and C is cohesive, then
![]() $\prod _C \mathcal {O}$
being colorful means that the solid colors occur densely in the non-standard part of
$\prod _C \mathcal {O}$
being colorful means that the solid colors occur densely in the non-standard part of
![]() $\prod _C \mathcal {L}$
and also that between any two elements of the non-standard part of
$\prod _C \mathcal {L}$
and also that between any two elements of the non-standard part of
![]() $\prod _C \mathcal {L}$
there is an element with a striped color. Notice that we do not require any individual striped color to occur densely in the non-standard part of
$\prod _C \mathcal {L}$
there is an element with a striped color. Notice that we do not require any individual striped color to occur densely in the non-standard part of
![]() $\prod _C \mathcal {L}$
. If C is a co-c.e. cohesive set, then the first bullet of Definition 5.2 implies the second. This can be seen by a saturation argument, if one generalizes Lemma 2.17 to allow types over
$\prod _C \mathcal {L}$
. If C is a co-c.e. cohesive set, then the first bullet of Definition 5.2 implies the second. This can be seen by a saturation argument, if one generalizes Lemma 2.17 to allow types over
![]() $\prod _C \mathcal {O}$
with an infinite sequence of parameters
$\prod _C \mathcal {O}$
with an infinite sequence of parameters
![]() $([\theta _i] : i \in \mathbb {N})$
represented by a uniformly partial computable sequence
$([\theta _i] : i \in \mathbb {N})$
represented by a uniformly partial computable sequence
![]() $(\theta _i : i \in \mathbb {N})$
. Here the relevant parameters would be the non-standard elements
$(\theta _i : i \in \mathbb {N})$
. Here the relevant parameters would be the non-standard elements
![]() $[\varphi ]$
and
$[\varphi ]$
and
![]() $[\psi ]$
and the sequence of solid colors. The type would then describe an element between
$[\psi ]$
and the sequence of solid colors. The type would then describe an element between
![]() $[\varphi ]$
and
$[\varphi ]$
and
![]() $[\psi ]$
whose color is not among the solid colors.
$[\psi ]$
whose color is not among the solid colors.
In Section 6, we show that replacing each point of
![]() $\mathcal {L}$
by some finite linear order depending on its color has the effect of shuffling these finite orders into the non-standard part of
$\mathcal {L}$
by some finite linear order depending on its color has the effect of shuffling these finite orders into the non-standard part of
![]() $\prod _C \mathcal {L}$
.
$\prod _C \mathcal {L}$
.
Theorem 5.3. Let C be a co-c.e. cohesive set. Then there is a computable colored copy
![]() $\mathcal {O}$
of
$\mathcal {O}$
of
![]() $\omega $
such that
$\omega $
such that
![]() $\prod _C \mathcal {O}$
is colorful.
$\prod _C \mathcal {O}$
is colorful.
Proof We construct a computable copy
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
of
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
of
![]() $\omega $
with
$\omega $
with
![]() $L = \mathbb {N}$
and a function
$L = \mathbb {N}$
and a function
![]() $F \colon L \rightarrow \mathbb {N}$
so that
$F \colon L \rightarrow \mathbb {N}$
so that
![]() $\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
is a computable colored copy of
$\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
is a computable colored copy of
![]() $\omega $
for which
$\omega $
for which
![]() $\prod _C \mathcal {O}$
is colorful. We are working with a co-c.e. cohesive set, so recall that in this situation every element
$\prod _C \mathcal {O}$
is colorful. We are working with a co-c.e. cohesive set, so recall that in this situation every element
![]() $[\varphi ]$
of
$[\varphi ]$
of
![]() $\prod _C \mathcal {L}$
has a total computable representative by the discussion following Definition 2.2. Recall also that an element
$\prod _C \mathcal {L}$
has a total computable representative by the discussion following Definition 2.2. Recall also that an element
![]() $[\varphi ]$
of
$[\varphi ]$
of
![]() $\prod _C \mathcal {L}$
is non-standard if and only if
$\prod _C \mathcal {L}$
is non-standard if and only if
![]() $\lim _{n \in C}\varphi (n) = \infty $
by Lemma 4.2.
$\lim _{n \in C}\varphi (n) = \infty $
by Lemma 4.2.
The goal of the construction is to arrange, for every pair of total computable functions
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
with
$\psi $
with
![]() $\lim _{n \in C}\varphi (n) = \lim _{n \in C}\psi (n) = \infty $
, that
$\lim _{n \in C}\varphi (n) = \lim _{n \in C}\psi (n) = \infty $
, that
 $$ \begin{align} (\forall^\infty n \in C)\Bigl( &\psi(n){\downarrow} \prec_{\mathcal{L}} \varphi(n){\downarrow}\\&\Rightarrow\; \bigl( \forall d \leq \max\nolimits_<\{\varphi(n), \psi(n)\} \bigr) \bigl( \exists k \bigr) \bigl[(\psi(n) \prec_{\mathcal{L}} k \prec_{\mathcal{L}} \varphi(n)) \,\wedge\, (F(k) = d) \bigr]\Bigr).\nonumber \end{align} $$
$$ \begin{align} (\forall^\infty n \in C)\Bigl( &\psi(n){\downarrow} \prec_{\mathcal{L}} \varphi(n){\downarrow}\\&\Rightarrow\; \bigl( \forall d \leq \max\nolimits_<\{\varphi(n), \psi(n)\} \bigr) \bigl( \exists k \bigr) \bigl[(\psi(n) \prec_{\mathcal{L}} k \prec_{\mathcal{L}} \varphi(n)) \,\wedge\, (F(k) = d) \bigr]\Bigr).\nonumber \end{align} $$
Suppose we achieve (*) for
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
, where
$\psi $
, where
![]() $\lim _{n \in C}\varphi (n) = \lim _{n \in C}\psi (n) = \infty $
and
$\lim _{n \in C}\varphi (n) = \lim _{n \in C}\psi (n) = \infty $
and
![]() $(\forall ^\infty n \in C)(\psi (n){\downarrow } \prec _{\mathcal {L}} \varphi (n){\downarrow })$
. Fix any color d, and let
$(\forall ^\infty n \in C)(\psi (n){\downarrow } \prec _{\mathcal {L}} \varphi (n){\downarrow })$
. Fix any color d, and let
![]() $\delta $
be the constant function with value d. Partially compute a function
$\delta $
be the constant function with value d. Partially compute a function
![]() $\theta (n)$
by searching for a k with
$\theta (n)$
by searching for a k with
![]() $\psi (n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi (n)$
and
$\psi (n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi (n)$
and
![]() $F(k) = d$
. If there is such a k, let
$F(k) = d$
. If there is such a k, let
![]() $\theta (n)$
be the first such k. Property (*) and the assumption
$\theta (n)$
be the first such k. Property (*) and the assumption
![]() $\lim _{n \in C}\varphi (n) = \lim _{n \in C}\psi (n) = \infty $
ensure that there is such a k for almost every
$\lim _{n \in C}\varphi (n) = \lim _{n \in C}\psi (n) = \infty $
ensure that there is such a k for almost every
![]() $n \in C$
. Therefore
$n \in C$
. Therefore
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
,
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
,
![]() $[\psi ] \prec _{\prod _C \mathcal {L}} [\theta ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
, and
$[\psi ] \prec _{\prod _C \mathcal {L}} [\theta ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
, and
![]() . Likewise, we could instead define
. Likewise, we could instead define
![]() $\theta (n)$
to search for a k with
$\theta (n)$
to search for a k with
![]() $\psi (n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi (n)$
and
$\psi (n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi (n)$
and
![]() $F(k) = \varphi (n)$
and let
$F(k) = \varphi (n)$
and let
![]() $\theta (n)$
be the first (if any) such k found. In this case we would have
$\theta (n)$
be the first (if any) such k found. In this case we would have
![]() $[\psi ] \prec _{\prod _C \mathcal {L}} [\theta ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
and
$[\psi ] \prec _{\prod _C \mathcal {L}} [\theta ] \prec _{\prod _C \mathcal {L}} [\varphi ]$
and
![]() , which is a striped color because
, which is a striped color because
![]() $\lim _{n \in C}\varphi (n) = \infty $
. Notice that
$\lim _{n \in C}\varphi (n) = \infty $
. Notice that
![]() $\varphi $
represents both an element
$\varphi $
represents both an element
![]() $[\varphi ]$
of the linear order
$[\varphi ]$
of the linear order
![]() $\prod _C \mathcal {L}$
and a color
$\prod _C \mathcal {L}$
and a color
![]() from
from
![]() $\prod _C \mathbb {N}$
. As a color,
$\prod _C \mathbb {N}$
. As a color,
![]() because
because
![]() $(\forall ^\infty n \in C)(F(\theta (n)) = \varphi (n))$
. Thus between
$(\forall ^\infty n \in C)(F(\theta (n)) = \varphi (n))$
. Thus between
![]() $[\psi ]$
and
$[\psi ]$
and
![]() $[\varphi ]$
there are elements of
$[\varphi ]$
there are elements of
![]() $\prod _C \mathcal {L}$
of every solid color and also at least one element of a striped color. Therefore achieving (*) suffices to prove the theorem, provided we also arrange
$\prod _C \mathcal {L}$
of every solid color and also at least one element of a striped color. Therefore achieving (*) suffices to prove the theorem, provided we also arrange
![]() $\mathcal {L} \cong \omega $
.
$\mathcal {L} \cong \omega $
.
Let W denote the c.e. set
![]() $\overline {C}$
, and let
$\overline {C}$
, and let
![]() $(W_s)_{s \in \mathbb {N}}$
be a computable
$(W_s)_{s \in \mathbb {N}}$
be a computable
![]() $\subseteq $
-increasing enumeration of W. Let
$\subseteq $
-increasing enumeration of W. Let
![]() $(A^{i,0}, A^{i,1})_{i \in \mathbb {N}}$
be a uniformly computable sequence of pairs of sets such that:
$(A^{i,0}, A^{i,1})_{i \in \mathbb {N}}$
be a uniformly computable sequence of pairs of sets such that:
-
• for each i,
 $A^{i,0}$
and
$A^{i,0}$
and
 $A^{i,1}$
partition
$A^{i,1}$
partition
 $\mathbb {N}$
into two pieces (i.e.,
$\mathbb {N}$
into two pieces (i.e.,
 $A^{i,1} = \overline {A^{i,0}}$
) and
$A^{i,1} = \overline {A^{i,0}}$
) and -
•
 $(\forall n)(\forall \sigma \in \{0,1\}^n)\bigl (\bigcap _{i < n} A^{i, \sigma (i)}\text { is infinite}\bigr )$
.
$(\forall n)(\forall \sigma \in \{0,1\}^n)\bigl (\bigcap _{i < n} A^{i, \sigma (i)}\text { is infinite}\bigr )$
.
This can be accomplished by partitioning
![]() $\mathbb {N}$
into successive pieces of size
$\mathbb {N}$
into successive pieces of size
![]() $2^i$
, letting
$2^i$
, letting
![]() $A^{i,0}$
consist of every other piece, and letting
$A^{i,0}$
consist of every other piece, and letting
![]() $A^{i,1} = \overline {A^{i,0}}$
.
$A^{i,1} = \overline {A^{i,0}}$
.
In this proof, denote the projection functions associated with the pairing function
![]() $\langle \cdot , \cdot \rangle $
by
$\langle \cdot , \cdot \rangle $
by
![]() $\ell $
and r, for left and right, instead of by
$\ell $
and r, for left and right, instead of by
![]() $\pi _0$
and
$\pi _0$
and
![]() $\pi _1$
. So
$\pi _1$
. So
![]() $\ell (\langle x, y \rangle ) = x$
and
$\ell (\langle x, y \rangle ) = x$
and
![]() $r(\langle x, y \rangle ) = y$
.
$r(\langle x, y \rangle ) = y$
.
The tension in the construction is between achieving (*) and ensuring that for every z, there are only finitely many x with
![]() $x \prec _{\mathcal {L}} z$
. Think of a
$x \prec _{\mathcal {L}} z$
. Think of a
![]() $p \in \mathbb {N}$
as coding a pair
$p \in \mathbb {N}$
as coding a pair
![]() $(\varphi _{\ell (p)}, \varphi _{r(p)})$
of partial computable functions for which we would like to achieve (*), with
$(\varphi _{\ell (p)}, \varphi _{r(p)})$
of partial computable functions for which we would like to achieve (*), with
![]() $\varphi _{\ell (p)}$
playing the role of
$\varphi _{\ell (p)}$
playing the role of
![]() $\psi $
and
$\psi $
and
![]() $\varphi _{r(p)}$
playing the role of
$\varphi _{r(p)}$
playing the role of
![]() $\varphi $
. We assign the partition
$\varphi $
. We assign the partition
![]() $(A^{2p,0}, A^{2p,1})$
to
$(A^{2p,0}, A^{2p,1})$
to
![]() $\varphi _{\ell (p)}$
and the partition
$\varphi _{\ell (p)}$
and the partition
![]() $(A^{2p+1,0}, A^{2p+1,1})$
to
$(A^{2p+1,0}, A^{2p+1,1})$
to
![]() $\varphi _{r(p)}$
. The sets
$\varphi _{r(p)}$
. The sets
![]() $\{n : \varphi _{\ell (p)}(n) \in A^{2p,0}\}$
and
$\{n : \varphi _{\ell (p)}(n) \in A^{2p,0}\}$
and
![]() $\{n : \varphi _{\ell (p)}(n) \in A^{2p,1}\}$
are both c.e., so if
$\{n : \varphi _{\ell (p)}(n) \in A^{2p,1}\}$
are both c.e., so if
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi _{\ell (p)})$
, then either
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi _{\ell (p)})$
, then either
![]() $(\forall ^\infty n \in C)(\varphi _{\ell (p)}(n) \in A^{2p,0})$
or
$(\forall ^\infty n \in C)(\varphi _{\ell (p)}(n) \in A^{2p,0})$
or
![]() $(\forall ^\infty n \in C)(\varphi _{\ell (p)}(n) \in A^{2p,1})$
; and similarly for
$(\forall ^\infty n \in C)(\varphi _{\ell (p)}(n) \in A^{2p,1})$
; and similarly for
![]() $\varphi _{r(p)}$
and
$\varphi _{r(p)}$
and
![]() $(A^{2p+1,0}, A^{2p+1,1})$
. As the construction proceeds, we consider each p paired with larger and larger guesses N of a threshold by which the cohesive behavior of
$(A^{2p+1,0}, A^{2p+1,1})$
. As the construction proceeds, we consider each p paired with larger and larger guesses N of a threshold by which the cohesive behavior of
![]() $\varphi _{\ell (p)}$
and
$\varphi _{\ell (p)}$
and
![]() $\varphi _{r(p)}$
begins with respect to the partitions
$\varphi _{r(p)}$
begins with respect to the partitions
![]() $(A^{2p,0}, A^{2p,1})$
and
$(A^{2p,0}, A^{2p,1})$
and
![]() $(A^{2p+1,0}, A^{2p+1,1})$
. The pair
$(A^{2p+1,0}, A^{2p+1,1})$
. The pair
![]() $\langle p, N \rangle $
means we guess that there is an
$\langle p, N \rangle $
means we guess that there is an
![]() $(a,b) \in \{0,1\} \times \{0,1\}$
such that
$(a,b) \in \{0,1\} \times \{0,1\}$
such that
![]() $\varphi _{\ell (p)}(n) \in A^{2p,a}$
and
$\varphi _{\ell (p)}(n) \in A^{2p,a}$
and
![]() $\varphi _{r(p)}(n) \in A^{2p+1,b}$
whenever
$\varphi _{r(p)}(n) \in A^{2p+1,b}$
whenever
![]() $n \geq N$
and
$n \geq N$
and
![]() $n \in C$
. For each fixed p, the pairs
$n \in C$
. For each fixed p, the pairs
![]() $\langle p, 0 \rangle , \langle p, 1 \rangle , \langle p, 2 \rangle , \dots $
all try to achieve (*) for
$\langle p, 0 \rangle , \langle p, 1 \rangle , \langle p, 2 \rangle , \dots $
all try to achieve (*) for
![]() $\varphi _{\ell (p)}$
and
$\varphi _{\ell (p)}$
and
![]() $\varphi _{r(p)}$
. If N is too small, then pair
$\varphi _{r(p)}$
. If N is too small, then pair
![]() $\langle p , N \rangle $
eventually stops acting. If N is big enough, then pair
$\langle p , N \rangle $
eventually stops acting. If N is big enough, then pair
![]() $\langle p, N \rangle $
eventually settles on the correct sides
$\langle p, N \rangle $
eventually settles on the correct sides
![]() $(a, b)$
of the partitions
$(a, b)$
of the partitions
![]() $(A^{2p,0}, A^{2p,1})$
and
$(A^{2p,0}, A^{2p,1})$
and
![]() $(A^{2p+1,0}, A^{2p+1,1})$
.
$(A^{2p+1,0}, A^{2p+1,1})$
.
To help satisfy (*), eventually pair
![]() $\langle p, N \rangle $
will want to add an element
$\langle p, N \rangle $
will want to add an element
![]() $k_0$
between some
$k_0$
between some
![]() $\varphi _{\ell (p)}(n)$
and
$\varphi _{\ell (p)}(n)$
and
![]() $\varphi _{r(p)}(n)$
for an n that looks like it may be in C. However, later some pair
$\varphi _{r(p)}(n)$
for an n that looks like it may be in C. However, later some pair
![]() $\langle q, M \rangle $
(possibly even with
$\langle q, M \rangle $
(possibly even with
![]() $q = p$
) may want to add an element
$q = p$
) may want to add an element
![]() $k_1$
between some
$k_1$
between some
![]() $\varphi _{\ell (q)}(m)$
and
$\varphi _{\ell (q)}(m)$
and
![]() $\varphi _{r(q)}(m)$
for an m that looks like it may be in C, and it may also so happen that
$\varphi _{r(q)}(m)$
for an m that looks like it may be in C, and it may also so happen that
![]() $\varphi _{r(q)}(m) = k_0$
. In this case,
$\varphi _{r(q)}(m) = k_0$
. In this case,
![]() $\langle q, M \rangle $
would add
$\langle q, M \rangle $
would add
![]() $k_1 \prec _{\mathcal {L}} k_0$
. If this behavior were to continue, then it would lead to a descending sequence
$k_1 \prec _{\mathcal {L}} k_0$
. If this behavior were to continue, then it would lead to a descending sequence
![]() $k_0 \succ _{\mathcal {L}} k_1 \succ _{\mathcal {L}} k_2 \succ _{\mathcal {L}} \cdots $
, which means that
$k_0 \succ _{\mathcal {L}} k_1 \succ _{\mathcal {L}} k_2 \succ _{\mathcal {L}} \cdots $
, which means that
![]() $\mathcal {L}$
would not have order-type
$\mathcal {L}$
would not have order-type
![]() $\omega $
. To avoid these descending sequences, pair
$\omega $
. To avoid these descending sequences, pair
![]() $\langle p, N \rangle $
tries to choose the k that it adds to avoid the images
$\langle p, N \rangle $
tries to choose the k that it adds to avoid the images
![]() $\varphi _{\ell (q)}(C)$
and
$\varphi _{\ell (q)}(C)$
and
![]() $\varphi _{r(q)}(C)$
for all q corresponding to higher-or-equal priority pairs
$\varphi _{r(q)}(C)$
for all q corresponding to higher-or-equal priority pairs
![]() $\langle q, M \rangle \leq \langle p, N \rangle $
. To do this, first, for each such q, pair
$\langle q, M \rangle \leq \langle p, N \rangle $
. To do this, first, for each such q, pair
![]() $\langle p, N \rangle $
looks up the most recent guess
$\langle p, N \rangle $
looks up the most recent guess
![]() $(a_q, b_q)$
of sides such that
$(a_q, b_q)$
of sides such that
![]() $\varphi _{\ell (q)}(C) \subseteq ^* A^{2q, a_q}$
and
$\varphi _{\ell (q)}(C) \subseteq ^* A^{2q, a_q}$
and
![]() $\varphi _{r(q)}(C) \subseteq ^* A^{2q+1, b_q}$
made by any of the
$\varphi _{r(q)}(C) \subseteq ^* A^{2q+1, b_q}$
made by any of the
![]() $\langle q, M \rangle \leq \langle p, N \rangle $
for this q. Then pair
$\langle q, M \rangle \leq \langle p, N \rangle $
for this q. Then pair
![]() $\langle p, N \rangle $
chooses
$\langle p, N \rangle $
chooses
from the opposite sides of all these partitions in an attempt to avoid
![]() $\varphi _{\ell (q)}(C)$
and
$\varphi _{\ell (q)}(C)$
and
![]() $\varphi _{r(q)}(C)$
for every
$\varphi _{r(q)}(C)$
for every
![]() $\langle q, M \rangle \leq \langle p, N \rangle $
. The staggering of the partitions ensures that there are infinitely many such k to choose among.
$\langle q, M \rangle \leq \langle p, N \rangle $
. The staggering of the partitions ensures that there are infinitely many such k to choose among.
We now give the construction. Define
![]() $\prec _{\mathcal {L}}$
and F in stages. By the end of stage s,
$\prec _{\mathcal {L}}$
and F in stages. By the end of stage s,
![]() $\prec _{\mathcal {L}}$
will have been defined on
$\prec _{\mathcal {L}}$
will have been defined on
![]() $X_s \times X_s$
, and F will have been defined on
$X_s \times X_s$
, and F will have been defined on
![]() $X_s$
for some finite
$X_s$
for some finite
![]() $X_s \supseteq \{0, 1, \dots , s\}$
.
$X_s \supseteq \{0, 1, \dots , s\}$
.
At stage
![]() $0$
, set
$0$
, set
![]() $X_0 = \{0\}$
with
$X_0 = \{0\}$
with
![]() $0 \nprec _{\mathcal {L}} 0$
and
$0 \nprec _{\mathcal {L}} 0$
and
![]() $F(0) = 0$
. At stage
$F(0) = 0$
. At stage
![]() $s> 0$
, initially set
$s> 0$
, initially set
![]() $X_s = X_{s-1}$
. If
$X_s = X_{s-1}$
. If
![]() $s \notin X_s$
, then add s to
$s \notin X_s$
, then add s to
![]() $X_s$
, define it to be the
$X_s$
, define it to be the
![]() $\prec _{\mathcal {L}}$
-maximum element of
$\prec _{\mathcal {L}}$
-maximum element of
![]() $X_s$
, and define
$X_s$
, and define
![]() $F(s) = 0$
. Then proceed as follows.
$F(s) = 0$
. Then proceed as follows.
Consider each pair
![]() $\langle p, N \rangle < s$
in order. Think of
$\langle p, N \rangle < s$
in order. Think of
![]() $\langle p, N \rangle $
as coding a pair
$\langle p, N \rangle $
as coding a pair
![]() $(\varphi _{\ell (p)}, \varphi _{r(p)})$
of partial computable functions and a guess N of a threshold by which the cohesive behavior of
$(\varphi _{\ell (p)}, \varphi _{r(p)})$
of partial computable functions and a guess N of a threshold by which the cohesive behavior of
![]() $\varphi _{\ell (p)}$
and
$\varphi _{\ell (p)}$
and
![]() $\varphi _{r(p)}$
begins with respect to the partitions
$\varphi _{r(p)}$
begins with respect to the partitions
![]() $(A^{2p,0}, A^{2p,1})$
and
$(A^{2p,0}, A^{2p,1})$
and
![]() $(A^{2p+1,0}, A^{2p+1,1})$
as described above. The pair
$(A^{2p+1,0}, A^{2p+1,1})$
as described above. The pair
![]() $\langle p, N \rangle $
demands action if there is an
$\langle p, N \rangle $
demands action if there is an
![]() $(a, b, n) \in \{0,1\} \times \{0,1\} \times \{N, N+1, \dots , s\}$
meeting the following conditions:
$(a, b, n) \in \{0,1\} \times \{0,1\} \times \{N, N+1, \dots , s\}$
meeting the following conditions:
-
(1) For all
 $m \leq n$
,
$m \leq n$
,
 $\varphi _{\ell (p),s}(m){\downarrow }$
and
$\varphi _{\ell (p),s}(m){\downarrow }$
and
 $\varphi _{r(p),s}(m){\downarrow }$
.
$\varphi _{r(p),s}(m){\downarrow }$
. -
(2) Both
 $\varphi _{\ell (p)}(n) \in A^{2p, a}$
and
$\varphi _{\ell (p)}(n) \in A^{2p, a}$
and
 $\varphi _{r(p)}(n) \in A^{2p+1, b}$
.
$\varphi _{r(p)}(n) \in A^{2p+1, b}$
. -
(3) For all m with
 $N \leq m \leq n$
:
$N \leq m \leq n$
:-
•
 $\varphi _{\ell (p)}(m) \in A^{2p, 1-a} \;\Rightarrow \; m \in W_s$
, and
$\varphi _{\ell (p)}(m) \in A^{2p, 1-a} \;\Rightarrow \; m \in W_s$
, and -
•
 $\varphi _{r(p)}(m) \in A^{2p+1, 1-b} \;\Rightarrow \; m \in W_s$
.
$\varphi _{r(p)}(m) \in A^{2p+1, 1-b} \;\Rightarrow \; m \in W_s$
.
-
-
(4) We have that
 $\varphi _{\ell (p)}(n), \varphi _{r(p)}(n) \in X_s$
and
$\varphi _{\ell (p)}(n), \varphi _{r(p)}(n) \in X_s$
and
 $\varphi _{\ell (p)}(n) \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
, but currently there is a
$\varphi _{\ell (p)}(n) \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
, but currently there is a
 $d \leq \max _<\{\varphi _{\ell (p)}(n), \varphi _{r(p)}(n)\}$
for which there is no
$d \leq \max _<\{\varphi _{\ell (p)}(n), \varphi _{r(p)}(n)\}$
for which there is no
 $k \in X_s$
with
$k \in X_s$
with
 $\varphi _{\ell (p)}(n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
and
$\varphi _{\ell (p)}(n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
and
 $F(k) = d$
.
$F(k) = d$
. -
(5) The element
 $\varphi _{\ell (p)}(n)$
is not
$\varphi _{\ell (p)}(n)$
is not
 $\preceq _{\mathcal {L}}$
-below any of
$\preceq _{\mathcal {L}}$
-below any of
 $0, 1, \dots , \langle p, N \rangle $
.
$0, 1, \dots , \langle p, N \rangle $
.
If
![]() $\langle p, N \rangle $
demands action, let
$\langle p, N \rangle $
demands action, let
![]() $(a_p, b_p, n) \in \{0,1\} \times \{0,1\} \times \{N, N+1, \dots , s\}$
be the lexicographically least witness to this, call
$(a_p, b_p, n) \in \{0,1\} \times \{0,1\} \times \{N, N+1, \dots , s\}$
be the lexicographically least witness to this, call
![]() $(a_p, b_p, n)$
the action witness for
$(a_p, b_p, n)$
the action witness for
![]() $\langle p, N \rangle $
, call the first two coordinates
$\langle p, N \rangle $
, call the first two coordinates
![]() $(a_p, b_p)$
of the action witness the action sides for
$(a_p, b_p)$
of the action witness the action sides for
![]() $\langle p, N \rangle $
, and call the last coordinate n of the action witness the action input for
$\langle p, N \rangle $
, and call the last coordinate n of the action witness the action input for
![]() $\langle p, N \rangle $
.
$\langle p, N \rangle $
.
Let r be the
![]() $<$
-greatest number for which there is an M with
$<$
-greatest number for which there is an M with
![]() $\langle r, M \rangle \leq \langle p, N \rangle $
. For each
$\langle r, M \rangle \leq \langle p, N \rangle $
. For each
![]() $q \leq r$
, let
$q \leq r$
, let
![]() $(a_q, b_q)$
be the most recently used action sides by any pair of the form
$(a_q, b_q)$
be the most recently used action sides by any pair of the form
![]() $\langle q, M \rangle $
with
$\langle q, M \rangle $
with
![]() $\langle q, M \rangle \leq \langle p, N \rangle $
. If no
$\langle q, M \rangle \leq \langle p, N \rangle $
. If no
![]() $\langle q, M \rangle \leq \langle p, N \rangle $
has yet demanded action, then let
$\langle q, M \rangle \leq \langle p, N \rangle $
has yet demanded action, then let
![]() $(a_q, b_q) = (0, 0)$
. Let
$(a_q, b_q) = (0, 0)$
. Let
![]() $c = \max _<\{\varphi _{\ell (p)}(n), \varphi _{r(p)}(n)\}$
, and let
$c = \max _<\{\varphi _{\ell (p)}(n), \varphi _{r(p)}(n)\}$
, and let
![]() $k_0 < k_1 < \cdots < k_c$
be the
$k_0 < k_1 < \cdots < k_c$
be the
![]() $c+1$
least members of
$c+1$
least members of
 $$ \begin{align} \bigcap_{q \leq r}\left(A^{2q, 1-a_q} \cap A^{2q+1, 1-b_q}\right) \setminus X_s, \end{align} $$
$$ \begin{align} \bigcap_{q \leq r}\left(A^{2q, 1-a_q} \cap A^{2q+1, 1-b_q}\right) \setminus X_s, \end{align} $$
which exist because the intersection is infinite and
![]() $X_s$
is finite. Add
$X_s$
is finite. Add
![]() $k_0, \dots , k_c$
to
$k_0, \dots , k_c$
to
![]() $X_s$
. Let
$X_s$
. Let
![]() $x \in X_s$
be the current
$x \in X_s$
be the current
![]() $\prec _{\mathcal {L}}$
-greatest element of the interval
$\prec _{\mathcal {L}}$
-greatest element of the interval
![]() $(\varphi _{\ell (p)}(n), \varphi _{r(p)}(n))_{\mathcal {L}}$
(or
$(\varphi _{\ell (p)}(n), \varphi _{r(p)}(n))_{\mathcal {L}}$
(or
![]() $x = \varphi _{\ell (p)}(n)$
if the interval is empty), and set
$x = \varphi _{\ell (p)}(n)$
if the interval is empty), and set
Also set
![]() $F(k_i) = i$
for each
$F(k_i) = i$
for each
![]() $i \leq c$
, and say that
$i \leq c$
, and say that
![]() $\langle p, N \rangle $
has acted and added k’s. This completes the construction.
$\langle p, N \rangle $
has acted and added k’s. This completes the construction.
The constructed
![]() $\mathcal {L}$
is a computable linear order. We show that
$\mathcal {L}$
is a computable linear order. We show that
![]() $\mathcal {L} \cong \omega $
by showing that for each z, there are only finitely many elements
$\mathcal {L} \cong \omega $
by showing that for each z, there are only finitely many elements
![]() $\prec _{\mathcal {L}}$
-below z. So fix z. Note that z appears in
$\prec _{\mathcal {L}}$
-below z. So fix z. Note that z appears in
![]() $X_s$
at stage
$X_s$
at stage
![]() $s = z$
at the latest, so we consider the development of the construction at stages
$s = z$
at the latest, so we consider the development of the construction at stages
![]() $s> z$
.
$s> z$
.
Consider the actions of a pair
![]() $\langle p, N \rangle $
. If
$\langle p, N \rangle $
. If
![]() $\langle p, N \rangle \geq z$
and
$\langle p, N \rangle \geq z$
and
![]() $\langle p, N \rangle $
acts at stage
$\langle p, N \rangle $
acts at stage
![]() $s> z$
with action input n, then, by condition (5), it must be that
$s> z$
with action input n, then, by condition (5), it must be that
![]() $z \prec _{\mathcal {L}} \varphi _{\ell (p)}(n) \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
. In this case, the action adds elements to
$z \prec _{\mathcal {L}} \varphi _{\ell (p)}(n) \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
. In this case, the action adds elements to
![]() $X_s$
and places them
$X_s$
and places them
![]() $\prec _{\mathcal {L}}$
-between
$\prec _{\mathcal {L}}$
-between
![]() $\varphi _{\ell (p)}(n)$
and
$\varphi _{\ell (p)}(n)$
and
![]() $\varphi _{r(p)}(n)$
and hence places them
$\varphi _{r(p)}(n)$
and hence places them
![]() $\prec _{\mathcal {L}}$
-above z. Therefore, only the actions of
$\prec _{\mathcal {L}}$
-above z. Therefore, only the actions of
![]() $\langle p, N \rangle $
with
$\langle p, N \rangle $
with
![]() $\langle p, N \rangle < z$
can add elements
$\langle p, N \rangle < z$
can add elements
![]() $\prec _{\mathcal {L}}$
-below z at stages
$\prec _{\mathcal {L}}$
-below z at stages
![]() $s> z$
.
$s> z$
.
We show that each
![]() $\langle p, N \rangle < z$
only ever acts to add finitely many elements
$\langle p, N \rangle < z$
only ever acts to add finitely many elements
![]() $k \prec _{\mathcal {L}} z$
. It follows that there are only finitely many elements
$k \prec _{\mathcal {L}} z$
. It follows that there are only finitely many elements
![]() $\prec _{\mathcal {L}}$
-below z because the
$\prec _{\mathcal {L}}$
-below z because the
![]() $\langle p, N \rangle \geq z$
add no elements
$\langle p, N \rangle \geq z$
add no elements
![]() $\prec _{\mathcal {L}}$
-below z after stage z, and each
$\prec _{\mathcal {L}}$
-below z after stage z, and each
![]() $\langle p, N \rangle < z$
adds only finitely many elements
$\langle p, N \rangle < z$
adds only finitely many elements
![]() $\prec _{\mathcal {L}}$
-below z. So let
$\prec _{\mathcal {L}}$
-below z. So let
![]() $\langle p, N \rangle < z$
, and assume inductively that there is a stage
$\langle p, N \rangle < z$
, and assume inductively that there is a stage
![]() $s_0> z$
such that no pair
$s_0> z$
such that no pair
![]() $\langle q, M \rangle < \langle p, N \rangle $
acts to add elements
$\langle q, M \rangle < \langle p, N \rangle $
acts to add elements
![]() $k \prec _{\mathcal {L}} z$
after stage
$k \prec _{\mathcal {L}} z$
after stage
![]() $s_0$
.
$s_0$
.
Notice that a given n can be the action input for
![]() $\langle p, N \rangle $
at most once. If
$\langle p, N \rangle $
at most once. If
![]() $\langle p, N \rangle $
demands action with action input n at stage s, it adds elements of every color
$\langle p, N \rangle $
demands action with action input n at stage s, it adds elements of every color
![]() $\leq \max _<\{\varphi _{\ell (p)}(n), \varphi _{r(p)}(n)\}$
to
$\leq \max _<\{\varphi _{\ell (p)}(n), \varphi _{r(p)}(n)\}$
to
![]() $X_s$
and places them
$X_s$
and places them
![]() $\prec _{\mathcal {L}}$
-between
$\prec _{\mathcal {L}}$
-between
![]() $\varphi _{\ell (p)}(n)$
and
$\varphi _{\ell (p)}(n)$
and
![]() $\varphi _{r(p)}(n)$
. Thus condition (4) is never again satisfied for
$\varphi _{r(p)}(n)$
. Thus condition (4) is never again satisfied for
![]() $\langle p, N \rangle $
with action input n at any stage
$\langle p, N \rangle $
with action input n at any stage
![]() $t> s$
.
$t> s$
.
Suppose that either
![]() $\varphi _{\ell (p)}(m){\uparrow }$
or
$\varphi _{\ell (p)}(m){\uparrow }$
or
![]() $\varphi _{r(p)}(m){\uparrow }$
for some m. Then no
$\varphi _{r(p)}(m){\uparrow }$
for some m. Then no
![]() $n \geq m$
can be an action input for
$n \geq m$
can be an action input for
![]() $\langle p, N \rangle $
because condition (1) always fails when
$\langle p, N \rangle $
because condition (1) always fails when
![]() $n \geq m$
. Thus only finitely many numbers n can be action inputs for
$n \geq m$
. Thus only finitely many numbers n can be action inputs for
![]() $\langle p, N \rangle $
. Because each of these n can be an action input for
$\langle p, N \rangle $
. Because each of these n can be an action input for
![]() $\langle p, N \rangle $
at most once, the pair
$\langle p, N \rangle $
at most once, the pair
![]() $\langle p, N \rangle $
demands action only finitely many times. Thus in this case,
$\langle p, N \rangle $
demands action only finitely many times. Thus in this case,
![]() $\langle p, N \rangle $
adds only finitely many elements
$\langle p, N \rangle $
adds only finitely many elements
![]() $\prec _{\mathcal {L}}$
-below z.
$\prec _{\mathcal {L}}$
-below z.
We now focus on the case in which both
![]() $\varphi _{\ell (p)}$
and
$\varphi _{\ell (p)}$
and
![]() $\varphi _{r(p)}$
are total. By cohesiveness, let
$\varphi _{r(p)}$
are total. By cohesiveness, let
![]() $(a, b) \in \{0,1\} \times \{0,1\}$
be such that
$(a, b) \in \{0,1\} \times \{0,1\}$
be such that
![]() $(\forall ^\infty n \in C)(\varphi _{\ell (p)}(n) \in A^{2p, a})$
and
$(\forall ^\infty n \in C)(\varphi _{\ell (p)}(n) \in A^{2p, a})$
and
![]() $(\forall ^\infty n \in C)(\varphi _{r(p)}(n) \in A^{2p+1, b})$
. The following Claims 1–3 establish that
$(\forall ^\infty n \in C)(\varphi _{r(p)}(n) \in A^{2p+1, b})$
. The following Claims 1–3 establish that
![]() $\langle p, N \rangle $
adds only finitely many elements
$\langle p, N \rangle $
adds only finitely many elements
![]() $\prec _{\mathcal {L}}$
-below z.
$\prec _{\mathcal {L}}$
-below z.
First, consider all pairs
![]() $\langle p, M \rangle < z$
with this fixed p.
$\langle p, M \rangle < z$
with this fixed p.
Claim 1. There is a stage
![]() $s_1 \geq s_0$
such that for every M with
$s_1 \geq s_0$
such that for every M with
![]() $\langle p, M \rangle < z$
, whenever
$\langle p, M \rangle < z$
, whenever
![]() $\langle p, M \rangle $
demands action at a stage
$\langle p, M \rangle $
demands action at a stage
![]() $s \geq s_1$
, it always has action sides
$s \geq s_1$
, it always has action sides
![]() $(a,b)$
.
$(a,b)$
.
Proof of Claim 1
There are only finitely many
![]() $\langle p, M \rangle < z$
, so it suffices to show that for each
$\langle p, M \rangle < z$
, so it suffices to show that for each
![]() $\langle p, M \rangle < z$
, there is a stage t such that
$\langle p, M \rangle < z$
, there is a stage t such that
![]() $\langle p, M \rangle $
has action sides
$\langle p, M \rangle $
has action sides
![]() $(a,b)$
whenever it demands action (if it ever demands action) after stage t.
$(a,b)$
whenever it demands action (if it ever demands action) after stage t.
Let m be the least member of C with
![]() $m \geq M$
,
$m \geq M$
,
![]() $\varphi _{\ell (p)}(m) \in A^{2p, a}$
, and
$\varphi _{\ell (p)}(m) \in A^{2p, a}$
, and
![]() $\varphi _{r(p)}(m) \in A^{2p+1, b}$
. Then whenever
$\varphi _{r(p)}(m) \in A^{2p+1, b}$
. Then whenever
![]() $\langle p, M \rangle $
demands action and the action witness
$\langle p, M \rangle $
demands action and the action witness
![]() $(a_p, b_p, n)$
has
$(a_p, b_p, n)$
has
![]() $n \geq m$
, it must be that
$n \geq m$
, it must be that
![]() $(a_p, b_p) = (a, b)$
because otherwise condition (3) would fail. Suppose, for example, that
$(a_p, b_p) = (a, b)$
because otherwise condition (3) would fail. Suppose, for example, that
![]() $\langle p, M \rangle $
demands action at stage s with action witness
$\langle p, M \rangle $
demands action at stage s with action witness
![]() $(a_p, b_p, n)$
where
$(a_p, b_p, n)$
where
![]() $n \geq m$
and
$n \geq m$
and
![]() $a_p = 1-a$
. Then
$a_p = 1-a$
. Then
![]() $M \leq m \leq n$
and
$M \leq m \leq n$
and
![]() $\varphi _{\ell (p)}(m) \in A^{2p, 1-a_p}$
, but
$\varphi _{\ell (p)}(m) \in A^{2p, 1-a_p}$
, but
![]() $m \notin W_s$
because
$m \notin W_s$
because
![]() $m \in C$
. Thus condition (3) fails, so
$m \in C$
. Thus condition (3) fails, so
![]() $\langle p, M \rangle $
could not have demanded action with action witness
$\langle p, M \rangle $
could not have demanded action with action witness
![]() $(a_p, b_p, n)$
. The assumption
$(a_p, b_p, n)$
. The assumption
![]() $b_p = 1-b$
in place of
$b_p = 1-b$
in place of
![]() $a_p = 1-a$
leads to the same contradiction. On the other hand, each
$a_p = 1-a$
leads to the same contradiction. On the other hand, each
![]() $n < m$
can be the action input for
$n < m$
can be the action input for
![]() $\langle p, M \rangle $
at most once. Therefore, there is a stage
$\langle p, M \rangle $
at most once. Therefore, there is a stage
![]() $t \geq s_0$
such that whenever
$t \geq s_0$
such that whenever
![]() $\langle p, M \rangle $
demands action at a later stage
$\langle p, M \rangle $
demands action at a later stage
![]() $s \geq t$
, the action witness must have action input
$s \geq t$
, the action witness must have action input
![]() $n \geq m$
and therefore must have action sides
$n \geq m$
and therefore must have action sides
![]() $(a, b)$
.
$(a, b)$
.
Assume that
![]() $\langle p, N \rangle $
demands action infinitely often because otherwise we can immediately conclude that it adds only finitely many elements
$\langle p, N \rangle $
demands action infinitely often because otherwise we can immediately conclude that it adds only finitely many elements
![]() $\prec _{\mathcal {L}}$
-below z. Let
$\prec _{\mathcal {L}}$
-below z. Let
![]() $s_1$
be as in Claim 1, let
$s_1$
be as in Claim 1, let
![]() $t> s_1$
be a stage at which
$t> s_1$
be a stage at which
![]() $\langle p, N \rangle $
demands action, and let
$\langle p, N \rangle $
demands action, and let
![]() $s_2 = t+1$
. Then
$s_2 = t+1$
. Then
![]() $\langle p, N \rangle $
has action sides
$\langle p, N \rangle $
has action sides
![]() $(a,b)$
at stage
$(a,b)$
at stage
![]() $t < s_2$
, and whenever some
$t < s_2$
, and whenever some
![]() $\langle p, M \rangle < z$
demands action at a stage
$\langle p, M \rangle < z$
demands action at a stage
![]() $s \geq s_2> s_1$
, it also has action sides
$s \geq s_2> s_1$
, it also has action sides
![]() $(a,b)$
. Thus at every stage
$(a,b)$
. Thus at every stage
![]() $s \geq s_2$
, the most recently used action sides by a
$s \geq s_2$
, the most recently used action sides by a
![]() $\langle p, M \rangle < z$
is always
$\langle p, M \rangle < z$
is always
![]() $(a,b)$
.
$(a,b)$
.
Claim 2. Suppose that an element k is added to
![]() $X_s$
and
$X_s$
and
![]() $k \prec _{\mathcal {L}} z$
is defined at some stage
$k \prec _{\mathcal {L}} z$
is defined at some stage
![]() $s \geq s_2$
. Then
$s \geq s_2$
. Then
![]() $k \in A^{2p, 1-a} \cap A^{2p+1, 1-b}$
.
$k \in A^{2p, 1-a} \cap A^{2p+1, 1-b}$
.
Proof of Claim 2
We already know that if
![]() $\langle q, M \rangle \geq z$
, then
$\langle q, M \rangle \geq z$
, then
![]() $\langle q, M \rangle $
does not add elements
$\langle q, M \rangle $
does not add elements
![]() $k \prec _{\mathcal {L}} z$
after stage
$k \prec _{\mathcal {L}} z$
after stage
![]() $s_2$
. Thus we need only consider pairs
$s_2$
. Thus we need only consider pairs
![]() $\langle q, M \rangle < z$
. For these pairs, we have assumed inductively that if
$\langle q, M \rangle < z$
. For these pairs, we have assumed inductively that if
![]() $\langle q, M \rangle < \langle p, N \rangle $
, then
$\langle q, M \rangle < \langle p, N \rangle $
, then
![]() $\langle q, M \rangle $
does not add elements
$\langle q, M \rangle $
does not add elements
![]() $k \prec _{\mathcal {L}} z$
after stage
$k \prec _{\mathcal {L}} z$
after stage
![]() $s_2$
. Thus we need only consider pairs
$s_2$
. Thus we need only consider pairs
![]() $\langle q, M \rangle $
with
$\langle q, M \rangle $
with
![]() $\langle p, N \rangle \leq \langle q, M \rangle < z$
. Suppose such a
$\langle p, N \rangle \leq \langle q, M \rangle < z$
. Suppose such a
![]() $\langle q, M \rangle $
acts after stage
$\langle q, M \rangle $
acts after stage
![]() $s_2$
. When
$s_2$
. When
![]() $\langle q, M \rangle $
chooses the k’s to add, it uses an
$\langle q, M \rangle $
chooses the k’s to add, it uses an
![]() $r \geq p$
in the intersection (⋆) because
$r \geq p$
in the intersection (⋆) because
![]() $\langle p, N \rangle \leq \langle q, M \rangle $
. The action of pair
$\langle p, N \rangle \leq \langle q, M \rangle $
. The action of pair
![]() $\langle q, M \rangle $
must use
$\langle q, M \rangle $
must use
![]() $(a_p, b_p) = (a,b)$
. This is because after stage
$(a_p, b_p) = (a,b)$
. This is because after stage
![]() $s_2$
,
$s_2$
,
![]() $(a,b)$
is always the most recently used action sides by the pairs of the form
$(a,b)$
is always the most recently used action sides by the pairs of the form
![]() $\langle p, K \rangle $
with
$\langle p, K \rangle $
with
![]() $\langle p, K \rangle < z$
. Because
$\langle p, K \rangle < z$
. Because
![]() $\langle p, N \rangle \leq \langle q, M \rangle < z$
, it is thus also the case that
$\langle p, N \rangle \leq \langle q, M \rangle < z$
, it is thus also the case that
![]() $(a,b)$
is always the most recently used action sides by the pairs of the form
$(a,b)$
is always the most recently used action sides by the pairs of the form
![]() $\langle p, K \rangle \leq \langle q, M \rangle $
at every stage after
$\langle p, K \rangle \leq \langle q, M \rangle $
at every stage after
![]() $s_2$
. Thus when
$s_2$
. Thus when
![]() $\langle q, M \rangle $
acts at some stage
$\langle q, M \rangle $
acts at some stage
![]() $s \geq s_2$
, it uses
$s \geq s_2$
, it uses
![]() $(a_p, b_p) = (a,b)$
, and therefore the k’s it adds to
$(a_p, b_p) = (a,b)$
, and therefore the k’s it adds to
![]() $X_s$
are chosen from
$X_s$
are chosen from
![]() $A^{2p, 1-a} \cap A^{2p+1, 1-b}$
, as claimed.
$A^{2p, 1-a} \cap A^{2p+1, 1-b}$
, as claimed.
We can now show that
![]() $\langle p, N \rangle $
adds only finitely many elements
$\langle p, N \rangle $
adds only finitely many elements
![]() $k \prec _{\mathcal {L}} z$
.
$k \prec _{\mathcal {L}} z$
.
Claim 3. The pair
![]() $\langle p, N \rangle $
adds only finitely many elements
$\langle p, N \rangle $
adds only finitely many elements
![]() $k \prec _{\mathcal {L}} z$
.
$k \prec _{\mathcal {L}} z$
.
Proof of Claim 3
Suppose that
![]() $\langle p, N \rangle $
acts at some stage
$\langle p, N \rangle $
acts at some stage
![]() $s \geq s_2$
, adds an element k to
$s \geq s_2$
, adds an element k to
![]() $X_s$
, and defines
$X_s$
, and defines
![]() $k \prec _{\mathcal {L}} z$
. Then at stage s, the action witness for
$k \prec _{\mathcal {L}} z$
. Then at stage s, the action witness for
![]() $\langle p, N \rangle $
must be
$\langle p, N \rangle $
must be
![]() $(a,b,n)$
for some n, where
$(a,b,n)$
for some n, where
![]() $\varphi _{\ell (p)}(n) = x$
for some
$\varphi _{\ell (p)}(n) = x$
for some
![]() $x \in A^{2p, a}$
,
$x \in A^{2p, a}$
,
![]() $\varphi _{r(p)}(n) = y$
for some
$\varphi _{r(p)}(n) = y$
for some
![]() $y \in A^{2p+1, b}$
, and
$y \in A^{2p+1, b}$
, and
![]() $x \prec _{\mathcal {L}} y \preceq _{\mathcal {L}} z$
. The action then places k’s of each color
$x \prec _{\mathcal {L}} y \preceq _{\mathcal {L}} z$
. The action then places k’s of each color
![]() $d \leq \max _<\{x,y\}$
in the interval
$d \leq \max _<\{x,y\}$
in the interval
![]() $(x, y)_{\mathcal {L}}$
. If
$(x, y)_{\mathcal {L}}$
. If
![]() $\langle p, N \rangle $
acts again at some later stage
$\langle p, N \rangle $
acts again at some later stage
![]() $t> s$
with some action input m, then again
$t> s$
with some action input m, then again
![]() $\varphi _{\ell (p)}(m) \in A^{2p, a}$
and
$\varphi _{\ell (p)}(m) \in A^{2p, a}$
and
![]() $\varphi _{r(p)}(m) \in A^{2p+1, b}$
. However, it cannot again be that
$\varphi _{r(p)}(m) \in A^{2p+1, b}$
. However, it cannot again be that
![]() $\varphi _{\ell (p)}(m) = x$
and
$\varphi _{\ell (p)}(m) = x$
and
![]() $\varphi _{r(p)}(m) = y$
because condition (4) would fail in this situation. Thus when adding a number
$\varphi _{r(p)}(m) = y$
because condition (4) would fail in this situation. Thus when adding a number
![]() $k \prec _{\mathcal {L}} z$
, the action input n used by
$k \prec _{\mathcal {L}} z$
, the action input n used by
![]() $\langle p, N \rangle $
specifies a pair
$\langle p, N \rangle $
specifies a pair
![]() $(x,y) = (\varphi _{\ell (p)}(n), \varphi _{r(p)}(n)) \in A^{2p, a} \times A^{2p+1, b}$
with
$(x,y) = (\varphi _{\ell (p)}(n), \varphi _{r(p)}(n)) \in A^{2p, a} \times A^{2p+1, b}$
with
![]() $x \prec _{\mathcal {L}} y \preceq _{\mathcal {L}} z$
, and each such pair can be specified by
$x \prec _{\mathcal {L}} y \preceq _{\mathcal {L}} z$
, and each such pair can be specified by
![]() $\langle p, N \rangle $
at most once. By Claim 2, every element added
$\langle p, N \rangle $
at most once. By Claim 2, every element added
![]() $\prec _{\mathcal {L}}$
-below z after stage
$\prec _{\mathcal {L}}$
-below z after stage
![]() $s_2$
is in
$s_2$
is in
![]() $A^{2p, 1-a} \cap A^{2p+1, 1-b}$
. Therefore there are only finitely many pairs
$A^{2p, 1-a} \cap A^{2p+1, 1-b}$
. Therefore there are only finitely many pairs
![]() $(x,y) \in A^{2p, a} \times A^{2p+1, b}$
with
$(x,y) \in A^{2p, a} \times A^{2p+1, b}$
with
![]() $x \prec _{\mathcal {L}} y \preceq _{\mathcal {L}} z$
, and therefore
$x \prec _{\mathcal {L}} y \preceq _{\mathcal {L}} z$
, and therefore
![]() $\langle p, N \rangle $
can only add finitely many elements
$\langle p, N \rangle $
can only add finitely many elements
![]() $k \prec _{\mathcal {L}} z$
.
$k \prec _{\mathcal {L}} z$
.
We have shown that for every z, no
![]() $\langle p, N \rangle \geq z$
adds an element
$\langle p, N \rangle \geq z$
adds an element
![]() $\prec _{\mathcal {L}}$
-below z after stage z and that each
$\prec _{\mathcal {L}}$
-below z after stage z and that each
![]() $\langle p, N \rangle < z$
adds only finitely many elements
$\langle p, N \rangle < z$
adds only finitely many elements
![]() $\prec _{\mathcal {L}}$
-below z. Thus for every z, only finitely many elements are ever added
$\prec _{\mathcal {L}}$
-below z. Thus for every z, only finitely many elements are ever added
![]() $\prec _{\mathcal {L}}$
-below z. Therefore
$\prec _{\mathcal {L}}$
-below z. Therefore
![]() $\mathcal {L} \cong \omega $
.
$\mathcal {L} \cong \omega $
.
Now let
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
be total computable functions with
$\psi $
be total computable functions with
![]() $\lim _{n \in C}\varphi (n) = \lim _{n \in C}\psi (n) = \infty $
. We complete the proof by showing that (*) is satisfied for
$\lim _{n \in C}\varphi (n) = \lim _{n \in C}\psi (n) = \infty $
. We complete the proof by showing that (*) is satisfied for
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
. Assume that
$\psi $
. Assume that
![]() $(\forall ^\infty n \in C)(\psi (n) \prec _{\mathcal {L}} \varphi (n))$
, for otherwise (*) vacuously holds. Let p be such that
$(\forall ^\infty n \in C)(\psi (n) \prec _{\mathcal {L}} \varphi (n))$
, for otherwise (*) vacuously holds. Let p be such that
![]() $\varphi _{\ell (p)} = \psi $
and
$\varphi _{\ell (p)} = \psi $
and
![]() $\varphi _{r(p)} = \varphi $
. By cohesiveness, let
$\varphi _{r(p)} = \varphi $
. By cohesiveness, let
![]() $(a,b) \in \{0,1\} \times \{0,1\}$
and
$(a,b) \in \{0,1\} \times \{0,1\}$
and
![]() $N \in \mathbb {N}$
be such that, for all
$N \in \mathbb {N}$
be such that, for all
![]() $n \in C$
with
$n \in C$
with
![]() $n> N$
,
$n> N$
,
![]() $\varphi _{\ell (p)}(n) \in A^{2p, a}$
and
$\varphi _{\ell (p)}(n) \in A^{2p, a}$
and
![]() $\varphi _{r(p)}(n) \in A^{2p+1, b}$
. Let
$\varphi _{r(p)}(n) \in A^{2p+1, b}$
. Let
![]() $n_0 \geq N$
be large enough so that for all
$n_0 \geq N$
be large enough so that for all
![]() $n \in C$
with
$n \in C$
with
![]() $n \geq n_0$
,
$n \geq n_0$
,
![]() $\varphi _{\ell (p)}(n)$
is not
$\varphi _{\ell (p)}(n)$
is not
![]() $\preceq _{\mathcal {L}}$
-below any of
$\preceq _{\mathcal {L}}$
-below any of
![]() $0, 1, \dots , \langle p, N \rangle $
. To choose
$0, 1, \dots , \langle p, N \rangle $
. To choose
![]() $n_0$
, notice that the set Z of elements that are
$n_0$
, notice that the set Z of elements that are
![]() $\preceq _{\mathcal {L}}$
-below any of
$\preceq _{\mathcal {L}}$
-below any of
![]() $0, 1, \dots , \langle p, N \rangle $
is finite because
$0, 1, \dots , \langle p, N \rangle $
is finite because
![]() $\mathcal {L} \cong \omega $
. Then
$\mathcal {L} \cong \omega $
. Then
![]() $(\forall ^\infty n \in C)(\varphi _{\ell (p)}(n) \notin Z)$
because
$(\forall ^\infty n \in C)(\varphi _{\ell (p)}(n) \notin Z)$
because
![]() $\lim _{n \in C}\varphi _{\ell (p)}(n) = \infty $
.
$\lim _{n \in C}\varphi _{\ell (p)}(n) = \infty $
.
Suppose that
![]() $n \in C$
and
$n \in C$
and
![]() $n \geq n_0$
, and furthermore suppose for a contradiction that there is a
$n \geq n_0$
, and furthermore suppose for a contradiction that there is a
![]() $d < \max _<\{\varphi _{\ell (p)}(n), \varphi _{r(p)}(n)\}$
such that there is no k with
$d < \max _<\{\varphi _{\ell (p)}(n), \varphi _{r(p)}(n)\}$
such that there is no k with
![]() $\varphi _{\ell (p)}(n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
and
$\varphi _{\ell (p)}(n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
and
![]() $F(k) = d$
. Then conditions (1)–(5) are satisfied by
$F(k) = d$
. Then conditions (1)–(5) are satisfied by
![]() $(a,b,n)$
at all sufficiently large stages s. Condition (1) is satisfied because
$(a,b,n)$
at all sufficiently large stages s. Condition (1) is satisfied because
![]() $\varphi _{\ell (p)}$
and
$\varphi _{\ell (p)}$
and
![]() $\varphi _{r(p)}$
are total. Condition (2) is satisfied because
$\varphi _{r(p)}$
are total. Condition (2) is satisfied because
![]() $n \geq N$
and
$n \geq N$
and
![]() $n \in C$
. Condition (3) is satisfied by the choice of N. Condition (4) is satisfied by the assumption that there is no k with
$n \in C$
. Condition (3) is satisfied by the choice of N. Condition (4) is satisfied by the assumption that there is no k with
![]() $\varphi _{\ell (p)}(n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
and
$\varphi _{\ell (p)}(n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
and
![]() $F(k) = d$
and hence there is no such k at every stage s at which both
$F(k) = d$
and hence there is no such k at every stage s at which both
![]() $\varphi _{\ell (p)}(n)$
and
$\varphi _{\ell (p)}(n)$
and
![]() $\varphi _{r(p)}(n)$
are present in
$\varphi _{r(p)}(n)$
are present in
![]() $X_s$
. Condition (5) is satisfied by the choice of
$X_s$
. Condition (5) is satisfied by the choice of
![]() $n_0$
. Each
$n_0$
. Each
![]() $m < n$
can be the action input for
$m < n$
can be the action input for
![]() $\langle p, N \rangle $
at most once, and, at sufficiently large stages,
$\langle p, N \rangle $
at most once, and, at sufficiently large stages,
![]() $(a,b)$
is the only possible action sides for
$(a,b)$
is the only possible action sides for
![]() $\langle p, N \rangle $
. Thus at some stage the pair
$\langle p, N \rangle $
. Thus at some stage the pair
![]() $\langle p, N \rangle $
eventually demands action with action witness
$\langle p, N \rangle $
eventually demands action with action witness
![]() $(a,b,n)$
. The action of
$(a,b,n)$
. The action of
![]() $\langle p, N \rangle $
defines
$\langle p, N \rangle $
defines
![]() $\varphi _{\ell (p)}(n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
and
$\varphi _{\ell (p)}(n) \prec _{\mathcal {L}} k \prec _{\mathcal {L}} \varphi _{r(p)}(n)$
and
![]() $F(k) = d$
for some k, which contradicts that there is no such k. This shows that (*) holds for
$F(k) = d$
for some k, which contradicts that there is no such k. This shows that (*) holds for
![]() $\varphi = \varphi _{r(p)}$
and
$\varphi = \varphi _{r(p)}$
and
![]() $\psi = \varphi _{\ell (p)}$
, which completes the proof.
$\psi = \varphi _{\ell (p)}$
, which completes the proof.
Let C be a co-c.e. cohesive set, and, by Theorem 5.3, let
![]() $\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
be a computable colored copy of
$\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
be a computable colored copy of
![]() $\omega $
for which
$\omega $
for which
![]() $\prod _C \mathcal {O}$
is colorful. Then
$\prod _C \mathcal {O}$
is colorful. Then
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
is an example of a computable copy of
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
is an example of a computable copy of
![]() $\omega $
with
$\omega $
with
![]() $\prod _C \mathcal {L} \cong \omega + \eta $
.
$\prod _C \mathcal {L} \cong \omega + \eta $
.
Corollary 5.4. Let C be a co-c.e. cohesive set. Then there is a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
where the cohesive power
$\omega $
where the cohesive power
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \eta $
.
$\omega + \eta $
.
Proof Let C be co-c.e. and cohesive. Let
![]() $\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
be the computable colored copy of
$\mathcal {O} = (L, \mathbb {N}, \prec _{\mathcal {L}}, F)$
be the computable colored copy of
![]() $\omega $
from Theorem 5.3 for C. Let
$\omega $
from Theorem 5.3 for C. Let
![]() $\mathcal {L}$
denote the computable copy
$\mathcal {L}$
denote the computable copy
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
of
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
of
![]() $\omega $
. The cohesive power
$\omega $
. The cohesive power
![]() $\prod _C \mathcal {L}$
has an initial segment of order-type
$\prod _C \mathcal {L}$
has an initial segment of order-type
![]() $\omega $
by Lemma 4.1. There is neither a least nor greatest non-standard element of
$\omega $
by Lemma 4.1. There is neither a least nor greatest non-standard element of
![]() $\prod _C \mathcal {L}$
by Lemma 4.3. Theorem 5.3 implies that the non-standard elements of
$\prod _C \mathcal {L}$
by Lemma 4.3. Theorem 5.3 implies that the non-standard elements of
![]() $\prod _C \mathcal {L}$
are dense. So
$\prod _C \mathcal {L}$
are dense. So
![]() $\prod _C \mathcal {L}$
consists of a standard part of order-type
$\prod _C \mathcal {L}$
consists of a standard part of order-type
![]() $\omega $
and a non-standard part that forms a countable dense linear order without endpoints. So
$\omega $
and a non-standard part that forms a countable dense linear order without endpoints. So
![]() $\prod _C \mathcal {L} \cong \omega + \eta $
.
$\prod _C \mathcal {L} \cong \omega + \eta $
.
Example 5.5. Let C be a co-c.e. cohesive set, and let
![]() $\mathcal {L}$
be a computable copy of
$\mathcal {L}$
be a computable copy of
![]() $\omega $
with
$\omega $
with
![]() $\prod _C \mathcal {L} \cong \omega + \eta $
as in Corollary 5.4.
$\prod _C \mathcal {L} \cong \omega + \eta $
as in Corollary 5.4.
-
(1) There is a countable collection of computable copies of
 $\omega $
whose cohesive powers over C are pairwise non-elementarily equivalent. Let
$\omega $
whose cohesive powers over C are pairwise non-elementarily equivalent. Let
 $k \geq 1$
, and let
$k \geq 1$
, and let
 $\boldsymbol {k}$
denote the k-element linear order
$\boldsymbol {k}$
denote the k-element linear order
 $0 < 1 < \cdots < k-1$
as well as its order-type. Then
$0 < 1 < \cdots < k-1$
as well as its order-type. Then
 $\boldsymbol {k}\mathcal {L}$
has order-type
$\boldsymbol {k}\mathcal {L}$
has order-type
 $\omega $
because
$\omega $
because
 $\mathcal {L}$
has order-type
$\mathcal {L}$
has order-type
 $\omega $
, and
$\omega $
, and
 $\prod _C \boldsymbol {k} \cong \boldsymbol {k}$
by the discussion following Definition 2.2. Using Theorem 3.6, we calculate The linear orders
$\prod _C \boldsymbol {k} \cong \boldsymbol {k}$
by the discussion following Definition 2.2. Using Theorem 3.6, we calculate The linear orders $$ \begin{align*} \prod\nolimits_C(\boldsymbol{k}\mathcal{L}) \;\cong\; \bigl( \prod\nolimits_C \boldsymbol{k} \bigr) \bigl( \prod\nolimits_C \mathcal{L} \bigr) \;\cong\; \boldsymbol{k}(\omega + \eta) \;\cong\; \omega + \boldsymbol{k}\eta. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C(\boldsymbol{k}\mathcal{L}) \;\cong\; \bigl( \prod\nolimits_C \boldsymbol{k} \bigr) \bigl( \prod\nolimits_C \mathcal{L} \bigr) \;\cong\; \boldsymbol{k}(\omega + \eta) \;\cong\; \omega + \boldsymbol{k}\eta. \end{align*} $$
 $\omega + \boldsymbol {k}\eta $
for
$\omega + \boldsymbol {k}\eta $
for
 $k \geq 1$
are pairwise non-elementarily equivalent. The sentence “there are
$k \geq 1$
are pairwise non-elementarily equivalent. The sentence “there are
 $x_0 \prec \cdots \prec x_{k-1}$
such that every other y satisfies either
$x_0 \prec \cdots \prec x_{k-1}$
such that every other y satisfies either
 $y \prec x_0$
or
$y \prec x_0$
or
 $x_{k-1} \prec y$
; if
$x_{k-1} \prec y$
; if
 $y \prec x_0$
, then there is a z with
$y \prec x_0$
, then there is a z with
 $y \prec z \prec x_0$
; and if
$y \prec z \prec x_0$
; and if
 $x_{k-1} \prec y$
, then there is a z with
$x_{k-1} \prec y$
, then there is a z with
 $x_{k-1} \prec z \prec y$
” expressing that there is a maximal block of size k is true of
$x_{k-1} \prec z \prec y$
” expressing that there is a maximal block of size k is true of
 $\omega + \boldsymbol {k}\eta $
, but not of
$\omega + \boldsymbol {k}\eta $
, but not of
 $\omega + \boldsymbol {m}\eta $
if
$\omega + \boldsymbol {m}\eta $
if
 $m \neq k$
. Thus
$m \neq k$
. Thus
 $\boldsymbol {1}\mathcal {L}, \boldsymbol {2}\mathcal {L}, \dots $
is a sequence of computable copies of
$\boldsymbol {1}\mathcal {L}, \boldsymbol {2}\mathcal {L}, \dots $
is a sequence of computable copies of
 $\omega $
whose cohesive powers
$\omega $
whose cohesive powers
 $\prod _C (\boldsymbol {k}\mathcal {L})$
are pairwise non-elementarily equivalent.
$\prod _C (\boldsymbol {k}\mathcal {L})$
are pairwise non-elementarily equivalent.
-
(2) It is possible for non-elementarily equivalent computable linear orders to have isomorphic cohesive powers. Consider the computable linear orders
 $\mathcal {L}$
and
$\mathcal {L}$
and
 $\mathcal {L} + \mathbb {Q}$
. They are not elementarily equivalent because the sentence “every element has an immediate successor” is true of
$\mathcal {L} + \mathbb {Q}$
. They are not elementarily equivalent because the sentence “every element has an immediate successor” is true of
 $\mathcal {L}$
but not of
$\mathcal {L}$
but not of
 $\mathcal {L} + \mathbb {Q}$
. However, using Theorem 3.6 and the fact that
$\mathcal {L} + \mathbb {Q}$
. However, using Theorem 3.6 and the fact that
 $\prod _C \mathbb {Q} \cong \eta $
, we calculate
$\prod _C \mathbb {Q} \cong \eta $
, we calculate  $$ \begin{align*} \prod\nolimits_C(\mathcal{L} + \mathbb{Q}) \;\cong\; \prod\nolimits_C \mathcal{L} + \prod\nolimits_C \mathbb{Q} \;\cong\; (\omega + \eta) + \eta \;\cong\; \omega + \eta \;\cong\; \prod\nolimits_C \mathcal{L}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C(\mathcal{L} + \mathbb{Q}) \;\cong\; \prod\nolimits_C \mathcal{L} + \prod\nolimits_C \mathbb{Q} \;\cong\; (\omega + \eta) + \eta \;\cong\; \omega + \eta \;\cong\; \prod\nolimits_C \mathcal{L}. \end{align*} $$
Thus the cohesive powers
 $\prod _C \mathcal {L}$
and
$\prod _C \mathcal {L}$
and
 $\prod _C(\mathcal {L} + \mathbb {Q})$
of
$\prod _C(\mathcal {L} + \mathbb {Q})$
of
 $\mathcal {L}$
and
$\mathcal {L}$
and
 $\mathcal {L} + \mathbb {Q}$
are isomorphic.
$\mathcal {L} + \mathbb {Q}$
are isomorphic.
6 Shuffling finite linear orders into cohesive powers of
 $\omega $
$\omega $
The goal of this section is to prove that if
![]() $X \subseteq \mathbb {N} \setminus \{0\}$
is a Boolean combination of
$X \subseteq \mathbb {N} \setminus \{0\}$
is a Boolean combination of
![]() $\Sigma _2$
sets, thought of as a set of finite order-types, and C is a co-c.e. cohesive set, then there is a computable copy
$\Sigma _2$
sets, thought of as a set of finite order-types, and C is a co-c.e. cohesive set, then there is a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
for which
$\omega $
for which
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. Here
$\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. Here
![]() $\boldsymbol {\sigma }$
denotes the shuffle operation (see Definition 6.2). We prove this in a modular way by abstracting the cohesive set away from the computable copy of
$\boldsymbol {\sigma }$
denotes the shuffle operation (see Definition 6.2). We prove this in a modular way by abstracting the cohesive set away from the computable copy of
![]() $\omega $
being constructed. The key technical step is Lemma 6.9, which states that from a computable colored copy
$\omega $
being constructed. The key technical step is Lemma 6.9, which states that from a computable colored copy
![]() $\mathcal {O}$
of
$\mathcal {O}$
of
![]() $\omega $
and a Boolean combination of
$\omega $
and a Boolean combination of
![]() $\Sigma _2$
sets
$\Sigma _2$
sets
![]() $X \subseteq \mathbb {N} \setminus \{0\}$
, we can construct a computable copy
$X \subseteq \mathbb {N} \setminus \{0\}$
, we can construct a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
such that
$\omega $
such that
![]() $\prod _C \mathcal {L} \;\cong \; \omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
whenever C is a cohesive set for which
$\prod _C \mathcal {L} \;\cong \; \omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
whenever C is a cohesive set for which
![]() $\prod _C \mathcal {O}$
is colorful. Combining Lemma 6.9 with Theorem 5.3 then gives the desired result.
$\prod _C \mathcal {O}$
is colorful. Combining Lemma 6.9 with Theorem 5.3 then gives the desired result.
Given a linear order
![]() $\mathcal {L}$
and a sequence of linear orders
$\mathcal {L}$
and a sequence of linear orders
![]() $(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
indexed by
$(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
indexed by
![]() $|\mathcal {L}|$
, the generalized sum of
$|\mathcal {L}|$
, the generalized sum of
![]() $(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
over
$(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
over
![]() $\mathcal {L}$
is obtained by replacing each element
$\mathcal {L}$
is obtained by replacing each element
![]() $\ell $
of
$\ell $
of
![]() $\mathcal {L}$
by a copy of
$\mathcal {L}$
by a copy of
![]() $\mathcal {M}_\ell $
.
$\mathcal {M}_\ell $
.
Definition 6.1 (See [Reference Rosenstein21, Definition 1.38]).
Let
![]() $\mathcal {L}$
be a linear order, and let
$\mathcal {L}$
be a linear order, and let
![]() $(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
be a sequence of linear orders indexed by
$(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
be a sequence of linear orders indexed by
![]() $|\mathcal {L}|$
. The generalized sum
$|\mathcal {L}|$
. The generalized sum
![]() $\sum _{\ell \in |\mathcal {L}|}\mathcal {M}_\ell $
of
$\sum _{\ell \in |\mathcal {L}|}\mathcal {M}_\ell $
of
![]() $(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
over
$(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
over
![]() $\mathcal {L}$
is the linear order
$\mathcal {L}$
is the linear order
![]() $\mathcal {S} = (S, \prec _{\mathcal {S}})$
defined as follows. Write
$\mathcal {S} = (S, \prec _{\mathcal {S}})$
defined as follows. Write
![]() $\mathcal {L} = (L, \prec _{\mathcal {L}})$
, and write
$\mathcal {L} = (L, \prec _{\mathcal {L}})$
, and write
![]() $\mathcal {M}_\ell = (M_\ell , \prec _{\mathcal {M}_\ell })$
for each
$\mathcal {M}_\ell = (M_\ell , \prec _{\mathcal {M}_\ell })$
for each
![]() $\ell \in L$
. Define
$\ell \in L$
. Define
![]() $S = \{(\ell , m) : \ell \in L \,\wedge \, m \in M_\ell \}$
, and define
$S = \{(\ell , m) : \ell \in L \,\wedge \, m \in M_\ell \}$
, and define
Let
![]() $\mathcal {S} = \sum _{\ell \in |\mathcal {L}|}\mathcal {M}_\ell $
be the generalized sum of a sequence of linear orders
$\mathcal {S} = \sum _{\ell \in |\mathcal {L}|}\mathcal {M}_\ell $
be the generalized sum of a sequence of linear orders
![]() $(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
over a linear order
$(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
over a linear order
![]() $\mathcal {L}$
as in Definition 6.1. Each
$\mathcal {L}$
as in Definition 6.1. Each
![]() $\mathcal {M}_\ell $
for
$\mathcal {M}_\ell $
for
![]() $\ell \in |\mathcal {L}|$
corresponds to an interval of
$\ell \in |\mathcal {L}|$
corresponds to an interval of
![]() $\mathcal {S}$
, which naturally gives rise to the sum condensation of
$\mathcal {S}$
, which naturally gives rise to the sum condensation of
![]() $\mathcal {S}$
. For
$\mathcal {S}$
. For
![]() $(\ell , m) \in |\mathcal {S}|$
, let
$(\ell , m) \in |\mathcal {S}|$
, let
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}((\ell , m)) = \{(x, y) \in |\mathcal {S}| : \ell = x\}$
. The sum condensation
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}((\ell , m)) = \{(x, y) \in |\mathcal {S}| : \ell = x\}$
. The sum condensation
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {S})$
is the condensation obtained from the partition
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {S})$
is the condensation obtained from the partition
![]() $\{\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}((\ell , m)) : (\ell , m) \in |\mathcal {S}|\}$
. Observe that
$\{\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}((\ell , m)) : (\ell , m) \in |\mathcal {S}|\}$
. Observe that
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}((\ell , m)) \cong \mathcal {M}_\ell $
for each
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}((\ell , m)) \cong \mathcal {M}_\ell $
for each
![]() $\ell \in |\mathcal {L}|$
and that
$\ell \in |\mathcal {L}|$
and that
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {S}) \cong \mathcal {L}$
.
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {S}) \cong \mathcal {L}$
.
Generalized sums generalize both the sum and product constructions of Definition 3.1. View the ordinary sum
![]() $\mathcal {L}_0 + \mathcal {L}_1$
as the generalized sum
$\mathcal {L}_0 + \mathcal {L}_1$
as the generalized sum
![]() $\sum _{\ell \in |\boldsymbol {2}|}\mathcal {L}_\ell $
of
$\sum _{\ell \in |\boldsymbol {2}|}\mathcal {L}_\ell $
of
![]() $\mathcal {L}_0$
and
$\mathcal {L}_0$
and
![]() $\mathcal {L}_1$
over the
$\mathcal {L}_1$
over the
![]() $2$
-element linear order
$2$
-element linear order
![]() $\boldsymbol {2} = (\{0,1\}, <)$
; and view the product
$\boldsymbol {2} = (\{0,1\}, <)$
; and view the product
![]() $\mathcal {L}_0 \mathcal {L}_1$
as the generalized sum
$\mathcal {L}_0 \mathcal {L}_1$
as the generalized sum
![]() $\sum _{\ell \in |\mathcal {L}_1|}\mathcal {L}_0$
of copies of
$\sum _{\ell \in |\mathcal {L}_1|}\mathcal {L}_0$
of copies of
![]() $\mathcal {L}_0$
over
$\mathcal {L}_0$
over
![]() $\mathcal {L}_1$
. We may also use generalized sums to define shuffles.
$\mathcal {L}_1$
. We may also use generalized sums to define shuffles.
The shuffle
![]() $\boldsymbol {\sigma }(X)$
of an at-most-countable non-empty collection X of linear orders is obtained by densely coloring
$\boldsymbol {\sigma }(X)$
of an at-most-countable non-empty collection X of linear orders is obtained by densely coloring
![]() $\mathbb {Q}$
with colors from X and then replacing each
$\mathbb {Q}$
with colors from X and then replacing each
![]() $q \in \mathbb {Q}$
by its color.
$q \in \mathbb {Q}$
by its color.
Definition 6.2 (See [Reference Rosenstein21, Definition 7.14]).
Let X be a non-empty collection of linear orders with
![]() $|X| \leq \aleph _0$
. Let
$|X| \leq \aleph _0$
. Let
![]() $f \colon \mathbb {Q} \rightarrow X$
be a function such that
$f \colon \mathbb {Q} \rightarrow X$
be a function such that
![]() $f^{-1}(\mathcal {M})$
is dense in
$f^{-1}(\mathcal {M})$
is dense in
![]() $\mathbb {Q}$
for each linear order
$\mathbb {Q}$
for each linear order
![]() $\mathcal {M} \in X$
. Let
$\mathcal {M} \in X$
. Let
![]() $\mathcal {S} = \sum _{q \in \mathbb {Q}} f(q)$
be the generalized sum of the sequence
$\mathcal {S} = \sum _{q \in \mathbb {Q}} f(q)$
be the generalized sum of the sequence
![]() $(f(q) : q \in \mathbb {Q})$
over
$(f(q) : q \in \mathbb {Q})$
over
![]() $\mathbb {Q}$
. By density, the order-type of
$\mathbb {Q}$
. By density, the order-type of
![]() $\mathcal {S}$
does not depend on the particular choice of f. Therefore
$\mathcal {S}$
does not depend on the particular choice of f. Therefore
![]() $\mathcal {S}$
is called the shuffle of X and is denoted
$\mathcal {S}$
is called the shuffle of X and is denoted
![]() $\boldsymbol {\sigma }(X)$
.
$\boldsymbol {\sigma }(X)$
.
We usually think of X in a shuffle
![]() $\boldsymbol {\sigma }(X)$
as a collection of order-types instead of as a collection of concrete linear orders.
$\boldsymbol {\sigma }(X)$
as a collection of order-types instead of as a collection of concrete linear orders.
Let
![]() $\mathcal {L}$
be a computable linear order, and let
$\mathcal {L}$
be a computable linear order, and let
![]() $(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
be a uniformly computable sequence of linear orders. Then one may use the pairing function to compute a copy of
$(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
be a uniformly computable sequence of linear orders. Then one may use the pairing function to compute a copy of
![]() $\sum _{\ell \in |\mathcal {L}|}\mathcal {M}_\ell $
. Likewise, if
$\sum _{\ell \in |\mathcal {L}|}\mathcal {M}_\ell $
. Likewise, if
![]() $(\mathcal {M}_n : n \in \mathbb {N})$
is a uniformly computable sequence of linear orders, then one may compute a function
$(\mathcal {M}_n : n \in \mathbb {N})$
is a uniformly computable sequence of linear orders, then one may compute a function
![]() $f \colon \mathbb {Q} \rightarrow \mathbb {N}$
such that
$f \colon \mathbb {Q} \rightarrow \mathbb {N}$
such that
![]() $f^{-1}(n)$
is dense in
$f^{-1}(n)$
is dense in
![]() $\mathbb {Q}$
for each
$\mathbb {Q}$
for each
![]() $n \in \mathbb {N}$
and thereby compute a copy of
$n \in \mathbb {N}$
and thereby compute a copy of
![]() $\boldsymbol {\sigma }(\{\mathcal {M}_n : n \in \mathbb {N}\})$
.
$\boldsymbol {\sigma }(\{\mathcal {M}_n : n \in \mathbb {N}\})$
.
Let C be co-c.e. and cohesive, let
![]() $\mathcal {L}$
be the linear order from Corollary 5.4 for C, and consider the linear order
$\mathcal {L}$
be the linear order from Corollary 5.4 for C, and consider the linear order
![]() $\boldsymbol {2}\mathcal {L}$
from Example 5.5 item (1). We can think of
$\boldsymbol {2}\mathcal {L}$
from Example 5.5 item (1). We can think of
![]() $\boldsymbol {2}\mathcal {L}$
as being obtained from
$\boldsymbol {2}\mathcal {L}$
as being obtained from
![]() $\mathcal {L}$
by replacing each element of
$\mathcal {L}$
by replacing each element of
![]() $\mathcal {L}$
by a copy of
$\mathcal {L}$
by a copy of
![]() $\boldsymbol {2}$
. This operation of replacing each element by a copy of
$\boldsymbol {2}$
. This operation of replacing each element by a copy of
![]() $\boldsymbol {2}$
is reflected in the cohesive power, and we have that
$\boldsymbol {2}$
is reflected in the cohesive power, and we have that
![]() $\prod _C (\boldsymbol {2}\mathcal {L}) \cong \omega + \boldsymbol {2}\eta $
.
$\prod _C (\boldsymbol {2}\mathcal {L}) \cong \omega + \boldsymbol {2}\eta $
.
Again let C be co-c.e. and cohesive, and now consider the computable colored copy
![]() $\mathcal {O} = (R, \mathbb {N}, \prec _{\mathcal {R}}, F)$
of
$\mathcal {O} = (R, \mathbb {N}, \prec _{\mathcal {R}}, F)$
of
![]() $\omega $
from Theorem 5.3. Let
$\omega $
from Theorem 5.3. Let
![]() $\mathcal {R}$
denote
$\mathcal {R}$
denote
![]() $(R, \prec _{\mathcal {R}})$
. Collapse F into a coloring
$(R, \prec _{\mathcal {R}})$
. Collapse F into a coloring
![]() $G \colon R \rightarrow \{0,1\}$
, where
$G \colon R \rightarrow \{0,1\}$
, where
![]() $G(r) = 0$
if
$G(r) = 0$
if
![]() $F(r) = 0$
and
$F(r) = 0$
and
![]() $G(r) = 1$
if
$G(r) = 1$
if
![]() $F(r) \geq 1$
. Then the coloring
$F(r) \geq 1$
. Then the coloring
![]() $G^{\prod _C \mathcal {O}}$
of
$G^{\prod _C \mathcal {O}}$
of
![]() $\prod _C \mathcal {R}$
induced by G uses exactly two colors:
$\prod _C \mathcal {R}$
induced by G uses exactly two colors:
![]() represented by the constant function with value
represented by the constant function with value
![]() $0$
, and
$0$
, and
![]() represented by the constant function with value
represented by the constant function with value
![]() $1$
. Both of these colors occur densely in the non-standard part of
$1$
. Both of these colors occur densely in the non-standard part of
![]() $\prod _C \mathcal {R}$
. Compute a linear order
$\prod _C \mathcal {R}$
. Compute a linear order
![]() $\mathcal {L}$
by starting with
$\mathcal {L}$
by starting with
![]() $\mathcal {R}$
, replacing each
$\mathcal {R}$
, replacing each
![]() $r \in R$
with
$r \in R$
with
![]() $G(r) = 0$
by a copy of
$G(r) = 0$
by a copy of
![]() $\boldsymbol {2}$
, and replacing each
$\boldsymbol {2}$
, and replacing each
![]() $r \in R$
with
$r \in R$
with
![]() $G(r) = 1$
by a copy of
$G(r) = 1$
by a copy of
![]() $\boldsymbol {3}$
. The cohesive power
$\boldsymbol {3}$
. The cohesive power
![]() $\prod _C \mathcal {L}$
reflects this construction, and we get the linear order obtained from
$\prod _C \mathcal {L}$
reflects this construction, and we get the linear order obtained from
![]() $\prod _C \mathcal {R}$
by replacing each point of
$\prod _C \mathcal {R}$
by replacing each point of
![]() $G^{\prod _C \mathcal {O}}$
-color
$G^{\prod _C \mathcal {O}}$
-color
![]() by a copy of
by a copy of
![]() $\boldsymbol {2}$
and replacing each point of
$\boldsymbol {2}$
and replacing each point of
![]() $G^{\prod _C \mathcal {O}}$
-color
$G^{\prod _C \mathcal {O}}$
-color
![]() by a copy of
by a copy of
![]() $\boldsymbol {3}$
. Thus we have a computable copy
$\boldsymbol {3}$
. Thus we have a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
with
$\omega $
with
![]() $\prod _C \mathcal {L} \cong \omega + \boldsymbol {\sigma }(\{\boldsymbol {2}, \boldsymbol {3}\})$
. Using this strategy, we can shuffle any finite collection of finite linear orders into a cohesive power of a computable copy of
$\prod _C \mathcal {L} \cong \omega + \boldsymbol {\sigma }(\{\boldsymbol {2}, \boldsymbol {3}\})$
. Using this strategy, we can shuffle any finite collection of finite linear orders into a cohesive power of a computable copy of
![]() $\omega $
.
$\omega $
.
To make the above argument precise and to generalize it to more complicated shuffles, we first show that cohesive powers of linear orders respect generalized sums. Let
![]() $\mathcal {L}$
be a computable linear order, and let
$\mathcal {L}$
be a computable linear order, and let
![]() $(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
be a uniformly computable sequence of linear orders indexed by
$(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
be a uniformly computable sequence of linear orders indexed by
![]() $|\mathcal {L}|$
. We wish to show that for any cohesive set C,
$|\mathcal {L}|$
. We wish to show that for any cohesive set C,
 $$ \begin{align*} \prod\nolimits_C \sum_{\ell \in |\mathcal{L}|}\mathcal{M}_\ell \quad\cong\quad \sum_{[\theta] \in \left|\prod_C \mathcal{L}\right|}\prod\nolimits_C \mathcal{M}_{\theta(n)}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \sum_{\ell \in |\mathcal{L}|}\mathcal{M}_\ell \quad\cong\quad \sum_{[\theta] \in \left|\prod_C \mathcal{L}\right|}\prod\nolimits_C \mathcal{M}_{\theta(n)}. \end{align*} $$
To do this, we must first explain what we mean by the structure
![]() $\prod _C \mathcal {M}_{\theta (n)}$
. Intuitively,
$\prod _C \mathcal {M}_{\theta (n)}$
. Intuitively,
![]() $\prod _C \mathcal {M}_{\theta (n)}$
is the cohesive product of the sequence of structures
$\prod _C \mathcal {M}_{\theta (n)}$
is the cohesive product of the sequence of structures
![]() $\mathcal {M}_{\theta (0)}, \mathcal {M}_{\theta (1)}, \mathcal {M}_{\theta (2)}, \dots $
over C, where
$\mathcal {M}_{\theta (0)}, \mathcal {M}_{\theta (1)}, \mathcal {M}_{\theta (2)}, \dots $
over C, where
![]() $\mathcal {M}_{\theta (n)}$
is undefined if
$\mathcal {M}_{\theta (n)}$
is undefined if
![]() $\theta (n){\uparrow }$
.
$\theta (n){\uparrow }$
.
Formally, let
![]() $\mathfrak {L}$
be a computable language, and let
$\mathfrak {L}$
be a computable language, and let
![]() $(\mathcal {A}_n : n \in I)$
be a uniformly computable sequence of
$(\mathcal {A}_n : n \in I)$
be a uniformly computable sequence of
![]() $\mathfrak {L}$
-structures indexed by a computable set
$\mathfrak {L}$
-structures indexed by a computable set
![]() $I \subseteq \mathbb {N}$
. Let C be a cohesive set, and let
$I \subseteq \mathbb {N}$
. Let C be a cohesive set, and let
![]() $\theta \colon \mathbb {N} \rightarrow I$
be a partial computable function with
$\theta \colon \mathbb {N} \rightarrow I$
be a partial computable function with
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
. Then
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
. Then
![]() $\prod _C \mathcal {A}_{\theta (n)}$
is defined as in Definition 2.2, except one now considers the
$\prod _C \mathcal {A}_{\theta (n)}$
is defined as in Definition 2.2, except one now considers the
![]() $=_C$
-equivalence classes of partial computable functions
$=_C$
-equivalence classes of partial computable functions
![]() $\varphi $
such that
$\varphi $
such that
![]() $\operatorname {{\mathrm {dom}}}(\varphi ) \subseteq \operatorname {{\mathrm {dom}}}(\theta )$
,
$\operatorname {{\mathrm {dom}}}(\varphi ) \subseteq \operatorname {{\mathrm {dom}}}(\theta )$
,
![]() $\forall n \, (\varphi (n){\downarrow } \,\rightarrow \, \varphi (n) \in |\mathcal {A}_{\theta (n)}|)$
, and
$\forall n \, (\varphi (n){\downarrow } \,\rightarrow \, \varphi (n) \in |\mathcal {A}_{\theta (n)}|)$
, and
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
. The results of Section 2 hold for these generalized cohesive products of the form
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
. The results of Section 2 hold for these generalized cohesive products of the form
![]() $\prod _C \mathcal {A}_{\theta (n)}$
with minor modifications to the proofs. For example, one must now consider sets of the form
$\prod _C \mathcal {A}_{\theta (n)}$
with minor modifications to the proofs. For example, one must now consider sets of the form
![]() $\bigl \{n : \mathcal {A}_{\theta (n)} \models \Phi (\varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
for various
$\bigl \{n : \mathcal {A}_{\theta (n)} \models \Phi (\varphi _0(n), \dots , \varphi _{m-1}(n))\bigr \}$
for various
![]() $\mathfrak {L}$
-formulas
$\mathfrak {L}$
-formulas
![]() $\Phi $
and partial computable functions
$\Phi $
and partial computable functions
![]() $\varphi _0, \dots , \varphi _{m-1}$
, where
$\varphi _0, \dots , \varphi _{m-1}$
, where
![]() $\mathcal {A}_{\theta (n)}$
appears in place of
$\mathcal {A}_{\theta (n)}$
appears in place of
![]() $\mathcal {A}_n$
. If
$\mathcal {A}_n$
. If
![]() $\Phi $
is uniformly decidable in
$\Phi $
is uniformly decidable in
![]() $(\mathcal {A}_n : n \in I)$
, then the preceding set remains c.e.
$(\mathcal {A}_n : n \in I)$
, then the preceding set remains c.e.
If
![]() $\theta _0, \theta _1 \colon \mathbb {N} \rightarrow I$
are two partial computable functions with
$\theta _0, \theta _1 \colon \mathbb {N} \rightarrow I$
are two partial computable functions with
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta _0)$
,
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta _0)$
,
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta _1)$
, and
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta _1)$
, and
![]() $\theta _0 =_C \theta _1$
, then it is straightforward to show that
$\theta _0 =_C \theta _1$
, then it is straightforward to show that
![]() $\prod _C \mathcal {A}_{\theta _0(n)} \cong \prod _C \mathcal {A}_{\theta _1(n)}$
. In fact, we are even justified in writing
$\prod _C \mathcal {A}_{\theta _0(n)} \cong \prod _C \mathcal {A}_{\theta _1(n)}$
. In fact, we are even justified in writing
![]() $\prod _C \mathcal {A}_{\theta _0(n)} = \prod _C \mathcal {A}_{\theta _1(n)}$
because every element of either structure can be represented by a partial computable
$\prod _C \mathcal {A}_{\theta _0(n)} = \prod _C \mathcal {A}_{\theta _1(n)}$
because every element of either structure can be represented by a partial computable
![]() $\varphi $
with
$\varphi $
with
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi ) \subseteq \operatorname {{\mathrm {dom}}}(\theta _0) \cap \operatorname {{\mathrm {dom}}}(\theta _1)$
. In particular, the structure
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi ) \subseteq \operatorname {{\mathrm {dom}}}(\theta _0) \cap \operatorname {{\mathrm {dom}}}(\theta _1)$
. In particular, the structure
![]() $\sum _{[\theta ] \in \left |\prod _C \mathcal {L}\right |}\prod _C \mathcal {M}_{\theta (n)}$
above is well-defined.
$\sum _{[\theta ] \in \left |\prod _C \mathcal {L}\right |}\prod _C \mathcal {M}_{\theta (n)}$
above is well-defined.
Lastly, we point out that if C is a co-c.e. cohesive set with
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
, then the generalized cohesive product
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
, then the generalized cohesive product
![]() $\prod _C \mathcal {A}_{\theta (n)}$
can be realized as a cohesive product of the form
$\prod _C \mathcal {A}_{\theta (n)}$
can be realized as a cohesive product of the form
![]() $\prod _C \mathcal {B}_n$
. The argument is similar to the argument that every element of a cohesive product by a co-c.e. cohesive set has a total computable representative. Fix any computable
$\prod _C \mathcal {B}_n$
. The argument is similar to the argument that every element of a cohesive product by a co-c.e. cohesive set has a total computable representative. Fix any computable
![]() $\mathfrak {L}$
-structure
$\mathfrak {L}$
-structure
![]() $\mathcal {D}$
. Let N be such that
$\mathcal {D}$
. Let N be such that
![]() $(\forall n> N)(n \in C \rightarrow \theta (n){\downarrow })$
. Define the uniformly computable sequence of
$(\forall n> N)(n \in C \rightarrow \theta (n){\downarrow })$
. Define the uniformly computable sequence of
![]() $\mathfrak {L}$
-structures
$\mathfrak {L}$
-structures
![]() $(\mathcal {B}_n : n \in \mathbb {N})$
by
$(\mathcal {B}_n : n \in \mathbb {N})$
by
 $$ \begin{align*} \mathcal{B}_n = \begin{cases} \mathcal{A}_{\theta(n)}, & \text{if }n> N\text{ and }\theta(n){\downarrow}\text{ before }n\text{ is enumerated into }\overline{C},\\ \mathcal{D}, & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{B}_n = \begin{cases} \mathcal{A}_{\theta(n)}, & \text{if }n> N\text{ and }\theta(n){\downarrow}\text{ before }n\text{ is enumerated into }\overline{C},\\ \mathcal{D}, & \text{otherwise}. \end{cases} \end{align*} $$
Then
![]() $\prod _C \mathcal {B}_n \cong \prod _C \mathcal {A}_{\theta (n)}$
. Again, we may even write
$\prod _C \mathcal {B}_n \cong \prod _C \mathcal {A}_{\theta (n)}$
. Again, we may even write
![]() $\prod _C \mathcal {B}_n = \prod _C \mathcal {A}_{\theta (n)}$
because every element of either structure can be represented by a partial computable
$\prod _C \mathcal {B}_n = \prod _C \mathcal {A}_{\theta (n)}$
because every element of either structure can be represented by a partial computable
![]() $\varphi $
with
$\varphi $
with
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi ) \subseteq \operatorname {{\mathrm {dom}}}(\theta )$
.
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi ) \subseteq \operatorname {{\mathrm {dom}}}(\theta )$
.
We are now prepared to show that the cohesive power of a generalized sum is a generalized sum of cohesive products in the way indicated above. The method of Theorem 3.6 becomes unwieldy in this situation because of the infinite sequence of structures to juggle, so we opt for a more hands-on proof.
Theorem 6.3. Let
![]() $\mathcal {L}$
be a computable linear order, and let
$\mathcal {L}$
be a computable linear order, and let
![]() $(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
be a uniformly computable sequence of linear orders indexed by
$(\mathcal {M}_\ell : \ell \in |\mathcal {L}|)$
be a uniformly computable sequence of linear orders indexed by
![]() $|\mathcal {L}|$
. Let C be a cohesive set. Then
$|\mathcal {L}|$
. Let C be a cohesive set. Then
 $$ \begin{align*} \prod\nolimits_C \sum_{\ell \in |\mathcal{L}|}\mathcal{M}_\ell \quad\cong\quad \sum_{[\theta] \in \left|\prod_C \mathcal{L}\right|}\prod\nolimits_C \mathcal{M}_{\theta(n)}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \sum_{\ell \in |\mathcal{L}|}\mathcal{M}_\ell \quad\cong\quad \sum_{[\theta] \in \left|\prod_C \mathcal{L}\right|}\prod\nolimits_C \mathcal{M}_{\theta(n)}. \end{align*} $$
Proof To ease notation, let
 $$ \begin{align*} \mathcal{M} &= \sum_{\ell \in |\mathcal{L}|}\mathcal{M}_\ell,\\ \mathcal{X} &= \prod\nolimits_C \mathcal{L}, \\ \mathcal{Y}_{[\theta]_{\mathcal{X}}} &= \prod\nolimits_C \mathcal{M}_{\theta(n)} \quad\text{for each }[\theta]_{\mathcal{X}} \in |\mathcal{X}|,\\ \mathcal{A} &= \prod\nolimits_C \mathcal{M}, \\ \mathcal{B} &= \sum_{[\theta]_{\mathcal{X}} \in |\mathcal{X}|} \mathcal{Y}_{[\theta]_{\mathcal{X}}}. \end{align*} $$
$$ \begin{align*} \mathcal{M} &= \sum_{\ell \in |\mathcal{L}|}\mathcal{M}_\ell,\\ \mathcal{X} &= \prod\nolimits_C \mathcal{L}, \\ \mathcal{Y}_{[\theta]_{\mathcal{X}}} &= \prod\nolimits_C \mathcal{M}_{\theta(n)} \quad\text{for each }[\theta]_{\mathcal{X}} \in |\mathcal{X}|,\\ \mathcal{A} &= \prod\nolimits_C \mathcal{M}, \\ \mathcal{B} &= \sum_{[\theta]_{\mathcal{X}} \in |\mathcal{X}|} \mathcal{Y}_{[\theta]_{\mathcal{X}}}. \end{align*} $$
The goal is to show that
![]() $\mathcal {A} \cong \mathcal {B}$
. The elements of
$\mathcal {A} \cong \mathcal {B}$
. The elements of
![]() $\mathcal {A}$
are of the form
$\mathcal {A}$
are of the form
![]() $[\varphi ]_{\mathcal {A}}$
for partial computable functions
$[\varphi ]_{\mathcal {A}}$
for partial computable functions
![]() $\varphi $
with
$\varphi $
with
![]() $\forall n \, (\varphi (n){\downarrow } \,\rightarrow \, \varphi (n) \in |\mathcal {M}|)$
and
$\forall n \, (\varphi (n){\downarrow } \,\rightarrow \, \varphi (n) \in |\mathcal {M}|)$
and
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
. The elements of
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
. The elements of
![]() $\mathcal {B}$
are of the form
$\mathcal {B}$
are of the form
![]() $\bigl ([\theta ]_{\mathcal {X}}, [\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}}\bigr )$
for partial computable functions
$\bigl ([\theta ]_{\mathcal {X}}, [\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}}\bigr )$
for partial computable functions
![]() $\theta $
and
$\theta $
and
![]() $\tau $
with
$\tau $
with
![]() $\forall n \, (\theta (n){\downarrow } \,\rightarrow \, \theta (n) \in |\mathcal {L}|)$
,
$\forall n \, (\theta (n){\downarrow } \,\rightarrow \, \theta (n) \in |\mathcal {L}|)$
,
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
,
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
,
![]() $\operatorname {{\mathrm {dom}}}(\tau ) \subseteq \operatorname {{\mathrm {dom}}}(\theta )$
,
$\operatorname {{\mathrm {dom}}}(\tau ) \subseteq \operatorname {{\mathrm {dom}}}(\theta )$
,
![]() $\forall n \, (\tau (n){\downarrow } \,\rightarrow \, \tau (n) \in |\mathcal {M}_{\theta (n)}|)$
, and
$\forall n \, (\tau (n){\downarrow } \,\rightarrow \, \tau (n) \in |\mathcal {M}_{\theta (n)}|)$
, and
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\tau )$
.
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\tau )$
.
Define a function
![]() $F \colon |\mathcal {A}| \rightarrow |\mathcal {B}|$
as follows. For
$F \colon |\mathcal {A}| \rightarrow |\mathcal {B}|$
as follows. For
![]() $[\varphi ]_{\mathcal {A}} \in |\mathcal {A}|$
, we have that
$[\varphi ]_{\mathcal {A}} \in |\mathcal {A}|$
, we have that
![]() $\varphi (n) \in |\mathcal {M}|$
and therefore that
$\varphi (n) \in |\mathcal {M}|$
and therefore that
![]() $\varphi (n) = \langle \ell , m \rangle $
for some
$\varphi (n) = \langle \ell , m \rangle $
for some
![]() $\ell \in |\mathcal {L}|$
and
$\ell \in |\mathcal {L}|$
and
![]() $m \in | \mathcal {M}_\ell |$
whenever
$m \in | \mathcal {M}_\ell |$
whenever
![]() $\varphi (n){\downarrow }$
. Let
$\varphi (n){\downarrow }$
. Let
![]() $\theta = \pi _0 \circ \varphi $
, and let
$\theta = \pi _0 \circ \varphi $
, and let
![]() $\tau = \pi _1 \circ \varphi $
. Then
$\tau = \pi _1 \circ \varphi $
. Then
![]() $[\theta ]_{\mathcal {X}} \in |\mathcal {X}|$
and
$[\theta ]_{\mathcal {X}} \in |\mathcal {X}|$
and
![]() $[\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}} \in \mathcal {Y}_{[\theta ]_{\mathcal {X}}}$
. Set
$[\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}} \in \mathcal {Y}_{[\theta ]_{\mathcal {X}}}$
. Set
![]() $F([\varphi ]_{\mathcal {A}}) = \bigl ([\theta ]_{\mathcal {X}}, [\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}}\bigr )$
. To see that F is well-defined, observe that if
$F([\varphi ]_{\mathcal {A}}) = \bigl ([\theta ]_{\mathcal {X}}, [\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}}\bigr )$
. To see that F is well-defined, observe that if
![]() $\varphi =_C \psi $
, then also
$\varphi =_C \psi $
, then also
![]() $\pi _0 \circ \varphi =_C \pi _0 \circ \psi $
and
$\pi _0 \circ \varphi =_C \pi _0 \circ \psi $
and
![]() $\pi _1 \circ \varphi =_C \pi _1 \circ \psi $
.
$\pi _1 \circ \varphi =_C \pi _1 \circ \psi $
.
To show that F is an isomorphism, it suffices to show that F is surjective and order-preserving by Lemma 3.5.
For surjectivity, consider an element
![]() $\bigl ([\theta ]_{\mathcal {X}}, [\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}}\bigr )$
of
$\bigl ([\theta ]_{\mathcal {X}}, [\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}}\bigr )$
of
![]() $\mathcal {B}$
. Define a partial computable
$\mathcal {B}$
. Define a partial computable
![]() $\varphi $
by
$\varphi $
by
![]() $\varphi (n) \simeq \langle \theta (n), \tau (n) \rangle $
. Then
$\varphi (n) \simeq \langle \theta (n), \tau (n) \rangle $
. Then
![]() $\varphi (n) \in |\mathcal {M}|$
whenever
$\varphi (n) \in |\mathcal {M}|$
whenever
![]() $\varphi (n){\downarrow }$
, and
$\varphi (n){\downarrow }$
, and
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
because
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\varphi )$
because
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta ) \cap \operatorname {{\mathrm {dom}}}(\tau )$
. It follows that
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta ) \cap \operatorname {{\mathrm {dom}}}(\tau )$
. It follows that
![]() $[\varphi ]_{\mathcal {A}} \in |\mathcal {A}|$
and
$[\varphi ]_{\mathcal {A}} \in |\mathcal {A}|$
and
![]() $F([\varphi ]_{\mathcal {A}}) = \bigl ([\theta ]_{\mathcal {X}}, [\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}}\bigr )$
.
$F([\varphi ]_{\mathcal {A}}) = \bigl ([\theta ]_{\mathcal {X}}, [\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}}\bigr )$
.
For order-preserving, suppose that
![]() $[\varphi ]_{\mathcal {A}}$
and
$[\varphi ]_{\mathcal {A}}$
and
![]() $[\psi ]_{\mathcal {A}}$
are members of
$[\psi ]_{\mathcal {A}}$
are members of
![]() $\mathcal {A}$
with
$\mathcal {A}$
with
![]() $[\varphi ]_{\mathcal {A}} \prec _{\mathcal {A}} [\psi ]_{\mathcal {A}}$
. Then
$[\varphi ]_{\mathcal {A}} \prec _{\mathcal {A}} [\psi ]_{\mathcal {A}}$
. Then
![]() $(\forall ^\infty n \in C)(\varphi (n) \prec _{\mathcal {M}} \psi (n))$
. Write
$(\forall ^\infty n \in C)(\varphi (n) \prec _{\mathcal {M}} \psi (n))$
. Write
![]() $\theta = \pi _0 \circ \varphi $
,
$\theta = \pi _0 \circ \varphi $
,
![]() $\tau = \pi _1 \circ \varphi $
,
$\tau = \pi _1 \circ \varphi $
,
![]() $\alpha = \pi _0 \circ \psi $
, and
$\alpha = \pi _0 \circ \psi $
, and
![]() $\beta = \pi _1 \circ \psi $
. By the definition of
$\beta = \pi _1 \circ \psi $
. By the definition of
![]() $\mathcal {M}$
,
$\mathcal {M}$
,
Thus by cohesiveness, either:
-
•
 $(\forall ^\infty n \in C)\bigl ( \theta (n) \prec _{\mathcal {L}} \alpha (n) \bigr )$
or
$(\forall ^\infty n \in C)\bigl ( \theta (n) \prec _{\mathcal {L}} \alpha (n) \bigr )$
or -
•
 $(\forall ^\infty n \in C)\bigl ( \theta (n) = \alpha (n) \,\wedge \, \tau (n) \prec _{\mathcal {M}_{\theta (n)}} \beta (n) \bigr )$
.
$(\forall ^\infty n \in C)\bigl ( \theta (n) = \alpha (n) \,\wedge \, \tau (n) \prec _{\mathcal {M}_{\theta (n)}} \beta (n) \bigr )$
.
In the first case,
![]() $[\theta ]_{\mathcal {X}} \prec _{\mathcal {X}} [\alpha ]_{\mathcal {X}}$
. In the second case,
$[\theta ]_{\mathcal {X}} \prec _{\mathcal {X}} [\alpha ]_{\mathcal {X}}$
. In the second case,
![]() $[\theta ]_{\mathcal {X}} = [\alpha ]_{\mathcal {X}}$
and
$[\theta ]_{\mathcal {X}} = [\alpha ]_{\mathcal {X}}$
and
![]() $[\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}} \prec _{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}} [\beta ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}}$
. Thus in either case,
$[\tau ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}} \prec _{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}} [\beta ]_{\mathcal {Y}_{[\theta ]_{\mathcal {X}}}}$
. Thus in either case,
as desired.
Notice that Theorem 3.6 items (1) and (2) follow from Theorem 6.3 by viewing ordinary sums and products of linear orders as generalized sums of linear orders.
We now show how to shuffle finitely many finite order-types into the cohesive power of a computable copy of
![]() $\omega $
.
$\omega $
.
Lemma 6.4. Let
![]() $(\mathcal {M}_n : n \in I)$
be a uniformly computable sequence of linear orders indexed by a computable
$(\mathcal {M}_n : n \in I)$
be a uniformly computable sequence of linear orders indexed by a computable
![]() $I \subseteq \mathbb {N}$
, and let
$I \subseteq \mathbb {N}$
, and let
![]() $M_n$
denote the domain of
$M_n$
denote the domain of
![]() $\mathcal {M}_n$
for each
$\mathcal {M}_n$
for each
![]() $n \in I$
. Let C be a cohesive set. Let
$n \in I$
. Let C be a cohesive set. Let
![]() $\theta \colon \mathbb {N} \rightarrow I$
be a partial computable function with
$\theta \colon \mathbb {N} \rightarrow I$
be a partial computable function with
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
. Suppose that there is a
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
. Suppose that there is a
![]() $k> 0$
such that
$k> 0$
such that
![]() $(\forall ^\infty n \in C)(|M_{\theta (n)}| = k)$
. Then
$(\forall ^\infty n \in C)(|M_{\theta (n)}| = k)$
. Then
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
.
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
.
Proof As explained at the beginning of Section 2, the property “there are exactly k distinct elements” can be expressed by a
![]() $\Delta _2$
sentence
$\Delta _2$
sentence
![]() $\Phi $
. We have that
$\Phi $
. We have that
![]() $C \subseteq ^* \{n : \mathcal {M}_{\theta (n)} \models \Phi \}$
by assumption. Therefore
$C \subseteq ^* \{n : \mathcal {M}_{\theta (n)} \models \Phi \}$
by assumption. Therefore
![]() $\prod _C \mathcal {M}_{\theta (n)} \models \Phi $
by Theorem 2.7 item (3). Thus
$\prod _C \mathcal {M}_{\theta (n)} \models \Phi $
by Theorem 2.7 item (3). Thus
![]() $\prod _C \mathcal {M}_{\theta (n)}$
is a linear order with exactly k elements. So
$\prod _C \mathcal {M}_{\theta (n)}$
is a linear order with exactly k elements. So
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
.
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
.
Lemma 6.5. Let
![]() $k_0, \dots , k_N$
be non-zero natural numbers, and let
$k_0, \dots , k_N$
be non-zero natural numbers, and let
![]() $\mathcal {O}$
be a computable colored copy of
$\mathcal {O}$
be a computable colored copy of
![]() $\omega $
. There is a computable copy
$\omega $
. There is a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
(constructed from
$\omega $
(constructed from
![]() $\mathcal {O}$
) such that for every cohesive set C, if
$\mathcal {O}$
) such that for every cohesive set C, if
![]() $\prod _C \mathcal {O}$
is colorful, then
$\prod _C \mathcal {O}$
is colorful, then
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \boldsymbol {\sigma }(\{\boldsymbol {k}_0, \dots , \boldsymbol {k}_N\})$
.
$\omega + \boldsymbol {\sigma }(\{\boldsymbol {k}_0, \dots , \boldsymbol {k}_N\})$
.
Proof Let
![]() $\mathcal {O} = (R, \mathbb {N}, \prec _{\mathcal {R}}, F)$
be a computable colored copy of
$\mathcal {O} = (R, \mathbb {N}, \prec _{\mathcal {R}}, F)$
be a computable colored copy of
![]() $\omega $
, and let
$\omega $
, and let
![]() $\mathcal {R}$
denote
$\mathcal {R}$
denote
![]() $(R, \prec _{\mathcal {R}})$
. For
$(R, \prec _{\mathcal {R}})$
. For
![]() $k> 0$
, let
$k> 0$
, let
![]() $\boldsymbol {k} = (\{0, 1, \dots , k-1\}, <)$
denote the usual presentation of the k-element linear order. Let
$\boldsymbol {k} = (\{0, 1, \dots , k-1\}, <)$
denote the usual presentation of the k-element linear order. Let
![]() $(\mathcal {M}_r : r \in R)$
be the uniformly computable sequence of linear orders where
$(\mathcal {M}_r : r \in R)$
be the uniformly computable sequence of linear orders where
![]() $\mathcal {M}_r = \boldsymbol {k}_{F(r)}$
if
$\mathcal {M}_r = \boldsymbol {k}_{F(r)}$
if
![]() $F(r) < N$
and
$F(r) < N$
and
![]() $\mathcal {M}_r = \boldsymbol {k}_N$
if
$\mathcal {M}_r = \boldsymbol {k}_N$
if
![]() $F(r) \geq N$
. Let
$F(r) \geq N$
. Let
![]() $\mathcal {L}$
be the generalized sum
$\mathcal {L}$
be the generalized sum
![]() $\mathcal {L} = \sum _{r \in R} \mathcal {M}_r$
. The linear order
$\mathcal {L} = \sum _{r \in R} \mathcal {M}_r$
. The linear order
![]() $\mathcal {L}$
is obtained from the copy
$\mathcal {L}$
is obtained from the copy
![]() $\mathcal {R}$
of
$\mathcal {R}$
of
![]() $\omega $
by replacing each element of
$\omega $
by replacing each element of
![]() $\mathcal {R}$
by a finite linear order. Thus
$\mathcal {R}$
by a finite linear order. Thus
![]() $\mathcal {L}$
is infinite, and every element has only finitely many predecessors. So
$\mathcal {L}$
is infinite, and every element has only finitely many predecessors. So
![]() $\mathcal {L}$
is a computable copy of
$\mathcal {L}$
is a computable copy of
![]() $\omega $
.
$\omega $
.
Let C be a cohesive set for which
![]() $\prod _C \mathcal {O}$
is colorful. We need to show that
$\prod _C \mathcal {O}$
is colorful. We need to show that
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \boldsymbol {\sigma }(\{\boldsymbol {k}_0, \dots , \boldsymbol {k}_N\})$
.
$\omega + \boldsymbol {\sigma }(\{\boldsymbol {k}_0, \dots , \boldsymbol {k}_N\})$
.
By Theorem 6.3,
 $$ \begin{align*} \prod\nolimits_C \mathcal{L} \quad=\quad \prod\nolimits_C \sum_{r \in R}\mathcal{M}_r \quad\cong\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|}\prod\nolimits_C \mathcal{M}_{\theta(n)}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathcal{L} \quad=\quad \prod\nolimits_C \sum_{r \in R}\mathcal{M}_r \quad\cong\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|}\prod\nolimits_C \mathcal{M}_{\theta(n)}. \end{align*} $$
To ease notation, let
![]() $\mathcal {Z}$
denote the linear order
$\mathcal {Z}$
denote the linear order
![]() $\sum _{[\theta ] \in \left |\prod _C \mathcal {R}\right |}\prod _C \mathcal {M}_{\theta (n)}$
. Let
$\sum _{[\theta ] \in \left |\prod _C \mathcal {R}\right |}\prod _C \mathcal {M}_{\theta (n)}$
. Let
![]() $|\prod _C \mathcal {R}|_{\mathrm {std}}$
and
$|\prod _C \mathcal {R}|_{\mathrm {std}}$
and
![]() $|\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
denote the standard and non-standard parts of
$|\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
denote the standard and non-standard parts of
![]() $\prod _C \mathcal {R}$
, respectively. Then let
$\prod _C \mathcal {R}$
, respectively. Then let
 $$ \begin{align*} \mathcal{Z}_{\mathrm{std}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{std}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \\ \mathcal{Z}_{\mathrm{nonstd}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{nonstd}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \end{align*} $$
$$ \begin{align*} \mathcal{Z}_{\mathrm{std}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{std}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \\ \mathcal{Z}_{\mathrm{nonstd}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{nonstd}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \end{align*} $$
so that
![]() $\mathcal {Z} \cong \mathcal {Z}_{\mathrm {std}} + \mathcal {Z}_{\mathrm {nonstd}}$
. Consider the sum condensation
$\mathcal {Z} \cong \mathcal {Z}_{\mathrm {std}} + \mathcal {Z}_{\mathrm {nonstd}}$
. Consider the sum condensation
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z})$
of
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z})$
of
![]() $\mathcal {Z}$
. We show that the order-type of the block
$\mathcal {Z}$
. We show that the order-type of the block
![]() $\prod _C \mathcal {M}_{\theta (n)}$
of the sum condensation corresponding to
$\prod _C \mathcal {M}_{\theta (n)}$
of the sum condensation corresponding to
![]() $[\theta ] \in |\prod _C \mathcal {R}|$
is determined by the color
$[\theta ] \in |\prod _C \mathcal {R}|$
is determined by the color
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
of
$F^{\prod _C \mathcal {O}}([\theta ])$
of
![]() $[\theta ]$
in
$[\theta ]$
in
![]() $\prod _C \mathcal {O}$
.
$\prod _C \mathcal {O}$
.
Claim 1. If
![]() $[\theta ] \in |\prod _C \mathcal {R}|$
and
$[\theta ] \in |\prod _C \mathcal {R}|$
and
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
is solid color
$F^{\prod _C \mathcal {O}}([\theta ])$
is solid color
![]() for an
for an
![]() $i < N$
, then
$i < N$
, then
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_i$
.
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_i$
.
Proof of Claim 1
That
![]() means that
means that
![]() $(\forall ^\infty n \in C)(F(\theta (n)) = i)$
. Therefore
$(\forall ^\infty n \in C)(F(\theta (n)) = i)$
. Therefore
![]() $\mathcal {M}_{\theta (n)} = \boldsymbol {k}_{F(\theta (n))} = \boldsymbol {k}_i$
for almost every
$\mathcal {M}_{\theta (n)} = \boldsymbol {k}_{F(\theta (n))} = \boldsymbol {k}_i$
for almost every
![]() $n \in C$
because
$n \in C$
because
![]() $i < N$
. Thus
$i < N$
. Thus
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_i$
by Lemma 6.4.
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_i$
by Lemma 6.4.
Claim 2. If
![]() $[\theta ] \in |\prod _C \mathcal {R}|$
and either
$[\theta ] \in |\prod _C \mathcal {R}|$
and either
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
is solid color
$F^{\prod _C \mathcal {O}}([\theta ])$
is solid color
![]() for an
for an
![]() $i \geq N$
or
$i \geq N$
or
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
is a striped color, then
$F^{\prod _C \mathcal {O}}([\theta ])$
is a striped color, then
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_N$
.
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_N$
.
Proof of Claim 2
If
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
is a striped color, then
$F^{\prod _C \mathcal {O}}([\theta ])$
is a striped color, then
![]() $\lim _{n \in C} F(\theta (n)) = \infty $
. Therefore
$\lim _{n \in C} F(\theta (n)) = \infty $
. Therefore
![]() $(\forall ^\infty n \in C)(F(\theta (n)) \geq N)$
in both cases, so
$(\forall ^\infty n \in C)(F(\theta (n)) \geq N)$
in both cases, so
![]() $\mathcal {M}_{\theta (n)} = \boldsymbol {k}_N$
for almost every
$\mathcal {M}_{\theta (n)} = \boldsymbol {k}_N$
for almost every
![]() $n \in C$
. Thus
$n \in C$
. Thus
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_N$
by Lemma 6.4.
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_N$
by Lemma 6.4.
Notice that block
![]() $\prod _C \mathcal {M}_{\theta (n)}$
is a finite linear order for every
$\prod _C \mathcal {M}_{\theta (n)}$
is a finite linear order for every
![]() $[\theta ] \in |\prod _C \mathcal {R}|$
. Thus
$[\theta ] \in |\prod _C \mathcal {R}|$
. Thus
![]() $\mathcal {Z}_{\mathrm {std}}$
is a generalized sum of finite linear orders over the copy
$\mathcal {Z}_{\mathrm {std}}$
is a generalized sum of finite linear orders over the copy
![]() $|\prod _C \mathcal {R}|_{\mathrm {std}}$
of
$|\prod _C \mathcal {R}|_{\mathrm {std}}$
of
![]() $\omega $
, so
$\omega $
, so
![]() $\mathcal {Z}_{\mathrm {std}} \cong \omega $
.
$\mathcal {Z}_{\mathrm {std}} \cong \omega $
.
Think of the sum condensation
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}})$
as being colored by
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}})$
as being colored by
![]() $F^{\prod _C \mathcal {O}}$
, where the block
$F^{\prod _C \mathcal {O}}$
, where the block
![]() $\prod _C \mathcal {M}_{\theta (n)}$
corresponding to
$\prod _C \mathcal {M}_{\theta (n)}$
corresponding to
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
gets color
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
gets color
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
. The product
$F^{\prod _C \mathcal {O}}([\theta ])$
. The product
![]() $\prod _C \mathcal {O}$
is colorful, which means that
$\prod _C \mathcal {O}$
is colorful, which means that
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}}) \cong |\prod _C \mathcal {R}|_{\mathrm {nonstd}} \cong \eta $
and that each solid color occurs densely. By Claims 1 and 2, the order-type of block
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}}) \cong |\prod _C \mathcal {R}|_{\mathrm {nonstd}} \cong \eta $
and that each solid color occurs densely. By Claims 1 and 2, the order-type of block
![]() $\prod _C \mathcal {M}_{\theta (n)}$
for
$\prod _C \mathcal {M}_{\theta (n)}$
for
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
is:
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
is:
-
•
 $\boldsymbol {k}_i$
if
$\boldsymbol {k}_i$
if
 $[\theta ]$
has solid color
$[\theta ]$
has solid color
 for an
for an
 $i < N$
.
$i < N$
. -
•
 $\boldsymbol {k}_N$
if
$\boldsymbol {k}_N$
if
 $[\theta ]$
has either solid color
$[\theta ]$
has either solid color
 for an
for an
 $i \geq N$
or a striped color.
$i \geq N$
or a striped color.
Therefore
![]() $\mathcal {Z}_{\mathrm {nonstd}} \;\cong \; \boldsymbol {\sigma }(\{\boldsymbol {k}_0, \dots , \boldsymbol {k}_N\})$
. Thus
$\mathcal {Z}_{\mathrm {nonstd}} \;\cong \; \boldsymbol {\sigma }(\{\boldsymbol {k}_0, \dots , \boldsymbol {k}_N\})$
. Thus
as desired.
To handle more complicated patterns of shuffles, we consider sequences of finite linear orders in which we know the successor relation, we know the least element, we do not necessarily know the greatest element, but we do know that there are at most three elements that the greatest element could be. Expand the language of linear orders to
![]() $\mathfrak {O} = \{\prec , S, B, T_0, T_1, T_2\}$
, where S is a binary relation symbol and B,
$\mathfrak {O} = \{\prec , S, B, T_0, T_1, T_2\}$
, where S is a binary relation symbol and B,
![]() $T_0$
,
$T_0$
,
![]() $T_1$
, and
$T_1$
, and
![]() $T_2$
are unary relation symbols. Our intent is to describe finite linear orders with immediate successor relation S, least element given by B, and greatest element given by either
$T_2$
are unary relation symbols. Our intent is to describe finite linear orders with immediate successor relation S, least element given by B, and greatest element given by either
![]() $T_0$
,
$T_0$
,
![]() $T_1$
, or
$T_1$
, or
![]() $T_2$
. Thus S stands for “successor,” B stands for “bottom,” and T stands for “top.”
$T_2$
. Thus S stands for “successor,” B stands for “bottom,” and T stands for “top.”
Let
![]() $\Gamma $
be the set of
$\Gamma $
be the set of
![]() $\mathfrak {O}$
-sentences consisting of the linear order axioms from the beginning of Section 3 along with the following sentences.
$\mathfrak {O}$
-sentences consisting of the linear order axioms from the beginning of Section 3 along with the following sentences.
-
•
 $\forall x \forall y \, (S(x,y) \;\leftrightarrow \; y\text { is the }\prec \text {-immediate successor of }x)$
I.e.,
$\forall x \forall y \, (S(x,y) \;\leftrightarrow \; y\text { is the }\prec \text {-immediate successor of }x)$
I.e.,
 $S(x,y)$
describes the immediate successor relation.
$S(x,y)$
describes the immediate successor relation. -
•
 $\forall x \, (\exists y \, (x \prec y) \;\rightarrow \; \exists y \, S(x,y))$
I.e., every element except the last element has an immediate successor.
$\forall x \, (\exists y \, (x \prec y) \;\rightarrow \; \exists y \, S(x,y))$
I.e., every element except the last element has an immediate successor. -
•
 $\forall x \, (\exists y \, (y \prec x) \,\rightarrow \, \exists y \, S(y,x))$
I.e., every element except the first element has an immediate predecessor.
$\forall x \, (\exists y \, (y \prec x) \,\rightarrow \, \exists y \, S(y,x))$
I.e., every element except the first element has an immediate predecessor. -
•
 $\exists x \, B(x)$
I.e.,
$\exists x \, B(x)$
I.e.,
 $B(x)$
holds for some x.
$B(x)$
holds for some x. -
•
 $\forall x \forall y \, (B(x) \,\rightarrow \, x \preceq y)$
I.e., if
$\forall x \forall y \, (B(x) \,\rightarrow \, x \preceq y)$
I.e., if
 $B(x)$
holds, then x is least.
$B(x)$
holds, then x is least. -
•
 $\exists x \, T_0(x)$
I.e.,
$\exists x \, T_0(x)$
I.e.,
 $T_0(x)$
holds for some x.
$T_0(x)$
holds for some x. -
•
 $\exists x \, T_2(x) \;\rightarrow \; \exists x \, T_1(x)$
I.e., if
$\exists x \, T_2(x) \;\rightarrow \; \exists x \, T_1(x)$
I.e., if
 $T_2(x)$
holds for some x, then
$T_2(x)$
holds for some x, then
 $T_1(x)$
holds for some x.
$T_1(x)$
holds for some x. -
• For each
 $i \leq 2$
,
$i \leq 2$
,
 $\neg \exists ^{\geq 2} x \, T_i(x)$
I.e., for each
$\neg \exists ^{\geq 2} x \, T_i(x)$
I.e., for each
 $i \leq 2$
, there is at most one x for which
$i \leq 2$
, there is at most one x for which
 $T_i(x)$
holds.
$T_i(x)$
holds. -
•
 $\forall x \forall y \, (T_2(x) \,\rightarrow \, y \preceq x)$
I.e., if
$\forall x \forall y \, (T_2(x) \,\rightarrow \, y \preceq x)$
I.e., if
 $T_2(x)$
holds for x, then x is greatest.
$T_2(x)$
holds for x, then x is greatest. -
•
 $\neg \exists x\, T_2(x) \;\rightarrow \; \forall x \forall y \, (T_1(x) \,\rightarrow \, y \preceq x)$
I.e., if
$\neg \exists x\, T_2(x) \;\rightarrow \; \forall x \forall y \, (T_1(x) \,\rightarrow \, y \preceq x)$
I.e., if
 $T_2(x)$
does not hold for any element but
$T_2(x)$
does not hold for any element but
 $T_1(x)$
holds for x, then x is greatest.
$T_1(x)$
holds for x, then x is greatest. -
•
 $\neg \exists x\, T_1(x) \;\rightarrow \; \forall x \forall y \, (T_0(x) \,\rightarrow \, y \preceq x)$
I.e., if
$\neg \exists x\, T_1(x) \;\rightarrow \; \forall x \forall y \, (T_0(x) \,\rightarrow \, y \preceq x)$
I.e., if
 $T_1(x)$
does not hold for any element but
$T_1(x)$
does not hold for any element but
 $T_0(x)$
holds for x, then x is greatest.
$T_0(x)$
holds for x, then x is greatest.
Notice that from
![]() $\Gamma $
it can be deduced that there is a unique element satisfying
$\Gamma $
it can be deduced that there is a unique element satisfying
![]() $B(x)$
and a unique element satisfying
$B(x)$
and a unique element satisfying
![]() $T_0(x)$
. So we could have used constant symbols in place of B and
$T_0(x)$
. So we could have used constant symbols in place of B and
![]() $T_0$
. We prefer the symmetry of a relational language. Also notice that from
$T_0$
. We prefer the symmetry of a relational language. Also notice that from
![]() $\Gamma $
it can be deduced that there is a
$\Gamma $
it can be deduced that there is a
![]() $\prec $
-least element and a
$\prec $
-least element and a
![]() $\prec $
-greatest element. Finally, notice that every sentence in
$\prec $
-greatest element. Finally, notice that every sentence in
![]() $\Gamma $
is equivalent to a
$\Gamma $
is equivalent to a
![]() $\Pi _2$
sentence.
$\Pi _2$
sentence.
When shuffling infinite collections of finite linear orders into a cohesive power of a computable copy of
![]() $\omega $
, we start with a computable colored copy of
$\omega $
, we start with a computable colored copy of
![]() $\omega $
and replace its elements by arbitrarily large finite linear orders. If the finite linear orders can be uniformly computably expanded to models of
$\omega $
and replace its elements by arbitrarily large finite linear orders. If the finite linear orders can be uniformly computably expanded to models of
![]() $\Gamma $
, then this replacement process naturally shuffles the linear order
$\Gamma $
, then this replacement process naturally shuffles the linear order
![]() $\omega + \zeta \eta + \omega ^*$
into the cohesive power. Lemma 6.7, which implies that
$\omega + \zeta \eta + \omega ^*$
into the cohesive power. Lemma 6.7, which implies that
![]() $\omega + \boldsymbol {\sigma }(\{\omega + \zeta \eta + \omega ^*\})$
can be achieved as the order-type of a cohesive power of a computable copy of
$\omega + \boldsymbol {\sigma }(\{\omega + \zeta \eta + \omega ^*\})$
can be achieved as the order-type of a cohesive power of a computable copy of
![]() $\omega $
, serves as an example explaining this phenomenon.
$\omega $
, serves as an example explaining this phenomenon.
Lemma 6.6. Let
![]() $(\mathcal {M}_n : n \in I)$
be a uniformly computable sequence of
$(\mathcal {M}_n : n \in I)$
be a uniformly computable sequence of
![]() $\mathfrak {O}$
-structures that are all finite models of
$\mathfrak {O}$
-structures that are all finite models of
![]() $\Gamma $
, indexed by a computable
$\Gamma $
, indexed by a computable
![]() $I \subseteq \mathbb {N}$
. Let
$I \subseteq \mathbb {N}$
. Let
![]() $M_n$
denote the domain of
$M_n$
denote the domain of
![]() $\mathcal {M}_n$
for each
$\mathcal {M}_n$
for each
![]() $n \in I$
. Let C be a cohesive set. Let
$n \in I$
. Let C be a cohesive set. Let
![]() $\theta \colon \mathbb {N} \rightarrow I$
be a partial computable function with
$\theta \colon \mathbb {N} \rightarrow I$
be a partial computable function with
![]() $C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
. Suppose that
$C \subseteq ^* \operatorname {{\mathrm {dom}}}(\theta )$
. Suppose that
![]() $\lim _{n \in C} |M_{\theta (n)}| = \infty $
. Then, as a linear order,
$\lim _{n \in C} |M_{\theta (n)}| = \infty $
. Then, as a linear order,
![]() $\prod _C \mathcal {M}_{\theta (n)}$
has order-type
$\prod _C \mathcal {M}_{\theta (n)}$
has order-type
![]() $\omega + \zeta \eta + \omega ^*$
.
$\omega + \zeta \eta + \omega ^*$
.
Proof We have that
![]() $\mathcal {M}_n \models \Gamma $
for each
$\mathcal {M}_n \models \Gamma $
for each
![]() $n \in I$
by assumption and that each sentence of
$n \in I$
by assumption and that each sentence of
![]() $\Gamma $
is equivalent to a
$\Gamma $
is equivalent to a
![]() $\Pi _2$
sentence. Therefore
$\Pi _2$
sentence. Therefore
![]() $\prod _C \mathcal {M}_{\theta (n)} \models \Gamma $
by Theorem 2.7 item (2). Thus
$\prod _C \mathcal {M}_{\theta (n)} \models \Gamma $
by Theorem 2.7 item (2). Thus
![]() $\prod _C \mathcal {M}_{\theta (n)}$
has a
$\prod _C \mathcal {M}_{\theta (n)}$
has a
![]() $\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-least element and a
$\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-least element and a
![]() $\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-greatest element (as these facts can be deduced from
$\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-greatest element (as these facts can be deduced from
![]() $\Gamma $
), every element that is not
$\Gamma $
), every element that is not
![]() $\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-least has a
$\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-least has a
![]() $\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-immediate successor, and every element that is not
$\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-immediate successor, and every element that is not
![]() $\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-greatest has a
$\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-greatest has a
![]() $\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-immediate predecessor. Furthermore,
$\prec _{\prod _C \mathcal {M}_{\theta (n)}}$
-immediate predecessor. Furthermore,
![]() $\prod _C \mathcal {M}_{\theta (n)}$
is infinite because
$\prod _C \mathcal {M}_{\theta (n)}$
is infinite because
![]() $\lim _{n \in C} |M_{\theta (n)}| = \infty $
. Thus as a linear order,
$\lim _{n \in C} |M_{\theta (n)}| = \infty $
. Thus as a linear order,
![]() $\prod _C \mathcal {M}_{\theta (n)}$
must consist of an initial block of order-type
$\prod _C \mathcal {M}_{\theta (n)}$
must consist of an initial block of order-type
![]() $\omega $
, a final block of order-type
$\omega $
, a final block of order-type
![]() $\omega ^*$
, and intermediate blocks of order-type
$\omega ^*$
, and intermediate blocks of order-type
![]() $\zeta $
. We show that the blocks of
$\zeta $
. We show that the blocks of
![]() $\prod _C \mathcal {M}_{\theta (n)}$
are dense.
$\prod _C \mathcal {M}_{\theta (n)}$
are dense.
If C were co-c.e. or the sequence
![]() $(\mathcal {M}_n : n \in I)$
were uniformly
$(\mathcal {M}_n : n \in I)$
were uniformly
![]() $1$
-decidable, then we could use a saturation argument to conclude that the blocks of
$1$
-decidable, then we could use a saturation argument to conclude that the blocks of
![]() $\prod _C \mathcal {M}_{\theta (n)}$
are dense. However, C is not necessarily co-c.e., and, although each individual structure
$\prod _C \mathcal {M}_{\theta (n)}$
are dense. However, C is not necessarily co-c.e., and, although each individual structure
![]() $\mathcal {M}_n$
is finite and hence decidable, the sequence
$\mathcal {M}_n$
is finite and hence decidable, the sequence
![]() $(\mathcal {M}_n : n \in I)$
need not be uniformly
$(\mathcal {M}_n : n \in I)$
need not be uniformly
![]() $1$
-decidable. We therefore resort to an ad hoc argument.
$1$
-decidable. We therefore resort to an ad hoc argument.
Let
![]() $[\varphi ], [\psi ] \in |\prod _C \mathcal {M}_{\theta (n)}|$
be such that
$[\varphi ], [\psi ] \in |\prod _C \mathcal {M}_{\theta (n)}|$
be such that
![]() . Then
. Then
![]() $\lim _{n \in C}|(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}| = \infty $
by Lemma 3.8. If
$\lim _{n \in C}|(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}| = \infty $
by Lemma 3.8. If
![]() $\theta (n){\downarrow }$
,
$\theta (n){\downarrow }$
,
![]() $\varphi (n){\downarrow }$
,
$\varphi (n){\downarrow }$
,
![]() $\psi (n){\downarrow }$
, and
$\psi (n){\downarrow }$
, and
![]() $\psi (n) \prec _{\mathcal {M}_{\theta (n)}} \varphi (n)$
, then we can effectively determine the size of the interval
$\psi (n) \prec _{\mathcal {M}_{\theta (n)}} \varphi (n)$
, then we can effectively determine the size of the interval
![]() $(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}$
as follows. Search for
$(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}$
as follows. Search for
![]() $x_0, \dots , x_{k-1} \in M_{\theta (n)}$
such that
$x_0, \dots , x_{k-1} \in M_{\theta (n)}$
such that
![]() $S^{\mathcal {M}_{\theta (n)}}(\psi (n), x_0)$
holds, such that
$S^{\mathcal {M}_{\theta (n)}}(\psi (n), x_0)$
holds, such that
![]() $S^{\mathcal {M}_{\theta (n)}}(x_i, x_{i+1})$
holds for each
$S^{\mathcal {M}_{\theta (n)}}(x_i, x_{i+1})$
holds for each
![]() $i < k-1$
, and such that
$i < k-1$
, and such that
![]() $S^{\mathcal {M}_{\theta (n)}}(x_{k-1}, \varphi (n))$
holds. Then
$S^{\mathcal {M}_{\theta (n)}}(x_{k-1}, \varphi (n))$
holds. Then
![]() $|(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}| = k$
. Such a sequence
$|(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}| = k$
. Such a sequence
![]() $x_0, \dots , x_{k-1}$
exists because
$x_0, \dots , x_{k-1}$
exists because
![]() $\mathcal {M}_{\theta (n)}$
is finite and
$\mathcal {M}_{\theta (n)}$
is finite and
![]() $S^{\mathcal {M}_{\theta (n)}}$
is the
$S^{\mathcal {M}_{\theta (n)}}$
is the
![]() $\prec _{\mathcal {M}_{\theta (n)}}$
-immediate successor relation on
$\prec _{\mathcal {M}_{\theta (n)}}$
-immediate successor relation on
![]() $\mathcal {M}_{\theta (n)}$
.
$\mathcal {M}_{\theta (n)}$
.
Define a partial computable function
![]() $\rho $
as follows. Given n, if
$\rho $
as follows. Given n, if
![]() $\theta (n){\downarrow }$
,
$\theta (n){\downarrow }$
,
![]() $\varphi (n){\downarrow }$
,
$\varphi (n){\downarrow }$
,
![]() $\psi (n){\downarrow }$
, and
$\psi (n){\downarrow }$
, and
![]() $\psi (n) \prec _{\mathcal {M}_{\theta (n)}} \varphi (n)$
, then determine the size k of the interval
$\psi (n) \prec _{\mathcal {M}_{\theta (n)}} \varphi (n)$
, then determine the size k of the interval
![]() $(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}$
according to the procedure described above. If
$(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}$
according to the procedure described above. If
![]() $k> 0$
, then locate the
$k> 0$
, then locate the
![]() th
th
![]() $\prec _{\mathcal {M}_{\theta (n)}}$
-least element x of
$\prec _{\mathcal {M}_{\theta (n)}}$
-least element x of
![]() $(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}$
, and output
$(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}$
, and output
![]() $\rho (n) = x$
. Otherwise
$\rho (n) = x$
. Otherwise
![]() $\rho (n){\uparrow }$
. As
$\rho (n){\uparrow }$
. As
![]() $\lim _{n \in C}|(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}| = \infty $
, it follows that both
$\lim _{n \in C}|(\psi (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}| = \infty $
, it follows that both
![]() $\lim _{n \in C}|(\psi (n), \rho (n))_{\mathcal {M}_{\theta (n)}}| = \infty $
and
$\lim _{n \in C}|(\psi (n), \rho (n))_{\mathcal {M}_{\theta (n)}}| = \infty $
and
![]() $\lim _{n \in C}|(\rho (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}| = \infty $
. Thus
$\lim _{n \in C}|(\rho (n), \varphi (n))_{\mathcal {M}_{\theta (n)}}| = \infty $
. Thus
![]() again by Lemma 3.8. Therefore the blocks of
again by Lemma 3.8. Therefore the blocks of
![]() $\prod _C \mathcal {M}_{\theta (n)}$
are dense.
$\prod _C \mathcal {M}_{\theta (n)}$
are dense.
As a linear order,
![]() $\prod _C \mathcal {M}_{\theta (n)}$
is countably infinite, has a least block of order-type
$\prod _C \mathcal {M}_{\theta (n)}$
is countably infinite, has a least block of order-type
![]() $\omega $
, has a greatest block of order-type
$\omega $
, has a greatest block of order-type
![]() $\omega ^*$
, has intermediate blocks of order-type
$\omega ^*$
, has intermediate blocks of order-type
![]() $\zeta $
, and the blocks are dense. Thus
$\zeta $
, and the blocks are dense. Thus
![]() $\prod _C \mathcal {M}_{\theta (n)}$
has order-type
$\prod _C \mathcal {M}_{\theta (n)}$
has order-type
![]() $\omega + \zeta \eta + \omega ^*$
as a linear order.
$\omega + \zeta \eta + \omega ^*$
as a linear order.
In Lemma 6.6, it is necessary that the structures
![]() $(\mathcal {M}_n : n \in I)$
satisfy additional assumptions (such as being models of
$(\mathcal {M}_n : n \in I)$
satisfy additional assumptions (such as being models of
![]() $\Gamma $
) beyond merely being finite linear orders. For example, recall from Proposition 4.10 that a cohesive product of finite linear orders need not have a maximum element.
$\Gamma $
) beyond merely being finite linear orders. For example, recall from Proposition 4.10 that a cohesive product of finite linear orders need not have a maximum element.
Lemma 6.7. Let
![]() $\mathcal {O}$
be a computable colored copy of
$\mathcal {O}$
be a computable colored copy of
![]() $\omega $
. There is a computable copy
$\omega $
. There is a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
(constructed from
$\omega $
(constructed from
![]() $\mathcal {O}$
) such that for every cohesive set C, if
$\mathcal {O}$
) such that for every cohesive set C, if
![]() $\prod _C \mathcal {O}$
is colorful, then
$\prod _C \mathcal {O}$
is colorful, then
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + (\omega + \zeta \eta + \omega ^*)\eta $
, which is the same as
$\omega + (\omega + \zeta \eta + \omega ^*)\eta $
, which is the same as
![]() $\omega + \boldsymbol {\sigma }(\{\omega + \zeta \eta + \omega ^*\})$
.
$\omega + \boldsymbol {\sigma }(\{\omega + \zeta \eta + \omega ^*\})$
.
Proof Let
![]() $\mathcal {O} = (R, \mathbb {N}, \prec _{\mathcal {R}}, F)$
be a computable colored copy of
$\mathcal {O} = (R, \mathbb {N}, \prec _{\mathcal {R}}, F)$
be a computable colored copy of
![]() $\omega $
, and let
$\omega $
, and let
![]() $\mathcal {R}$
denote
$\mathcal {R}$
denote
![]() $(R, \prec _{\mathcal {R}})$
. Let
$(R, \prec _{\mathcal {R}})$
. Let
![]() $(\mathcal {M}_r : r \in R)$
be the uniformly computable sequence of linear orders where
$(\mathcal {M}_r : r \in R)$
be the uniformly computable sequence of linear orders where
![]() $\mathcal {M}_r = \boldsymbol {r+1}$
for each
$\mathcal {M}_r = \boldsymbol {r+1}$
for each
![]() $r \in R$
. Let
$r \in R$
. Let
![]() $\mathcal {L}$
be the generalized sum
$\mathcal {L}$
be the generalized sum
![]() $\mathcal {L} = \sum _{r \in R} \mathcal {M}_r$
. Then
$\mathcal {L} = \sum _{r \in R} \mathcal {M}_r$
. Then
![]() $\mathcal {L}$
is a computable copy of
$\mathcal {L}$
is a computable copy of
![]() $\omega $
.
$\omega $
.
Let C be a cohesive set for which
![]() $\prod _C \mathcal {O}$
is colorful. We need to show that
$\prod _C \mathcal {O}$
is colorful. We need to show that
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + (\omega + \zeta \eta + \omega ^*)\eta $
.
$\omega + (\omega + \zeta \eta + \omega ^*)\eta $
.
By Theorem 6.3,
 $$ \begin{align*} \prod\nolimits_C \mathcal{L} \quad=\quad \prod\nolimits_C \sum_{r \in R}\mathcal{M}_r \quad\cong\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|}\prod\nolimits_C \mathcal{M}_{\theta(n)}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathcal{L} \quad=\quad \prod\nolimits_C \sum_{r \in R}\mathcal{M}_r \quad\cong\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|}\prod\nolimits_C \mathcal{M}_{\theta(n)}. \end{align*} $$
As in the proof of Lemma 6.5, let
![]() $\mathcal {Z}$
denote
$\mathcal {Z}$
denote
![]() $\sum _{[\theta ] \in \left |\prod _C \mathcal {R}\right |}\prod _C \mathcal {M}_{\theta (n)}$
; let
$\sum _{[\theta ] \in \left |\prod _C \mathcal {R}\right |}\prod _C \mathcal {M}_{\theta (n)}$
; let
![]() $|\prod _C \mathcal {R}|_{\mathrm {std}}$
and
$|\prod _C \mathcal {R}|_{\mathrm {std}}$
and
![]() $|\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
denote the standard and non-standard parts of
$|\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
denote the standard and non-standard parts of
![]() $\prod _C \mathcal {R}$
; and let
$\prod _C \mathcal {R}$
; and let
 $$ \begin{align*} \mathcal{Z}_{\mathrm{std}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{std}}}\prod\nolimits_C \mathcal{M}_{\theta(n)},\\ \mathcal{Z}_{\mathrm{nonstd}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{nonstd}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \end{align*} $$
$$ \begin{align*} \mathcal{Z}_{\mathrm{std}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{std}}}\prod\nolimits_C \mathcal{M}_{\theta(n)},\\ \mathcal{Z}_{\mathrm{nonstd}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{nonstd}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \end{align*} $$
so that
![]() $\mathcal {Z} \cong \mathcal {Z}_{\mathrm {std}} + \mathcal {Z}_{\mathrm {nonstd}}$
. The fact that
$\mathcal {Z} \cong \mathcal {Z}_{\mathrm {std}} + \mathcal {Z}_{\mathrm {nonstd}}$
. The fact that
![]() $\prod _C \mathcal {O}$
is colorful implies that
$\prod _C \mathcal {O}$
is colorful implies that
![]() $|\prod _C \mathcal {R}|_{\mathrm {nonstd}} \cong \eta $
.
$|\prod _C \mathcal {R}|_{\mathrm {nonstd}} \cong \eta $
.
If
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {std}}$
, then there is an
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {std}}$
, then there is an
![]() $r \in R$
such that
$r \in R$
such that
![]() $(\forall ^\infty n \in C)(\theta (n) = r)$
. Therefore
$(\forall ^\infty n \in C)(\theta (n) = r)$
. Therefore
![]() $(\forall ^\infty n \in C)(\mathcal {M}_{\theta (n)} = \boldsymbol {r+1})$
, so
$(\forall ^\infty n \in C)(\mathcal {M}_{\theta (n)} = \boldsymbol {r+1})$
, so
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {r+1}$
by Lemma 6.4. This means that
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {r+1}$
by Lemma 6.4. This means that
![]() $\mathcal {Z}_{\mathrm {std}}$
is a generalized sum of finite linear orders over a copy of
$\mathcal {Z}_{\mathrm {std}}$
is a generalized sum of finite linear orders over a copy of
![]() $\omega $
, so
$\omega $
, so
![]() $\mathcal {Z}_{\mathrm {std}} \cong \omega $
.
$\mathcal {Z}_{\mathrm {std}} \cong \omega $
.
If
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
, then
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
, then
![]() $\lim _{n \in C} \theta (n) = \infty $
by Lemma 4.2. Letting
$\lim _{n \in C} \theta (n) = \infty $
by Lemma 4.2. Letting
![]() $M_r$
denote the domain
$M_r$
denote the domain
![]() $\{0, 1, \dots , r\}$
of
$\{0, 1, \dots , r\}$
of
![]() $\mathcal {M}_r$
for each
$\mathcal {M}_r$
for each
![]() $r \in R$
, we have that
$r \in R$
, we have that
![]() $\lim _{n \in C}|M_{\theta (n)}| = \infty $
. Then
$\lim _{n \in C}|M_{\theta (n)}| = \infty $
. Then
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
by Lemma 6.6. To see that Lemma 6.6 applies in this simplified situation, note that we can uniformly computably expand the linear orders
$\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
by Lemma 6.6. To see that Lemma 6.6 applies in this simplified situation, note that we can uniformly computably expand the linear orders
![]() $(\mathcal {M}_r : r \in R)$
to
$(\mathcal {M}_r : r \in R)$
to
![]() $\mathfrak {O}$
-structures that are models of
$\mathfrak {O}$
-structures that are models of
![]() $\Gamma $
. For
$\Gamma $
. For
![]() $\mathcal {M}_r = \boldsymbol {r+1}$
, define S to be the usual immediate successor relation, define
$\mathcal {M}_r = \boldsymbol {r+1}$
, define S to be the usual immediate successor relation, define
![]() $B(x)$
to hold exactly when
$B(x)$
to hold exactly when
![]() $x = 0$
, define
$x = 0$
, define
![]() $T_0(x)$
to hold exactly when
$T_0(x)$
to hold exactly when
![]() $x = r$
, and define
$x = r$
, and define
![]() $T_1(x)$
and
$T_1(x)$
and
![]() $T_2(x)$
to hold of no element.
$T_2(x)$
to hold of no element.
We just showed that
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
for each
$\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
for each
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
. Therefore
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
. Therefore
![]() $\mathcal {Z}_{\mathrm {nonstd}} \;\cong \; \omega + (\omega + \zeta \eta + \omega ^*)\eta \;\cong \; \omega + \boldsymbol {\sigma }(\{\omega + \zeta \eta + \omega ^*\})$
. Thus
$\mathcal {Z}_{\mathrm {nonstd}} \;\cong \; \omega + (\omega + \zeta \eta + \omega ^*)\eta \;\cong \; \omega + \boldsymbol {\sigma }(\{\omega + \zeta \eta + \omega ^*\})$
. Thus
 $$ \begin{align*} \prod\nolimits_C \mathcal{L} \quad&\cong\quad \mathcal{Z} \quad\cong\quad \mathcal{Z}_{\mathrm{std}} + \mathcal{Z}_{\mathrm{nonstd}} \quad\cong\quad \omega + (\omega + \zeta\eta + \omega^*)\eta\\ &\cong\quad \omega + \boldsymbol{\sigma}(\{\omega + \zeta\eta + \omega^*\}), \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathcal{L} \quad&\cong\quad \mathcal{Z} \quad\cong\quad \mathcal{Z}_{\mathrm{std}} + \mathcal{Z}_{\mathrm{nonstd}} \quad\cong\quad \omega + (\omega + \zeta\eta + \omega^*)\eta\\ &\cong\quad \omega + \boldsymbol{\sigma}(\{\omega + \zeta\eta + \omega^*\}), \end{align*} $$
as desired.
We are finally ready to handle shuffles of the form
![]() $\boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
, where
$\boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
, where
![]() $X \subseteq \mathbb {N} \setminus \{0\}$
is a Boolean combination of
$X \subseteq \mathbb {N} \setminus \{0\}$
is a Boolean combination of
![]() $\Sigma _2$
sets thought of as a set of finite order-types. We proceed in two steps. Lemma 6.8 handles the case where X is the intersection of a
$\Sigma _2$
sets thought of as a set of finite order-types. We proceed in two steps. Lemma 6.8 handles the case where X is the intersection of a
![]() $\Sigma _2$
set and a
$\Sigma _2$
set and a
![]() $\Pi _2$
set, and Lemma 6.9 extends the method to finite unions of such sets.
$\Pi _2$
set, and Lemma 6.9 extends the method to finite unions of such sets.
Lemma 6.8. Let
![]() $X \subseteq \mathbb {N} \setminus \{0\}$
be the intersection of a
$X \subseteq \mathbb {N} \setminus \{0\}$
be the intersection of a
![]() $\Sigma _2$
set and a
$\Sigma _2$
set and a
![]() $\Pi _2$
set, thought of as a set of finite order-types. Let
$\Pi _2$
set, thought of as a set of finite order-types. Let
![]() $\mathcal {O}$
be a computable colored copy of
$\mathcal {O}$
be a computable colored copy of
![]() $\omega $
. There is a computable copy
$\omega $
. There is a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
(constructed from
$\omega $
(constructed from
![]() $\mathcal {O}$
) such that for every cohesive set C, if
$\mathcal {O}$
) such that for every cohesive set C, if
![]() $\prod _C \mathcal {O}$
is colorful, then
$\prod _C \mathcal {O}$
is colorful, then
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
.
$\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
.
Proof The
![]() $X = \emptyset $
case is Lemma 6.7, so we may assume that
$X = \emptyset $
case is Lemma 6.7, so we may assume that
![]() $X \neq \emptyset $
. Let
$X \neq \emptyset $
. Let
![]() $k_0$
be the least element of X. Let P and Q be computable predicates for which
$k_0$
be the least element of X. Let P and Q be computable predicates for which
Let
![]() $\mathcal {O} = (R, \mathbb {N}, \prec _{\mathcal {R}}, F)$
be a computable colored copy of
$\mathcal {O} = (R, \mathbb {N}, \prec _{\mathcal {R}}, F)$
be a computable colored copy of
![]() $\omega $
, and let
$\omega $
, and let
![]() $\mathcal {R}$
denote
$\mathcal {R}$
denote
![]() $(R, \prec _{\mathcal {R}})$
. We define a uniformly computable sequence
$(R, \prec _{\mathcal {R}})$
. We define a uniformly computable sequence
![]() $(\mathcal {M}_r : r \in R)$
of
$(\mathcal {M}_r : r \in R)$
of
![]() $\mathfrak {O}$
-structures that are finite models of
$\mathfrak {O}$
-structures that are finite models of
![]() $\Gamma $
and have the following properties. Let
$\Gamma $
and have the following properties. Let
![]() $M_r$
denote the domain of
$M_r$
denote the domain of
![]() $\mathcal {M}_r$
for each
$\mathcal {M}_r$
for each
![]() $r \in R$
.
$r \in R$
.
-
(1) If
 $k \in X$
, then
$k \in X$
, then
 $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k)$
.
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k)$
. -
(2) If
 $k < k_0$
, then
$k < k_0$
, then
 $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
.
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
. -
(3) If
 $k> k_0$
and
$k> k_0$
and
 $k \notin X$
, then either
$k \notin X$
, then either
 $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k_0)$
or
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k_0)$
or
 $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
.
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
.
We then take
![]() $\mathcal {L}$
to be the generalized sum
$\mathcal {L}$
to be the generalized sum
![]() $\sum _{r \in R} (\mathcal {M}_r {\restriction } {\prec })$
of the sequence
$\sum _{r \in R} (\mathcal {M}_r {\restriction } {\prec })$
of the sequence
![]() $(\mathcal {M}_r : r \in R)$
, viewed as a sequence of finite linear orders, over the linear order
$(\mathcal {M}_r : r \in R)$
, viewed as a sequence of finite linear orders, over the linear order
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
To compute
![]() $\mathcal {M}_r = (M_r, \prec , S, B, T_0, T_1, T_2)$
, first initialize
$\mathcal {M}_r = (M_r, \prec , S, B, T_0, T_1, T_2)$
, first initialize
![]() $\mathcal {M}_r$
on
$\mathcal {M}_r$
on
![]() $\{0, \dots , k_0 - 1\}$
as follows:
$\{0, \dots , k_0 - 1\}$
as follows:
-
•
 $\{0, \dots , k_0 - 1\} \subseteq M_r$
.
$\{0, \dots , k_0 - 1\} \subseteq M_r$
. -
•
 $\prec $
agrees with the usual order
$\prec $
agrees with the usual order
 $<$
on
$<$
on
 $\{0, \dots , k_0 - 1\}$
.
$\{0, \dots , k_0 - 1\}$
. -
• S is the usual successor relation on
 $\{0, \dots , k_0 - 1\}$
.
$\{0, \dots , k_0 - 1\}$
. -
•
 $B(x)$
holds if and only if
$B(x)$
holds if and only if
 $x = 0$
.
$x = 0$
. -
•
 $T_0(x)$
holds if and only if
$T_0(x)$
holds if and only if
 $x = k_0 - 1$
.
$x = k_0 - 1$
. -
• Neither
 $T_1(x)$
nor
$T_1(x)$
nor
 $T_2(x)$
hold of any
$T_2(x)$
hold of any
 $x \in \{0, \dots , k_0 - 1\}$
.
$x \in \{0, \dots , k_0 - 1\}$
.
If
![]() $F(r) = k_0$
, or if
$F(r) = k_0$
, or if
![]() $F(r) < k_0$
and
$F(r) < k_0$
and
![]() $r < k_0$
, then define
$r < k_0$
, then define
![]() $x \notin M_r$
for all
$x \notin M_r$
for all
![]() $x \geq k_0$
. In this case,
$x \geq k_0$
. In this case,
![]() $\mathcal {M}_r$
is the usual presentation of the linear order
$\mathcal {M}_r$
is the usual presentation of the linear order
![]() $\boldsymbol {k}_0$
expanded by S, B,
$\boldsymbol {k}_0$
expanded by S, B,
![]() $T_0$
,
$T_0$
,
![]() $T_1$
, and
$T_1$
, and
![]() $T_2$
as described above. It is straightforward to check that
$T_2$
as described above. It is straightforward to check that
![]() $\mathcal {M}_r \models \Gamma $
.
$\mathcal {M}_r \models \Gamma $
.
If
![]() $F(r) < k_0$
and
$F(r) < k_0$
and
![]() $r \geq k_0$
, then add
$r \geq k_0$
, then add
![]() $k_0, \dots , r$
to
$k_0, \dots , r$
to
![]() $M_r$
so that
$M_r$
so that
![]() $M_r = \{0, \dots , r\}$
. Extend
$M_r = \{0, \dots , r\}$
. Extend
![]() $\prec $
to agree with the usual order on
$\prec $
to agree with the usual order on
![]() $\{0, \dots , r\}$
, and extend S to be the corresponding successor relation. Define
$\{0, \dots , r\}$
, and extend S to be the corresponding successor relation. Define
![]() $T_1(x)$
to hold if and only if
$T_1(x)$
to hold if and only if
![]() $x = r$
, and define
$x = r$
, and define
![]() $T_2(x)$
to hold of no
$T_2(x)$
to hold of no
![]() $x \in M_r$
. Define
$x \in M_r$
. Define
![]() $x \notin M_r$
for all
$x \notin M_r$
for all
![]() $x> r$
. In this case,
$x> r$
. In this case,
![]() $\mathcal {M}_r$
is the usual presentation of the linear order
$\mathcal {M}_r$
is the usual presentation of the linear order
![]() $\boldsymbol {r+1}$
expanded by S, B,
$\boldsymbol {r+1}$
expanded by S, B,
![]() $T_0$
,
$T_0$
,
![]() $T_1$
, and
$T_1$
, and
![]() $T_2$
, where
$T_2$
, where
![]() $T_0(x)$
holds only of
$T_0(x)$
holds only of
![]() $k_0 - 1$
,
$k_0 - 1$
,
![]() $T_1(x)$
holds only of r, and
$T_1(x)$
holds only of r, and
![]() $T_2(x)$
holds of no element. It is again straightforward to check that
$T_2(x)$
holds of no element. It is again straightforward to check that
![]() $\mathcal {M}_r \models \Gamma $
.
$\mathcal {M}_r \models \Gamma $
.
If
![]() $F(r)> k_0$
, then compute
$F(r)> k_0$
, then compute
![]() $\mathcal {M}_r$
in stages. At all stages s, we maintain that
$\mathcal {M}_r$
in stages. At all stages s, we maintain that
![]() $\mathcal {M}_r \models \Gamma $
and that
$\mathcal {M}_r \models \Gamma $
and that
![]() $\prec $
agrees with the usual order
$\prec $
agrees with the usual order
![]() $<$
on the elements of
$<$
on the elements of
![]() $\mathcal {M}_r$
. For every x, we decide whether or not
$\mathcal {M}_r$
. For every x, we decide whether or not
![]() $x \in M_r$
at stage x at the latest. The initialization of
$x \in M_r$
at stage x at the latest. The initialization of
![]() $\mathcal {M}_r$
on
$\mathcal {M}_r$
on
![]() $\{0, \dots , k_0 - 1\}$
described above counts as stage
$\{0, \dots , k_0 - 1\}$
described above counts as stage
![]() $0$
, so
$0$
, so
![]() $\mathcal {M}_r \models \Gamma $
at the end of stage
$\mathcal {M}_r \models \Gamma $
at the end of stage
![]() $0$
. Proceed as follows at stage
$0$
. Proceed as follows at stage
![]() $s> 0$
. If it has not yet been decided whether
$s> 0$
. If it has not yet been decided whether
![]() $s \in M_r$
by the beginning of stage s, then define
$s \in M_r$
by the beginning of stage s, then define
![]() $s \notin M_r$
. Then act according to the following cases.
$s \notin M_r$
. Then act according to the following cases.
-
Case 1:
 $M_r$
is still
$M_r$
is still
 $\{0, \dots , k_0 - 1\}$
at the beginning of stage s,
$\{0, \dots , k_0 - 1\}$
at the beginning of stage s,
 $(\exists a < r)(\forall b < s)\, P(F(r), a, b)$
holds, and
$(\exists a < r)(\forall b < s)\, P(F(r), a, b)$
holds, and
 $(\forall a < r)(\exists b < s)\, Q(F(r), a, b)$
holds. In this case, let
$(\forall a < r)(\exists b < s)\, Q(F(r), a, b)$
holds. In this case, let
 $s < x_0 < x_1 < \dots < x_{F(r) - k_0 - 1}$
be the
$s < x_0 < x_1 < \dots < x_{F(r) - k_0 - 1}$
be the
 $F(r) - k_0$
least numbers
$F(r) - k_0$
least numbers
 $x> s$
for which it has not yet been decided whether
$x> s$
for which it has not yet been decided whether
 $x \in M_r$
. Add
$x \in M_r$
. Add
 $x_0, \dots , x_{F(r) - k_0 - 1}$
to
$x_0, \dots , x_{F(r) - k_0 - 1}$
to
 $M_r$
so that
$M_r$
so that
 $M_r = \{0, \dots , k_0 - 1, x_0, \dots , x_{F(r) - k_0 - 1}\}$
. Extend
$M_r = \{0, \dots , k_0 - 1, x_0, \dots , x_{F(r) - k_0 - 1}\}$
. Extend
 $\prec $
to agree with the usual order on
$\prec $
to agree with the usual order on
 $\{0, \dots , k_0 - 1, x_0, \dots , x_{F(r) - k_0 - 1}\}$
, and extend S to be the corresponding successor relation. So
$\{0, \dots , k_0 - 1, x_0, \dots , x_{F(r) - k_0 - 1}\}$
, and extend S to be the corresponding successor relation. So
 $S(k_0 - 1, x_0)$
holds, and
$S(k_0 - 1, x_0)$
holds, and
 $S(x_i, x_{i+1})$
holds for all
$S(x_i, x_{i+1})$
holds for all
 $i < F(r) - k_0 - 1$
. Finally, define
$i < F(r) - k_0 - 1$
. Finally, define
 $T_1(x)$
to hold if and only if
$T_1(x)$
to hold if and only if
 $x = x_{F(r) - k_0 - 1}$
, and define
$x = x_{F(r) - k_0 - 1}$
, and define
 $T_2(x)$
to hold of no
$T_2(x)$
to hold of no
 $x \in M_r$
. Go on to stage
$x \in M_r$
. Go on to stage
 $s+1$
. Observe that
$s+1$
. Observe that
 $|M_r| = F(r)$
at the end of stage s.
$|M_r| = F(r)$
at the end of stage s.To see that
 $\mathcal {M}_r \models \Gamma $
at the end of stage s, observe that no elements were added to
$\mathcal {M}_r \models \Gamma $
at the end of stage s, observe that no elements were added to
 $\mathcal {M}_r$
between its initialization and the start of stage s. Thus at the start of stage s,
$\mathcal {M}_r$
between its initialization and the start of stage s. Thus at the start of stage s,
 $T_0(x)$
holds of one element, and
$T_0(x)$
holds of one element, and
 $T_1(x)$
and
$T_1(x)$
and
 $T_2(x)$
hold of no element. During stage s, a new greatest element
$T_2(x)$
hold of no element. During stage s, a new greatest element
 $x_{F(r) - k_0 - 1}$
is added, and
$x_{F(r) - k_0 - 1}$
is added, and
 $T_1(x)$
is defined to hold of exactly this element. Also,
$T_1(x)$
is defined to hold of exactly this element. Also,
 $T_2(x)$
still holds of no element at the end of stage s. One may now check that
$T_2(x)$
still holds of no element at the end of stage s. One may now check that
 $\mathcal {M}_r \models \Gamma $
.
$\mathcal {M}_r \models \Gamma $
. -
Case 2:
 $(\forall a < r)(\exists b < s)\, \neg P(F(r), a, b)$
holds and
$(\forall a < r)(\exists b < s)\, \neg P(F(r), a, b)$
holds and
 $|M_r| \leq r$
at the beginning of stage s. In this case, let
$|M_r| \leq r$
at the beginning of stage s. In this case, let
 $m = |M_r|$
, and let
$m = |M_r|$
, and let
 $\ell _0 \prec \ell _1 \prec \cdots \prec \ell _{m-1}$
be the elements of
$\ell _0 \prec \ell _1 \prec \cdots \prec \ell _{m-1}$
be the elements of
 $M_r$
listed in
$M_r$
listed in
 $\prec $
-increasing order. Recall that
$\prec $
-increasing order. Recall that
 $\prec $
and
$\prec $
and
 $<$
agree on
$<$
agree on
 $M_r$
, so also
$M_r$
, so also
 $\ell _0 < \ell _1 < \cdots < \ell _{m-1}$
. Let
$\ell _0 < \ell _1 < \cdots < \ell _{m-1}$
. Let
 $s < x_0 < x_1 < \cdots < x_{r-m}$
be the
$s < x_0 < x_1 < \cdots < x_{r-m}$
be the
 $r+1 - m$
least numbers
$r+1 - m$
least numbers
 $x> s$
for which it has not yet been decided whether
$x> s$
for which it has not yet been decided whether
 $x \in M_r$
. Notice that
$x \in M_r$
. Notice that
 $x_0> \ell _{m-1}$
as well, as otherwise
$x_0> \ell _{m-1}$
as well, as otherwise
 $\ell _{m-1}$
would not have been least when it was added to
$\ell _{m-1}$
would not have been least when it was added to
 $M_r$
. Add
$M_r$
. Add
 $x_0, \dots , x_{r-m}$
to
$x_0, \dots , x_{r-m}$
to
 $M_r$
so that
$M_r$
so that
 $M_r = \{\ell _0, \dots , \ell _{m-1}, x_0, \dots , x_{r-m}\}$
. Extend
$M_r = \{\ell _0, \dots , \ell _{m-1}, x_0, \dots , x_{r-m}\}$
. Extend
 $\prec $
to agree with the usual order on
$\prec $
to agree with the usual order on
 $\{\ell _0, \dots , \ell _{m-1}, x_0, \dots , x_{r-m}\}$
, and extend S to be the corresponding successor relation. So
$\{\ell _0, \dots , \ell _{m-1}, x_0, \dots , x_{r-m}\}$
, and extend S to be the corresponding successor relation. So
 $S(\ell _{m-1}, x_0)$
holds, and
$S(\ell _{m-1}, x_0)$
holds, and
 $S(x_i, x_{i+1})$
holds for all
$S(x_i, x_{i+1})$
holds for all
 $i < r-m$
. If there is no x for which
$i < r-m$
. If there is no x for which
 $T_1(x)$
holds, then define
$T_1(x)$
holds, then define
 $T_1(x)$
to hold if and only if
$T_1(x)$
to hold if and only if
 $x = x_{r-m}$
and define
$x = x_{r-m}$
and define
 $T_2(x)$
to hold of no
$T_2(x)$
to hold of no
 $x \in M_r$
. If there is already an x for which
$x \in M_r$
. If there is already an x for which
 $T_1(x)$
holds, then define
$T_1(x)$
holds, then define
 $T_2(x)$
to hold if and only if
$T_2(x)$
to hold if and only if
 $x = x_{r-m}$
. Go on to stage
$x = x_{r-m}$
. Go on to stage
 $s+1$
. Observe that
$s+1$
. Observe that
 $|M_r| = r+1$
at the end of stage s.
$|M_r| = r+1$
at the end of stage s.Notice that Case 1 and Case 2 can occur at most one time each. After Case 1 occurs,
 $M_r$
is never again
$M_r$
is never again
 $\{0, \dots , k_0 - 1\}$
, so Case 1 never occurs again. After Case 2 occurs, we never again have
$\{0, \dots , k_0 - 1\}$
, so Case 1 never occurs again. After Case 2 occurs, we never again have
 $|M_r| \leq r$
, so Case 2 never occurs again. Thus prior to stage s, Case 2 cannot have occurred (as it is occurring now at stage s), and Case 1 can have occurred at most once. If Case 1 did not occur before stage s, then no elements were added to
$|M_r| \leq r$
, so Case 2 never occurs again. Thus prior to stage s, Case 2 cannot have occurred (as it is occurring now at stage s), and Case 1 can have occurred at most once. If Case 1 did not occur before stage s, then no elements were added to
 $\mathcal {M}_r$
between its initialization and the start of stage s. The situation is then analogous to that of Case 1. We define
$\mathcal {M}_r$
between its initialization and the start of stage s. The situation is then analogous to that of Case 1. We define
 $T_1(x)$
to hold of exactly the new greatest element
$T_1(x)$
to hold of exactly the new greatest element
 $x_{r-m}$
that is added at stage s, and we define
$x_{r-m}$
that is added at stage s, and we define
 $T_2(x)$
to hold of no element. If instead Case 1 did occur before stage s, then at the start of stage s,
$T_2(x)$
to hold of no element. If instead Case 1 did occur before stage s, then at the start of stage s,
 $T_0(x)$
and
$T_0(x)$
and
 $T_1(x)$
hold of exactly one element each, and
$T_1(x)$
hold of exactly one element each, and
 $T_2(x)$
holds of no element. During stage s, a new greatest element
$T_2(x)$
holds of no element. During stage s, a new greatest element
 $x_{r-m}$
is added, and
$x_{r-m}$
is added, and
 $T_2(x)$
is defined to hold of exactly this element. In either situation, one may check that
$T_2(x)$
is defined to hold of exactly this element. In either situation, one may check that
 $\mathcal {M}_r \models \Gamma $
.
$\mathcal {M}_r \models \Gamma $
. -
Case 3: If neither Case 1 nor Case 2 applies, then do nothing more at stage s and go on to stage
 $s+1$
. Then
$s+1$
. Then
 $\mathcal {M}_r \models \Gamma $
at the end of stage s because
$\mathcal {M}_r \models \Gamma $
at the end of stage s because
 $\mathcal {M}_r \models \Gamma $
at the start of stage s.
$\mathcal {M}_r \models \Gamma $
at the start of stage s.
This concludes the construction of
![]() $(\mathcal {M}_r : r \in R)$
. In the computation of
$(\mathcal {M}_r : r \in R)$
. In the computation of
![]() $\mathcal {M}_r$
for a given
$\mathcal {M}_r$
for a given
![]() $r \in R$
, Case 1 and Case 2 can occur at most once each, as observed in the discussion of Case 2 above. Therefore elements are added to
$r \in R$
, Case 1 and Case 2 can occur at most once each, as observed in the discussion of Case 2 above. Therefore elements are added to
![]() $\mathcal {M}_r$
at most twice, so it is finite. It also follows that
$\mathcal {M}_r$
at most twice, so it is finite. It also follows that
![]() $\mathcal {M}_r \models \Gamma $
at the end of the construction because
$\mathcal {M}_r \models \Gamma $
at the end of the construction because
![]() $\mathcal {M}_r \models \Gamma $
at every stage.
$\mathcal {M}_r \models \Gamma $
at every stage.
We show that the above items (1)–(3) hold.
For item (1), consider a
![]() $k \in X$
. If
$k \in X$
. If
![]() $k = k_0$
, then
$k = k_0$
, then
![]() $|M_r| = k$
whenever
$|M_r| = k$
whenever
![]() $r \in R$
and
$r \in R$
and
![]() $F(r) = k$
. Suppose instead that
$F(r) = k$
. Suppose instead that
![]() $k> k_0$
. Both
$k> k_0$
. Both
![]() $\exists a\, \forall b\, P(k, a, b)$
and
$\exists a\, \forall b\, P(k, a, b)$
and
![]() $\forall a\, \exists b\, Q(k, a, b)$
hold because
$\forall a\, \exists b\, Q(k, a, b)$
hold because
![]() $k \in X$
. Suppose that
$k \in X$
. Suppose that
![]() $r \in R$
has
$r \in R$
has
![]() $F(r) = k$
and is large enough so that
$F(r) = k$
and is large enough so that
![]() $(\exists a < r)(\forall b)\, P(k, a, b)$
. Then Case 2 never occurs in the computation of
$(\exists a < r)(\forall b)\, P(k, a, b)$
. Then Case 2 never occurs in the computation of
![]() $\mathcal {M}_r$
because
$\mathcal {M}_r$
because
![]() $(\forall a < r)(\exists b < s)\, \neg P(F(r), a, b)$
always fails. On the other hand, Case 1 occurs at the first stage s such that
$(\forall a < r)(\exists b < s)\, \neg P(F(r), a, b)$
always fails. On the other hand, Case 1 occurs at the first stage s such that
![]() $(\forall a < r)(\exists b < s)\, Q(F(r), a, b)$
. Therefore
$(\forall a < r)(\exists b < s)\, Q(F(r), a, b)$
. Therefore
![]() $|M_r| = k$
. This shows that
$|M_r| = k$
. This shows that
![]() $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k)$
.
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k)$
.
For item (2), consider a
![]() $k < k_0$
. Then
$k < k_0$
. Then
![]() $|M_r| = r+1$
whenever
$|M_r| = r+1$
whenever
![]() $r \in R$
,
$r \in R$
,
![]() $r \geq k_0$
, and
$r \geq k_0$
, and
![]() $F(r) = k$
. Thus
$F(r) = k$
. Thus
![]() $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
.
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
.
For item (3), consider a
![]() $k> k_0$
with
$k> k_0$
with
![]() $k \notin X$
. Then either
$k \notin X$
. Then either
![]() $\forall a\, \exists b\, \neg P(k, a, b)$
or
$\forall a\, \exists b\, \neg P(k, a, b)$
or
![]() $\exists a\, \forall b\, \neg Q(k, a, b)$
. First suppose that
$\exists a\, \forall b\, \neg Q(k, a, b)$
. First suppose that
![]() $\forall a\, \exists b\, \neg P(k, a, b)$
holds. Let
$\forall a\, \exists b\, \neg P(k, a, b)$
holds. Let
![]() $r \in R$
have
$r \in R$
have
![]() $F(r) = k$
and
$F(r) = k$
and
![]() $r \geq k$
. Let s be the first stage at which
$r \geq k$
. Let s be the first stage at which
![]() $(\forall a < r)(\exists b < s)\, \neg P(F(r), a, b)$
in the computation of
$(\forall a < r)(\exists b < s)\, \neg P(F(r), a, b)$
in the computation of
![]() $\mathcal {M}_r$
. Then
$\mathcal {M}_r$
. Then
![]() $|M_r| \leq r$
at the beginning of stage s. This is because Case 2 cannot have occurred before stage s by the choice of s, so either
$|M_r| \leq r$
at the beginning of stage s. This is because Case 2 cannot have occurred before stage s by the choice of s, so either
![]() $|M_r| = k_0 < r$
(if Case 1 has not occurred by stage s) or
$|M_r| = k_0 < r$
(if Case 1 has not occurred by stage s) or
![]() $|M_r| = k \leq r$
(if Case 1 has occurred by stage s). Thus Case 2 occurs at stage s, so
$|M_r| = k \leq r$
(if Case 1 has occurred by stage s). Thus Case 2 occurs at stage s, so
![]() $|M_r| = r+1$
at the end of stage s. Neither Case 1 nor Case 2 occurs after stage s because Case 2 occurs at most once and Case 1 cannot occur after Case 2. Thus
$|M_r| = r+1$
at the end of stage s. Neither Case 1 nor Case 2 occurs after stage s because Case 2 occurs at most once and Case 1 cannot occur after Case 2. Thus
![]() $|M_r| = r+1$
at the end of the construction. This shows that
$|M_r| = r+1$
at the end of the construction. This shows that
![]() $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
.
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
.
Finally, suppose that
![]() $\exists a\, \forall b\, \neg Q(k, a, b)$
holds but
$\exists a\, \forall b\, \neg Q(k, a, b)$
holds but
![]() $\forall a\, \exists b\, \neg P(k, a, b)$
fails. Thus both
$\forall a\, \exists b\, \neg P(k, a, b)$
fails. Thus both
![]() $\exists a\, \forall b\, P(k, a, b)$
and
$\exists a\, \forall b\, P(k, a, b)$
and
![]() $\exists a\, \forall b\, \neg Q(k, a, b)$
hold. Suppose that
$\exists a\, \forall b\, \neg Q(k, a, b)$
hold. Suppose that
![]() $r \in R$
has
$r \in R$
has
![]() $F(r) = k$
and is large enough so that
$F(r) = k$
and is large enough so that
![]() $(\exists a < r)(\forall b)\, P(F(r), a, b)$
and
$(\exists a < r)(\forall b)\, P(F(r), a, b)$
and
![]() $(\exists a < r)(\forall b)\, \neg Q(F(r), a, b)$
. Then neither Case 1 nor Case 2 occur at any stage in the computation of
$(\exists a < r)(\forall b)\, \neg Q(F(r), a, b)$
. Then neither Case 1 nor Case 2 occur at any stage in the computation of
![]() $\mathcal {M}_r$
. Thus
$\mathcal {M}_r$
. Thus
![]() $|M_r| = k_0$
. This shows that
$|M_r| = k_0$
. This shows that
![]() $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k_0)$
and completes the argument that item (3) holds.
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k_0)$
and completes the argument that item (3) holds.
Let
![]() $\mathcal {L}$
be the generalized sum
$\mathcal {L}$
be the generalized sum
![]() $\sum _{r \in R} (\mathcal {M}_r {\restriction } {\prec })$
of the sequence
$\sum _{r \in R} (\mathcal {M}_r {\restriction } {\prec })$
of the sequence
![]() $(\mathcal {M}_r : r \in R)$
, viewed as a sequence of finite linear orders, over the linear order
$(\mathcal {M}_r : r \in R)$
, viewed as a sequence of finite linear orders, over the linear order
![]() $\mathcal {R}$
as indicated above. Then
$\mathcal {R}$
as indicated above. Then
![]() $\mathcal {L}$
is a computable copy of
$\mathcal {L}$
is a computable copy of
![]() $\omega $
. Let C be a cohesive set for which
$\omega $
. Let C be a cohesive set for which
![]() $\prod _C \mathcal {O}$
is colorful. We need to show that
$\prod _C \mathcal {O}$
is colorful. We need to show that
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
.
$\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
.
Theorem 6.3 gives us that, as linear orders,
 $$ \begin{align*} \prod\nolimits_C \mathcal{L} \quad=\quad \prod\nolimits_C \sum_{r \in R}\mathcal{M}_r \quad\cong\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|}\prod\nolimits_C \mathcal{M}_{\theta(n)}. \end{align*} $$
$$ \begin{align*} \prod\nolimits_C \mathcal{L} \quad=\quad \prod\nolimits_C \sum_{r \in R}\mathcal{M}_r \quad\cong\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|}\prod\nolimits_C \mathcal{M}_{\theta(n)}. \end{align*} $$
As in the proofs of Lemmas 6.5 and 6.7, let
![]() $\mathcal {Z}$
denote the linear order
$\mathcal {Z}$
denote the linear order
![]() $\sum _{[\theta ] \in \left |\prod _C \mathcal {R}\right |}\prod _C \mathcal {M}_{\theta (n)}$
; let
$\sum _{[\theta ] \in \left |\prod _C \mathcal {R}\right |}\prod _C \mathcal {M}_{\theta (n)}$
; let
![]() $|\prod _C \mathcal {R}|_{\mathrm {std}}$
and
$|\prod _C \mathcal {R}|_{\mathrm {std}}$
and
![]() $|\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
denote the standard and non-standard parts of
$|\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
denote the standard and non-standard parts of
![]() $\prod _C \mathcal {R}$
; and let
$\prod _C \mathcal {R}$
; and let
 $$ \begin{align*} \mathcal{Z}_{\mathrm{std}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{std}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \\ \mathcal{Z}_{\mathrm{nonstd}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{nonstd}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \end{align*} $$
$$ \begin{align*} \mathcal{Z}_{\mathrm{std}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{std}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \\ \mathcal{Z}_{\mathrm{nonstd}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{nonstd}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \end{align*} $$
so that
![]() $\mathcal {Z} \cong \mathcal {Z}_{\mathrm {std}} + \mathcal {Z}_{\mathrm {nonstd}}$
. We show that the order-type of the block
$\mathcal {Z} \cong \mathcal {Z}_{\mathrm {std}} + \mathcal {Z}_{\mathrm {nonstd}}$
. We show that the order-type of the block
![]() $\prod _C \mathcal {M}_{\theta (n)}$
of
$\prod _C \mathcal {M}_{\theta (n)}$
of
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}})$
corresponding to
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}})$
corresponding to
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
is determined by the color
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
is determined by the color
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
of
$F^{\prod _C \mathcal {O}}([\theta ])$
of
![]() $[\theta ]$
in
$[\theta ]$
in
![]() $\prod _C \mathcal {O}$
.
$\prod _C \mathcal {O}$
.
Claim 1. If
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
and
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
and
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
is solid color
$F^{\prod _C \mathcal {O}}([\theta ])$
is solid color
![]() for a
for a
![]() $k \in X$
, then
$k \in X$
, then
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
as a linear order.
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
as a linear order.
Proof of Claim 1
We have that
![]() $\lim _{n \in C} \theta (n) = \infty $
by Lemma 4.2 and that
$\lim _{n \in C} \theta (n) = \infty $
by Lemma 4.2 and that
![]() $(\forall ^\infty n \in C)(F(\theta (n)) = k)$
by definition. Furthermore,
$(\forall ^\infty n \in C)(F(\theta (n)) = k)$
by definition. Furthermore,
![]() $k \in X$
implies that
$k \in X$
implies that
![]() $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k)$
by item (1). Therefore
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k)$
by item (1). Therefore
![]() $(\forall ^\infty n \in C)(|M_{\theta (n)}| = k)$
. Thus
$(\forall ^\infty n \in C)(|M_{\theta (n)}| = k)$
. Thus
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
by Lemma 6.4.
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
by Lemma 6.4.
Claim 2. If
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
and
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
and
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
is solid color
$F^{\prod _C \mathcal {O}}([\theta ])$
is solid color
![]() with
with
![]() $k < k_0$
, then
$k < k_0$
, then
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
as a linear order.
$\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
as a linear order.
Proof of Claim 2
Again,
![]() $\lim _{n \in C} \theta (n) = \infty $
by Lemma 4.2 and
$\lim _{n \in C} \theta (n) = \infty $
by Lemma 4.2 and
![]() $(\forall ^\infty n \in C)(F(\theta (n)) = k)$
by definition. Furthermore,
$(\forall ^\infty n \in C)(F(\theta (n)) = k)$
by definition. Furthermore,
![]() $k < k_0$
implies that
$k < k_0$
implies that
![]() $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
by item (2). Therefore
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
by item (2). Therefore
![]() $\lim _{n \in C}|M_{\theta (n)}| = \infty $
, so
$\lim _{n \in C}|M_{\theta (n)}| = \infty $
, so
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
by Lemma 6.6.
$\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
by Lemma 6.6.
Claim 3. If
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
and
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
and
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
is solid color
$F^{\prod _C \mathcal {O}}([\theta ])$
is solid color
![]() for a
for a
![]() $k> k_0$
with
$k> k_0$
with
![]() $k \notin X$
, then, as a linear order,
$k \notin X$
, then, as a linear order,
![]() $\prod _C \mathcal {M}_{\theta (n)}$
either has type
$\prod _C \mathcal {M}_{\theta (n)}$
either has type
![]() $\boldsymbol {k}_0$
or type
$\boldsymbol {k}_0$
or type
![]() $\omega + \zeta \eta + \omega ^*$
.
$\omega + \zeta \eta + \omega ^*$
.
Proof of Claim 3
Again,
![]() $\lim _{n \in C} \theta (n) = \infty $
by Lemma 4.2 and
$\lim _{n \in C} \theta (n) = \infty $
by Lemma 4.2 and
![]() $(\forall ^\infty n \in C)(F(\theta (n)) = k)$
by definition. As
$(\forall ^\infty n \in C)(F(\theta (n)) = k)$
by definition. As
![]() $k> k_0$
and
$k> k_0$
and
![]() $k \notin X$
, either
$k \notin X$
, either
![]() $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k_0)$
or
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = k_0)$
or
![]() $(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
by item (3). The first alternative yields that
$(\forall ^\infty r \in R)(F(r) = k \;\rightarrow \; |M_r| = r+1)$
by item (3). The first alternative yields that
![]() $(\forall ^\infty n \in C)(|M_{\theta (n)}| = k_0)$
and hence that
$(\forall ^\infty n \in C)(|M_{\theta (n)}| = k_0)$
and hence that
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_0$
by Lemma 6.4. The second alternative yields that
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_0$
by Lemma 6.4. The second alternative yields that
![]() $\lim _{n \in C}|M_{\theta (n)}| = \infty $
and hence that
$\lim _{n \in C}|M_{\theta (n)}| = \infty $
and hence that
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
by Lemma 6.6.
$\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
by Lemma 6.6.
Claim 4. If
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
and
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
and
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
is a striped color, then, as a linear order,
$F^{\prod _C \mathcal {O}}([\theta ])$
is a striped color, then, as a linear order,
![]() $\prod _C \mathcal {M}_{\theta (n)}$
has either type
$\prod _C \mathcal {M}_{\theta (n)}$
has either type
![]() $\boldsymbol {k}_0$
or type
$\boldsymbol {k}_0$
or type
![]() $\omega + \zeta \eta + \omega ^*$
.
$\omega + \zeta \eta + \omega ^*$
.
Proof of Claim 4
We have that
![]() $\lim _{n \in C} \theta (n) = \infty $
by Lemma 4.2 and that
$\lim _{n \in C} \theta (n) = \infty $
by Lemma 4.2 and that
![]() $\lim _{n \in C} F(\theta (n)) = \infty $
because
$\lim _{n \in C} F(\theta (n)) = \infty $
because
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
is a striped color. By inspecting the construction, we see that for
$F^{\prod _C \mathcal {O}}([\theta ])$
is a striped color. By inspecting the construction, we see that for
![]() $r \in R$
, either
$r \in R$
, either
![]() $|M_r| = k_0$
,
$|M_r| = k_0$
,
![]() $|M_r| = F(r)$
, or
$|M_r| = F(r)$
, or
![]() $|M_r| = r+1$
. By cohesiveness, either
$|M_r| = r+1$
. By cohesiveness, either
![]() $(\forall ^\infty n \in C)(|M_{\theta (n)}| \leq k_0)$
or
$(\forall ^\infty n \in C)(|M_{\theta (n)}| \leq k_0)$
or
![]() $(\forall ^\infty n \in C)(|M_{\theta (n)}|> k_0)$
. If
$(\forall ^\infty n \in C)(|M_{\theta (n)}|> k_0)$
. If
![]() $(\forall ^\infty n \in C)(|M_{\theta (n)}| \leq k_0)$
, then in fact
$(\forall ^\infty n \in C)(|M_{\theta (n)}| \leq k_0)$
, then in fact
![]() $(\forall ^\infty n \in C)(|M_{\theta (n)}| = k_0)$
because
$(\forall ^\infty n \in C)(|M_{\theta (n)}| = k_0)$
because
![]() $\lim _{n \in C} F(\theta (n)) = \infty $
. In this case, we have that
$\lim _{n \in C} F(\theta (n)) = \infty $
. In this case, we have that
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_0$
by Lemma 6.4. If instead
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}_0$
by Lemma 6.4. If instead
![]() $(\forall ^\infty n \in C)(|M_{\theta (n)}|> k_0)$
, then it must be that
$(\forall ^\infty n \in C)(|M_{\theta (n)}|> k_0)$
, then it must be that
![]() $\lim _{n \in C}|M_{\theta (n)}| = \infty $
. This is because
$\lim _{n \in C}|M_{\theta (n)}| = \infty $
. This is because
![]() $|M_{\theta (n)}|$
is either
$|M_{\theta (n)}|$
is either
![]() $F(\theta (n))$
or
$F(\theta (n))$
or
![]() $\theta (n) + 1$
for almost every
$\theta (n) + 1$
for almost every
![]() $n \in C$
, and both
$n \in C$
, and both
![]() $\lim _{n \in C} F(\theta (n)) = \infty $
and
$\lim _{n \in C} F(\theta (n)) = \infty $
and
![]() $\lim _{n \in C} \theta (n) = \infty $
. Therefore
$\lim _{n \in C} \theta (n) = \infty $
. Therefore
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
by Lemma 6.6.
$\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
by Lemma 6.6.
If
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {std}}$
, then there is an
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {std}}$
, then there is an
![]() $r \in R$
such that
$r \in R$
such that
![]() $(\forall ^\infty n \in C)(\theta (n) = r)$
. Therefore there is a
$(\forall ^\infty n \in C)(\theta (n) = r)$
. Therefore there is a
![]() $k> 0$
such that
$k> 0$
such that
![]() $(\forall ^\infty n \in C)(|M_{\theta (n)}| = k)$
, in which case
$(\forall ^\infty n \in C)(|M_{\theta (n)}| = k)$
, in which case
![]() $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
by Lemma 6.4. This means that
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
by Lemma 6.4. This means that
![]() $\mathcal {Z}_{\mathrm {std}}$
is a generalized sum of finite linear orders over the copy
$\mathcal {Z}_{\mathrm {std}}$
is a generalized sum of finite linear orders over the copy
![]() $|\prod _C \mathcal {R}|_{\mathrm {std}}$
of
$|\prod _C \mathcal {R}|_{\mathrm {std}}$
of
![]() $\omega $
, so
$\omega $
, so
![]() $\mathcal {Z}_{\mathrm {std}} \cong \omega $
.
$\mathcal {Z}_{\mathrm {std}} \cong \omega $
.
Think of the sum condensation
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}})$
as being colored by
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}})$
as being colored by
![]() $F^{\prod _C \mathcal {O}}$
, where the block
$F^{\prod _C \mathcal {O}}$
, where the block
![]() $\prod _C \mathcal {M}_{\theta (n)}$
corresponding to
$\prod _C \mathcal {M}_{\theta (n)}$
corresponding to
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
gets color
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
gets color
![]() $F^{\prod _C \mathcal {O}}([\theta ])$
. The product
$F^{\prod _C \mathcal {O}}([\theta ])$
. The product
![]() $\prod _C \mathcal {O}$
is colorful, which means that
$\prod _C \mathcal {O}$
is colorful, which means that
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}}) \cong |\prod _C \mathcal {R}|_{\mathrm {nonstd}} \cong \eta $
and that each solid color occurs densely. By Claims 1–4 the order-type of block
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}}) \cong |\prod _C \mathcal {R}|_{\mathrm {nonstd}} \cong \eta $
and that each solid color occurs densely. By Claims 1–4 the order-type of block
![]() $\prod _C \mathcal {M}_{\theta (n)}$
for
$\prod _C \mathcal {M}_{\theta (n)}$
for
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
is:
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
is:
-
•
 $\boldsymbol {k}$
if
$\boldsymbol {k}$
if
 $[\theta ]$
has solid color
$[\theta ]$
has solid color
 with
with
 $k \in X$
.
$k \in X$
. -
•
 $\omega + \zeta \eta + \omega ^*$
if
$\omega + \zeta \eta + \omega ^*$
if
 $[\theta ]$
has solid color
$[\theta ]$
has solid color
 with
with
 $k < k_0$
(which includes
$k < k_0$
(which includes
 $k = 0$
because
$k = 0$
because
 $k_0> 0$
).
$k_0> 0$
). -
• Either
 $\boldsymbol {k}_0$
or
$\boldsymbol {k}_0$
or
 $\omega + \zeta \eta + \omega ^*$
if
$\omega + \zeta \eta + \omega ^*$
if
 $[\theta ]$
has solid color
$[\theta ]$
has solid color
 with
with
 $k> k_0$
and
$k> k_0$
and
 $k \notin X$
.
$k \notin X$
. -
• Either
 $\boldsymbol {k}_0$
or
$\boldsymbol {k}_0$
or
 $\omega + \zeta \eta + \omega ^*$
if
$\omega + \zeta \eta + \omega ^*$
if
 $[\theta ]$
has a striped color.
$[\theta ]$
has a striped color.
Therefore
![]() $\mathcal {Z}_{\mathrm {nonstd}} \;\cong \; \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. Thus
$\mathcal {Z}_{\mathrm {nonstd}} \;\cong \; \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. Thus
as desired.
Lemma 6.9. Let
![]() $X \subseteq \mathbb {N} \setminus \{0\}$
be a Boolean combination of
$X \subseteq \mathbb {N} \setminus \{0\}$
be a Boolean combination of
![]() $\Sigma _2$
sets, thought of as a set of finite order-types. Let
$\Sigma _2$
sets, thought of as a set of finite order-types. Let
![]() $\mathcal {O}$
be a computable colored copy of
$\mathcal {O}$
be a computable colored copy of
![]() $\omega $
. There is a computable copy
$\omega $
. There is a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
(constructed from
$\omega $
(constructed from
![]() $\mathcal {O}$
) such that for every cohesive set C, if
$\mathcal {O}$
) such that for every cohesive set C, if
![]() $\prod _C \mathcal {O}$
is colorful, then
$\prod _C \mathcal {O}$
is colorful, then
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
.
$\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
.
Proof The
![]() $X = \emptyset $
case is Lemma 6.7, so we may assume that
$X = \emptyset $
case is Lemma 6.7, so we may assume that
![]() $X \neq \emptyset $
. Let
$X \neq \emptyset $
. Let
![]() $k_0$
be the least element of X. By putting X in disjunctive normal form and noticing that finite intersections of
$k_0$
be the least element of X. By putting X in disjunctive normal form and noticing that finite intersections of
![]() $\Sigma _2$
sets are
$\Sigma _2$
sets are
![]() $\Sigma _2$
and that finite intersections of
$\Sigma _2$
and that finite intersections of
![]() $\Pi _2$
sets are
$\Pi _2$
sets are
![]() $\Pi _2$
, we may write X as a finite union
$\Pi _2$
, we may write X as a finite union
![]() $X = \bigcup _{i < N} X_i$
, where each
$X = \bigcup _{i < N} X_i$
, where each
![]() $X_i$
is the intersection of a
$X_i$
is the intersection of a
![]() $\Sigma _2$
set and a
$\Sigma _2$
set and a
![]() $\Pi _2$
set. It is convenient to further assume that
$\Pi _2$
set. It is convenient to further assume that
![]() $k_0 \in X_i$
for each
$k_0 \in X_i$
for each
![]() $i < N$
.
$i < N$
.
Let
![]() $\mathcal {O} = (R, \mathbb {N}, \prec _{\mathcal {R}}, G)$
be a computable colored copy of
$\mathcal {O} = (R, \mathbb {N}, \prec _{\mathcal {R}}, G)$
be a computable colored copy of
![]() $\omega $
, and let
$\omega $
, and let
![]() $\mathcal {R}$
denote
$\mathcal {R}$
denote
![]() $(R, \prec _{\mathcal {R}})$
. We define a uniformly computable sequence
$(R, \prec _{\mathcal {R}})$
. We define a uniformly computable sequence
![]() $(\mathcal {M}_r : r \in R)$
of
$(\mathcal {M}_r : r \in R)$
of
![]() $\mathfrak {O}$
-structures that are finite models of
$\mathfrak {O}$
-structures that are finite models of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $\langle \cdot , \cdot \rangle \colon \{0, \dots , N-1\} \times \mathbb {N} \rightarrow \mathbb {N}$
be a computable bijection with computable projections
$\langle \cdot , \cdot \rangle \colon \{0, \dots , N-1\} \times \mathbb {N} \rightarrow \mathbb {N}$
be a computable bijection with computable projections
![]() $\pi _0$
and
$\pi _0$
and
![]() $\pi _1$
. Compute each
$\pi _1$
. Compute each
![]() $\mathcal {M}_r$
as in the proof of Lemma 6.8, but for set
$\mathcal {M}_r$
as in the proof of Lemma 6.8, but for set
![]() $X_{\pi _0(G(r))}$
and color
$X_{\pi _0(G(r))}$
and color
![]() $F(r) = \pi _1(G(r))$
.
$F(r) = \pi _1(G(r))$
.
Let
![]() $\mathcal {L}$
be the generalized sum
$\mathcal {L}$
be the generalized sum
![]() $\sum _{r \in R} \mathcal {M}_r$
, as in the proof of Lemma 6.8. Then
$\sum _{r \in R} \mathcal {M}_r$
, as in the proof of Lemma 6.8. Then
![]() $\mathcal {L}$
is a computable copy of
$\mathcal {L}$
is a computable copy of
![]() $\omega $
. Let C be a cohesive set for which
$\omega $
. Let C be a cohesive set for which
![]() $\prod _C \mathcal {O}$
is colorful. Then again
$\prod _C \mathcal {O}$
is colorful. Then again
![]() $\prod _C \mathcal {L} \;\cong \; \mathcal {Z}_{\mathrm {std}} + \mathcal {Z}_{\mathrm {nonstd}}$
, where
$\prod _C \mathcal {L} \;\cong \; \mathcal {Z}_{\mathrm {std}} + \mathcal {Z}_{\mathrm {nonstd}}$
, where
![]() $|\prod _C \mathcal {R}|_{\mathrm {std}}$
and
$|\prod _C \mathcal {R}|_{\mathrm {std}}$
and
![]() $|\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
denote the standard and non-standard parts of
$|\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
denote the standard and non-standard parts of
![]() $\prod _C \mathcal {R}$
,
$\prod _C \mathcal {R}$
,
 $$ \begin{align*} \mathcal{Z}_{\mathrm{std}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{std}}}\prod\nolimits_C \mathcal{M}_{\theta(n),} \\ \mathcal{Z}_{\mathrm{nonstd}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{nonstd}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \end{align*} $$
$$ \begin{align*} \mathcal{Z}_{\mathrm{std}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{std}}}\prod\nolimits_C \mathcal{M}_{\theta(n),} \\ \mathcal{Z}_{\mathrm{nonstd}} \quad&=\quad \sum_{[\theta] \in \left|\prod_C \mathcal{R}\right|{}_{\mathrm{nonstd}}}\prod\nolimits_C \mathcal{M}_{\theta(n)}, \end{align*} $$
and
![]() $\mathcal {Z}_{\mathrm {std}} \cong \omega $
.
$\mathcal {Z}_{\mathrm {std}} \cong \omega $
.
Again, think of
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}})$
as being colored by
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}})$
as being colored by
![]() $G^{\prod _C \mathcal {O}}$
, where the block
$G^{\prod _C \mathcal {O}}$
, where the block
![]() $\prod _C \mathcal {M}_{\theta (n)}$
corresponding to
$\prod _C \mathcal {M}_{\theta (n)}$
corresponding to
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
gets color
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
gets color
![]() $G^{\prod _C \mathcal {O}}([\theta ])$
. The product
$G^{\prod _C \mathcal {O}}([\theta ])$
. The product
![]() $\prod _C \mathcal {O}$
is colorful, which means that
$\prod _C \mathcal {O}$
is colorful, which means that
![]() $\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}}) \cong |\prod _C \mathcal {R}|_{\mathrm {nonstd}} \cong \eta $
and that each solid color occurs densely. The order-type of block
$\operatorname {\mathrm {\mathbf {c}_{\Sigma }}}(\mathcal {Z}_{\mathrm {nonstd}}) \cong |\prod _C \mathcal {R}|_{\mathrm {nonstd}} \cong \eta $
and that each solid color occurs densely. The order-type of block
![]() $\prod _C \mathcal {M}_{\theta (n)}$
for each
$\prod _C \mathcal {M}_{\theta (n)}$
for each
![]() $[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
can be determined as in the proof of Lemma 6.8.
$[\theta ] \in |\prod _C \mathcal {R}|_{\mathrm {nonstd}}$
can be determined as in the proof of Lemma 6.8.
-
• If
 $G^{\prod _C \mathcal {O}}([\theta ])$
is solid color
$G^{\prod _C \mathcal {O}}([\theta ])$
is solid color
 where
where
 $k \in X_i$
, then
$k \in X_i$
, then
 $\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
.
$\prod _C \mathcal {M}_{\theta (n)} \cong \boldsymbol {k}$
. -
• If
 $G^{\prod _C \mathcal {O}}([\theta ])$
is solid color
$G^{\prod _C \mathcal {O}}([\theta ])$
is solid color
 where
where
 $k < k_0$
, then
$k < k_0$
, then
 $\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
.
$\prod _C \mathcal {M}_{\theta (n)} \cong \omega + \zeta \eta + \omega ^*$
. -
• If
 $G^{\prod _C \mathcal {O}}([\theta ])$
is solid color
$G^{\prod _C \mathcal {O}}([\theta ])$
is solid color
 where
where
 $k> k_0$
and
$k> k_0$
and
 $k \notin X_i$
, then
$k \notin X_i$
, then
 $\prod _C \mathcal {M}_{\theta (n)}$
either has order-type
$\prod _C \mathcal {M}_{\theta (n)}$
either has order-type
 $\boldsymbol {k}_0$
or order-type
$\boldsymbol {k}_0$
or order-type
 $\omega + \zeta \eta + \omega ^*$
.
$\omega + \zeta \eta + \omega ^*$
. -
• Suppose that
 $G^{\prod _C \mathcal {O}}([\theta ])$
is a striped color. As
$G^{\prod _C \mathcal {O}}([\theta ])$
is a striped color. As
 $\pi _0(G(r)) < N$
for every
$\pi _0(G(r)) < N$
for every
 $r \in R$
, the cohesiveness of C implies that there is an
$r \in R$
, the cohesiveness of C implies that there is an
 $i < N$
such that
$i < N$
such that
 $(\forall ^\infty n \in C)(\pi _0(G(\theta (n))) = i)$
. Therefore
$(\forall ^\infty n \in C)(\pi _0(G(\theta (n))) = i)$
. Therefore
 $\lim _{n \in C} \pi _1(G(\theta (n))) = \infty $
because
$\lim _{n \in C} \pi _1(G(\theta (n))) = \infty $
because
 $G^{\prod _C \mathcal {O}}([\theta ])$
is striped, and so
$G^{\prod _C \mathcal {O}}([\theta ])$
is striped, and so
 $\prod _C \mathcal {M}_{\theta (n)}$
either has order-type
$\prod _C \mathcal {M}_{\theta (n)}$
either has order-type
 $\boldsymbol {k}_0$
or order-type
$\boldsymbol {k}_0$
or order-type
 $\omega + \zeta \eta + \omega ^*$
as in the proof of Lemma 6.8.
$\omega + \zeta \eta + \omega ^*$
as in the proof of Lemma 6.8.
Therefore
![]() $\mathcal {Z}_{\mathrm {nonstd}} \;\cong \; \boldsymbol {\sigma }(\bigcup _{i < N}X_i \cup \{\omega + \zeta \eta + \omega ^*\}) = \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. Thus
$\mathcal {Z}_{\mathrm {nonstd}} \;\cong \; \boldsymbol {\sigma }(\bigcup _{i < N}X_i \cup \{\omega + \zeta \eta + \omega ^*\}) = \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. Thus
![]() $\prod _C \mathcal {L} \;\cong \; \omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
as desired.
$\prod _C \mathcal {L} \;\cong \; \omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
as desired.
We end with the main result of this section by combining Theorem 5.3 with Lemmas 6.5 and 6.9.
Theorem 6.10. Let
![]() $X \subseteq \mathbb {N} \setminus \{0\}$
be a Boolean combination of
$X \subseteq \mathbb {N} \setminus \{0\}$
be a Boolean combination of
![]() $\Sigma _2$
sets, thought of as a set of finite order-types. Let C be a co-c.e. cohesive set. Then there is a computable copy
$\Sigma _2$
sets, thought of as a set of finite order-types. Let C be a co-c.e. cohesive set. Then there is a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
where the cohesive power
$\omega $
where the cohesive power
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. Moreover, if X is finite and non-empty, then there is also a computable copy
$\omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. Moreover, if X is finite and non-empty, then there is also a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
where the cohesive power
$\omega $
where the cohesive power
![]() $\prod _C \mathcal {L}$
has order-type
$\prod _C \mathcal {L}$
has order-type
![]() $\omega + \boldsymbol {\sigma }(X)$
.
$\omega + \boldsymbol {\sigma }(X)$
.
Proof Let C be a co-c.e. cohesive set. By Theorem 5.3, let
![]() $\mathcal {O}$
be a computable colored copy of
$\mathcal {O}$
be a computable colored copy of
![]() $\omega $
such that
$\omega $
such that
![]() $\prod _C \mathcal {O}$
is colorful. Let
$\prod _C \mathcal {O}$
is colorful. Let
![]() $X \subseteq \mathbb {N} \setminus \{0\}$
be a Boolean combination of
$X \subseteq \mathbb {N} \setminus \{0\}$
be a Boolean combination of
![]() $\Sigma _2$
sets. Let
$\Sigma _2$
sets. Let
![]() $\mathcal {L}$
be the computable copy of
$\mathcal {L}$
be the computable copy of
![]() $\omega $
constructed from
$\omega $
constructed from
![]() $\mathcal {O}$
for X as provided by Lemma 6.9. Then
$\mathcal {O}$
for X as provided by Lemma 6.9. Then
![]() $\prod _C \mathcal {L} \;\cong \; \omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. If X is finite and non-empty, then we may alternatively apply Lemma 6.5 instead of Lemma 6.9 to obtain a computable copy
$\prod _C \mathcal {L} \;\cong \; \omega + \boldsymbol {\sigma }(X \cup \{\omega + \zeta \eta + \omega ^*\})$
. If X is finite and non-empty, then we may alternatively apply Lemma 6.5 instead of Lemma 6.9 to obtain a computable copy
![]() $\mathcal {L}$
of
$\mathcal {L}$
of
![]() $\omega $
with
$\omega $
with
![]() $\prod _C \mathcal {L} \;\cong \; \omega + \boldsymbol {\sigma }(X)$
.
$\prod _C \mathcal {L} \;\cong \; \omega + \boldsymbol {\sigma }(X)$
.
Acknowledgment
We thank our anonymous reviewers for their many thoughtful suggestions of generalizations and alternative proofs that greatly improved the cohesiveness of this work.
Funding
This project was partially supported by the John Templeton Foundation Grant ID 60842 (Shafer); EPSRC Grant EP/T031476/1 (Shafer); the University of Leeds School of Mathematics Research Visitors’ Centre (Dimitrov and Shafer); the FWO Pegasus program (Shafer); FWO/BAS project VS09816 (Shafer and Soskova); BNSF, KP-06-Austria-04/19 (Soskova and Vatev); SU, FNI Grant #80-10-128/16.04.2020 (Soskova and Vatev); NSF FRG Grant DMS-2152095 (Harizanov); Simons Foundation Grant #581896 (Harizanov); Simons Foundation Grant #853762 (Harizanov); and NSF Grant DMS-1600625 (Dimitrov, Harizanov, Morozov, Soskova, and Vatev). The opinions expressed in this work are those of the authors and do not necessarily reflect the views of the John Templeton Foundation.