We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 12 March 2014
In the middle of my Mathematical logic I defined a certain class of formulae as “stratified,” and conjectured that exclusion from this class is a feature “shared, presumably, by all the untenable statements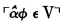 
(p. 157). This ushered in a set of axioms of class-membership which Rosser has since shown to be inconsistent. Accordingly, in Element and number I dropped the principle *200, in which had been assembled axioms to the effect, roughly, that “stratified functions of elements are elements.” In lieu of *200 I set forth alternatives in which no appeal is made to stratification. The system of Mathematical logic exclusive of *200 carries over as an unchanging framework; and this framework admits, we know, of a simple consistency proof. My concern in the present paper is to draw attention to certain relationships between this framework and earlier theories.
1 Rosser, Barkley, The Burali-Forti paradox, this Journal, vol. 7 (1942), pp. 1–17.Google Scholar
2 This Journal, vol. 6 (1941), pp. 135–149.
8 The utility of the stratification concept is not, indeed, quite discredited. The system of my New foundations for mathematical logic (The American mathematical monthly, vol. 44 (1937), pp. 70–80), which uses stratification as a condition of class existence rather than of elementhood, is not yet known to be inconsistent.
4 Cf. Element and number, p. 135.
5 Cf. Mathematical logic p. 161; also D10.
6 Bernays, Paul, A system of axiomatic set theory—Part I, this Journal, vol. 2 (1937), pp. 65–77.Google Scholar
7 Bernays, op. cit., p. 65. Neumann, J. von, Eine Axiomatisierung der Mengenlehre, Journal für die reine und angewandte Mathematik, vol. 154 (1925), pp. 219–240.Google Scholar
8 Not 
because of complications that would arise from the further quantifications which appear within 
when abbreviations are expanded.
9 Cf. Bernays, op. cit., p. 72. He formulates his principle in extension to “κ-tuplets,” but this extension is derivable from the above version.
10 Zermelo, Ernst, Untersuchungen über die Grundlagen der Mengenlehre I, Mathematische Annalen, vol. 65 (1908), pp. 261–281.CrossRefGoogle Scholar
11 Skolem, Thoralf, Einige Bemerkungen zu der Abhandlung von E. Zermelo, Fundamenta mathematicae, vol. 15 (1930), pp. 337–341.CrossRefGoogle Scholar
