Hostname: page-component-76c49bb84f-s7zp8 Total loading time: 0 Render date: 2025-07-07T11:52:49.377Z Has data issue: false hasContentIssue false
  • English
  • Français

ON IDEMPOTENT ULTRAFILTERS IN HIGHER-ORDER REVERSE MATHEMATICS

Published online by Cambridge University Press:  13 March 2015

ALEXANDER P. KREUZER
ALEXANDER P. KREUZER*
Affiliation:
DEPARTMENT OF MATHEMATICS, FACULTY OF SCIENCE, NATIONAL UNIVERSITY OF SINGAPORE, BLOCK S17, 10 LOWER KENT RIDGE ROAD, SINGAPORE 119076, SINGAPOREE-mail: matkaps@nus.edu.sgURL: http://www.math.nus.edu.sg/∼matkaps/
Get access Rights & Permissions [Opens in a new window]

Abstract

We analyze the strength of the existence of idempotent ultrafilters in higher-order reverse mathematics.

Let 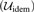$\left( {{{\cal U}_{{\rm{idem}}}}} \right)$ be the statement that an idempotent ultrafilter on ℕ exists. We show that over 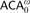$ACA_0^\omega$, the higher-order extension of ACA0, the statement 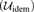$\left( {{{\cal U}_{{\rm{idem}}}}} \right)$ implies the iterated Hindman’s theorem (IHT) and we show that 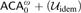$ACA_0^\omega + \left( {{{\cal U}_{{\rm{idem}}}}} \right)$ is 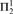${\rm{\Pi }}_2^1$-conservative over 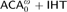$ACA_0^\omega + IHT$ and thus over 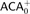$ACA_0^ +$.

Keywords

03B3003F3503F6005D10idempotent ultrafilterHindman’s theoremconservationprogram extractionfunctional interpretationhigher-order reverse mathematics

Information

Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 1 , March 2015 , pp. 179 - 193
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Avigad, Jeremy and Feferman, Solomon, Gödel’s functional (“Dialectica”) interpretation, Handbook of Proof Theory (Buss, S., editor), Studies in Logic and the Foundations of Mathematics, vol. 137, North-Holland, Amsterdam, 1998, pp. 337–405.CrossRefGoogle Scholar
Bergelson, Vitaly, Ergodic Ramsey theory—an update, Ergodic Theory of Zd Actions (Warwick, 1993–1994), London Mathematical Society, Lecture Notes series, vol. 228, Cambridge University Press, Cambridge, 1996, pp. 1–61.Google Scholar
Bergelson, Vitaly, Ultrafilters, IP sets, dynamics, and combinatorial number theory, Ultrafilters Across Mathematics, Contemporary Mathematics, vol. 530, American Mathematical Society, Providence, RI, 2010, pp. 23–47.Google Scholar
Bergelson, Vitaly and Hindman, Neil, Additive and multiplicative Ramsey theorems in N—some elementary results. Combinatorics, Probability and Computing, vol. 2 (1993), no. 3, pp. 221–241.Google Scholar
Bergelson, Vitaly and Tao, Terence, Multiple recurrence in quasirandom groups. Geometric and Functional Analysis, vol. 24 (2014), no. 1, pp. 1–48.Google Scholar
Blass, Andreas, Ultrafilters related to Hindman’s finite-unions theorem and its extensions, Logic and Combinatorics (Arcata, Calif., 1985), Contemporary Mathematics, vol. 65, American Mathematical Society, Providence, RI, 1987, pp. 89–124.Google Scholar
Blass, Andreas and Hindman, Neil, On strongly summable ultrafilters and union ultrafilters. Transactions of the American Mathmatical Society, vol. 30 (1987), no. 1, pp. 83–97.CrossRefGoogle Scholar
Blass, Andreas R., Hirst, Jeffry L., and Simpson, Stephen G., Logical analysis of some theorems of combinatorics and topological dynamics, Logic and Combinatorics (Arcata, Calif., 1985), Contemporary Mathematics, vol. 65, American Mathematical Society, Providence, RI, 1987, pp. 125–156.Google Scholar
Feferman, Solomon, Theories of finite type related to mathematical practice, Handbook of Mathematical Logic (Barwise, Jon, editor), Studies in Logic and the Foundations of Mathematics, vol. 90, North-Holland, Amsterdam, 1977, pp. 913–971.Google Scholar
Gödel, Kurt, Über eine bisher noch nicht benützte Erweiterung des finiten Standpunktes, Dialectica, vol. 12 (1958), pp. 280–287.CrossRefGoogle Scholar
Hindman, Neil, Finite sums from sequences within cells of a partition of N. Journal of Combinatorial Theory, Series. A, vol. 17 (1974), pp. 1–11.Google Scholar
Hindman, Neil and Strauss, Dona, Algebra in the Stone-Čech compactification, Theory and Applications, Second revised and extended edition, de Gruyter Textbook, Walter de Gruyter & Co., Berlin, 2012.Google Scholar
Hirst, Jeffry L., Hindman’s theorem, ultrafilters, and reverse mathematics, this Journal, vol. 69 (2004), no. 1, pp. 65–72.Google Scholar
Hunter, James, Higher-order Reverse Topology, Ph.D. thesis, University of Wisconsin-Madison, Madison, WI, 2008, http://www.math.wisc.edu/∼lempp/theses/hunter.pdf.Google Scholar
Kleene, Stephen C., Recursive functionals and quantifiers of finite types. I. Transactions of the American Mathematical Society, vol. 91 (1959), pp. 1–52.Google Scholar
Kohlenbach, Ulrich, On the no-counterexample interpretation, this Journal, vol. 64 (1999), no. 4, pp. 1491–1511.Google Scholar
Kohlenbach, Ulrich, Higher order reverse mathematics, Reverse Mathematics 2001, Lecture Notes in Logic, vol. 21, Association of Symbolic Logic, La Jolla, CA, 2005, pp. 281–295.Google Scholar
Kohlenbach, Ulrich, Applied Proof Theory: Proof Interpretations and Their Use in Mathematics, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2008.Google Scholar
Kreuzer, Alexander P., Non-principal ultrafilters, program extraction and higher-order reverse mathematics. Journal of Mathematical Logic, vol. 12 (2012), no. 1, 1250002.Google Scholar
Montalbán, Antonio, Open questions in reverse mathematics. Bulletin of Symbolic Logic, vol. 17 (2011), no. 3, pp. 431–454.Google Scholar
Towsner, Henry, Ultrafilters in reverse mathematics. Journal of Mathematical Logic, vol. 14 (2014), no. 1, p. 1450001 (11 pages).Google Scholar
Troelstra, Anne S. (editor), Metamathematical Investigation of Intuitionistic Arithmetic and Analysis, Lecture Notes in Mathematics, vol. 344, Springer-Verlag, Berlin, 1973.CrossRefGoogle Scholar