Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Tressl, Marcus
2005.
The elementary theory of Dedekind cuts in polynomially bounded structures.
Annals of Pure and Applied Logic,
Vol. 135,
Issue. 1-3,
p.
113.
Dolich, Alfred
Miller, Chris
and
Steinhorn, Charles
2009.
Structures having o-minimal open core.
Transactions of the American Mathematical Society,
Vol. 362,
Issue. 3,
p.
1371.
Fischer, Andreas
2014.
Approximation of o-minimal maps satisfying a Lipschitz condition.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 3,
p.
787.
Dolich, Alfred
Miller, Chris
and
Steinhorn, Charles
2016.
Expansions of o-minimal structures by dense independent sets.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 8,
p.
684.
Peterzil, Yaácov
Speissegger, Patrick
and
Starchenko, Sergei
2017.
Logic Colloquium '98.
p.
357.
Miller, Chris
2017.
Logic Colloquium '01.
p.
281.
Walsberg, Erik
2021.
Externally definable quotients and NIP expansions of the real ordered additive group.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 3,
p.
1551.
Andújar Guerrero, Pablo
Thomas, Margaret E. M.
and
Walsberg, Erik
2021.
Directed sets and topological spaces definable in o‐minimal structures.
Journal of the London Mathematical Society,
Vol. 104,
Issue. 3,
p.
989.
Hieronymi, Philipp
and
Walsberg, Erik
2021.
A tetrachotomy for expansions of the real ordered additive group.
Selecta Mathematica,
Vol. 27,
Issue. 4,
Baizhanov, Bektur
Tazabekova, Nargiza
and
Zambarnaya, Tatyana
2025.
Orthogonality of 1-Types over Sets, Neighborhoods of Sets in 1-Types in Weakly Ordered Minimal Theories.
Mathematics,
Vol. 13,
Issue. 20,
p.
3271.
Baizhanov, B.
Tazabekova, N.
and
Zambarnaya, T.
2025.
NEIGHBORHOODS IN WEAKLY ORDERED MINIMAL THEORIES.
Herald of the Kazakh-British Technical University,
Vol. 22,
Issue. 3,
p.
271.
Baizhanov, Bektur
and
Tazabekova, Nargiza
2025.
Essential kinds of 1-types over sets of models of weakly o-minimal theories.
Kazakh Mathematical Journal,
Vol. 23,
Issue. 4,
p.
6.
SIMON, PIERRE
and
WALSBERG, ERIK
2025.
DP AND OTHER MINIMALITIES.
The Journal of Symbolic Logic,
p.
1.
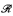 . We then show that a definable function in an o-minimal expansion of
. We then show that a definable function in an o-minimal expansion of 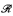 enjoys good differentiability properties and use this to prove that an Archimedean real closed field is definable in any nonsemilinear expansion of
enjoys good differentiability properties and use this to prove that an Archimedean real closed field is definable in any nonsemilinear expansion of 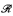 . Combining these results, we obtain several restrictions on possible o-minimal expansions of arbitrary Archimedean ordered groups and in particular of the rational ordered group.
. Combining these results, we obtain several restrictions on possible o-minimal expansions of arbitrary Archimedean ordered groups and in particular of the rational ordered group.
