Article contents
On the category of models of a complete theory
Published online by Cambridge University Press: 12 March 2014
Extract
Let T be a countable complete theory and C(T) the category whose objects are the models of T and morphisms are the elementary maps. The main object of this paper will be the study of C(T). The idea that a better understanding of the category may give us model theoretic information about T is quite natural: The (semi) group of automorphisms (endomorphisms) of a given structure is often a powerful tool for studying this structure. But certainly, one of the very first questions to be answered is: “to what extent does this category C(T) determine T?”
There is some obvious limitation: for example let T0 be the theory of infinite sets (in a language containing only =) and T1 the theory, in the language ( =, U(ν0),f(ν0)) stating that:
(1) U is infinite.
(2)f is a bijective map from U onto its complement.
It is quite easy to see that C(T0) is equivalent to C(T1). But, in this case, T0 andT1 can be “interpreted” each in the other. To make this notion of interpretation precise, we shall associate with each theory T a category, loosely denoted by T, defined as follows:
(1) The objects are the formulas 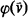 in the given language.
in the given language.
(2) The morphisms from 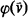 into
into 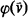 are the formulas
are the formulas 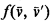 such that
such that
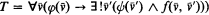
(i.e. f defines a map from ϕ into ϕ; two morphisms defining the same map in all models of T should be identified).
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1982
References
REFERENCES
- 29
- Cited by

