No CrossRef data available.
Article contents
ON THE DECIDABILITY OF THE 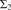 ${{\rm{\Sigma }}_2}$ THEORIES OF THE ARITHMETIC AND HYPERARITHMETIC DEGREES AS UPPERSEMILATTICES
${{\rm{\Sigma }}_2}$ THEORIES OF THE ARITHMETIC AND HYPERARITHMETIC DEGREES AS UPPERSEMILATTICES
Published online by Cambridge University Press: 09 January 2018
Abstract
We establish the decidability of the  ${{\rm{\Sigma }}_2}$ theory of both the arithmetic and hyperarithmetic degrees in the language of uppersemilattices, i.e., the language with ≤, 0 , and
${{\rm{\Sigma }}_2}$ theory of both the arithmetic and hyperarithmetic degrees in the language of uppersemilattices, i.e., the language with ≤, 0 , and  $\sqcup$ . This is achieved by using Kumabe-Slaman forcing, along with other known results, to show given finite uppersemilattices
$\sqcup$ . This is achieved by using Kumabe-Slaman forcing, along with other known results, to show given finite uppersemilattices 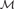 ${\cal M}$ and
${\cal M}$ and 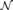 ${\cal N}$ , where
${\cal N}$ , where 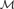 ${\cal M}$ is a subuppersemilattice of
${\cal M}$ is a subuppersemilattice of 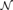 ${\cal N}$ , that every embedding of
${\cal N}$ , that every embedding of 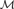 ${\cal M}$ into either degree structure extends to one of
${\cal M}$ into either degree structure extends to one of 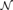 ${\cal N}$ iff
${\cal N}$ iff 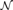 ${\cal N}$ is an end-extension of
${\cal N}$ is an end-extension of 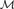 ${\cal M}$ .
${\cal M}$ .
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
Ash, C. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, Elsevier Science, Amsterdam, 2000.Google Scholar
Harrington, L., Shore, R., and Slaman, T.,
 ${\rm{\Sigma }}_1^1$
in every real in a
${\rm{\Sigma }}_1^1$
in every real in a
 ${\rm{\Sigma }}_1^1$
class of reals is
${\rm{\Sigma }}_1^1$
class of reals is
 ${\rm{\Sigma }}_1^1$
, Computability and Complexity, Essays Dedicated to Rodney Downey on the Occasion of his 60th Birthday (Day, A., Felows, M., Greenberg, N., Khoussainov, B., Melnikov, A., and Rosamond, F., editors), Springer-Verlag, Berlin, Heidelberg, 2017, pp. 455–468.Google Scholar
${\rm{\Sigma }}_1^1$
, Computability and Complexity, Essays Dedicated to Rodney Downey on the Occasion of his 60th Birthday (Day, A., Felows, M., Greenberg, N., Khoussainov, B., Melnikov, A., and Rosamond, F., editors), Springer-Verlag, Berlin, Heidelberg, 2017, pp. 455–468.Google Scholar
Jockusch, C. and Slaman, T., On the
 ${{\rm{\Sigma }}_2}$
-theory of the upper semilattice of Turing degrees, this Journal, vol. 58 (1993), no. 1, pp. 193–204.Google Scholar
${{\rm{\Sigma }}_2}$
-theory of the upper semilattice of Turing degrees, this Journal, vol. 58 (1993), no. 1, pp. 193–204.Google Scholar
Kjos-Hanssen, B. and Shore, R., Lattice initial segments of the hyperdegrees, this Journal, vol. 75 (2010).Google Scholar
Lerman, M., Degrees of Unsolvability, Perspectives in Mathematical Logic, Omega Series, Springer-Verlag, Berlin, Heidelberg, New York, Tokyo, 1983.CrossRefGoogle Scholar
Sacks, G., Higher Recursion Theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.CrossRefGoogle Scholar
Shore, R., The Turing Degrees: An Introduction, Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore, 29, World Scientific Publishing, Singapore, 2015, pp. 39–121.Google Scholar
Shore, R. and Slaman, T., Defining the Turing Jump. Mathematical Research Letters, vol. 6 (1999), no. 6, pp. 711–722.Google Scholar
Simpson, M., Arithmetic degrees: Initial segments, ω-REA operators and the ω-jump, Ph.D. thesis, Cornell University, 1985.Google Scholar

