Article contents
On the structure of the Medvedev lattice
Published online by Cambridge University Press: 12 March 2014
Abstract
We investigate the structure of the Medvedev lattice as a partial order. We prove that every interval in the lattice is either finite, in which case it is isomorphic to a finite Boolean algebra, or contains an antichain of size 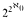 . the size of the lattice itself. We also prove that it is consistent with ZFC that the lattice has chains of size
. the size of the lattice itself. We also prove that it is consistent with ZFC that the lattice has chains of size 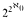 . and in fact that these big chains occur in every infinite interval. We also study embeddings of lattices and algebras. We show that large Boolean algebras can be embedded into the Medvedev lattice as upper semilattices, but that a Boolean algebra can be embedded as a lattice only if it is countable. Finally we discuss which of these results hold for the closely related Muchnik lattice.
. and in fact that these big chains occur in every infinite interval. We also study embeddings of lattices and algebras. We show that large Boolean algebras can be embedded into the Medvedev lattice as upper semilattices, but that a Boolean algebra can be embedded as a lattice only if it is countable. Finally we discuss which of these results hold for the closely related Muchnik lattice.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
REFERENCES
- 3
- Cited by

