Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-30T12:48:31.863Z Has data issue: false hasContentIssue false
  • English
  • Français

Ordinals connected with formal theories for transfinitely iterated inductive definitions

Published online by Cambridge University Press:  12 March 2014

W. Pohlers
W. Pohlers*
Affiliation:
Mathematisches Institut Der Ludwig-Maximilians-Universität, Munchen, Federal Republic of Germany
Get access Rights & Permissions [Opens in a new window]

Extract

Let Th be a formal theory extending number theory. Call an ordinal ξ provable in Th if there is a primitive recursive ordering which can be proved in Th to be a wellordering and whose order type is > ξ. One may define the ordinal ∣ Th ∣ of Th to be the least ordinal which is not provable in Th. By [3] and [12] we get 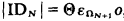, where IDN is the formal theory for N-times iterated inductive definitions. We will generalize this result not only to the case of transfinite iterations but also to a more general notion of ‘the ordinal of a theory’.

For an X-positive arithmetic formula 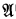[X,x] there is a natural norm ∣x∣: = μξ (x ∈ I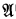ξ), where I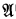ξ is defined as {x: 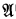[∪μ<ξI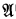μ, x]}by recursion on ξ (cf. [7], [17]). By P 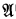we denote the least fixed point of 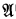[X,x]. Then P 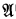= ∪ξ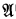ξ holds. If Th allows the formation of P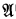, we get the canonical definitions ∥Th(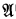)∥ = sup{∣x∣ 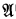+ 1: Th ⊢ x ∈ P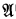} and ∥Th∥ = sup{∥Th(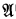)∥: P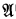 is definable in Th} (cf. [17]). If ≺ is any primitive recursive ordering define Q≺[X,x] as the formula ∀y(y ≺ x → y ∈ X) and ∣x∣≺:= ∣x∣O≺. Then ∣x∣≺ turns out to be the order type of the ≺ -predecessors of x and P 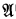is the accessible part of ≺. So Th ⊢ x ∈ P 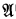implies the provability of ∣x∣≺ in Th.

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 43 , Issue 2 , June 1978 , pp. 161 - 182
Copyright
Copyright © Association for Symbolic Logic 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

BIBLIOGRAPHY

[1]Buchholz, W., Normalfunktionen und konstruktive Systeme von Ordinalzahlen, Proof Theory Symposium, Kiel, 1974, Springer Lecture Notes in Mathematics, 500 (1975), pp. 4-25.Google Scholar
[2]Buchholz, W., Teilsysteme von ({g}), Archiv für mathematische Logik und Grundlagenforschung, vol. 18 (1976), pp. 85–98.CrossRefGoogle Scholar
[3]Buchholz, W. and Pohlers, W., Provable wellorderings of formal theories for transfinitely iterated inductive definitions, this Journal, vol. 43 (1978), pp. 118–125.Google Scholar
[4]Feferman, S., Formal theories for transfinitely iterated inductive definitions, Intuitionism and proof theory (Kino, , Myhill, , Vesley, , Editors), North-Holland, Amsterdam and London, 1970, pp. 303–326.Google Scholar
[5]Gentzen, G., Die Widerspruchsfreiheit der reinen Zahlentheorie, Mathematische Annalen, vol. 112 (1936), pp. 493–565.CrossRefGoogle Scholar
[6]Kino, A., On provable recursive functions and ordinal recursive functions, Journal of the Mathematical Society of Japan, vol. 20 (1968), pp. 456–476.CrossRefGoogle Scholar
[7]Moschovakis, Y. N., Elementary induction on abstract structures, North-Holland, Amsterdam and London, 1974.Google Scholar
[8]Myhill, J., A stumblingblock in constructive mathematics, abstract, this Journal, vol. 18 (1953), pp. 190–191.Google Scholar
[9]Pfeiffer, H.,Ein Bezeichnungssystem für Ordinalzahlen, Archiv für mathematische Logik und Grundlagenforschung, vol. 13 (1970), pp. 74–90.CrossRefGoogle Scholar
[10]Pfeiffer, H., Bezeichnungssysteme für Ordinalzahlen, Communications of the Mathematical Institute, Rijksuniversiteit, Utrecht, 1973.Google Scholar
[11]Pohlers, W., Eine Grenze für die Herleitbarkeit der transfiniten Induktion in einem schwachen Π11-Fragment der Analysis, Dissertation, University of München, 1973.Google Scholar
[12]Pohlers, W., An upper bound for the provability of transfinite induction in systems with N-times iterated inductive definitions, Proof Theory Symposium, Kiel, 1974, Springer Lecture Notes in Mathematics, 500 (1975), pp. 271–289.Google Scholar
[13]Schütte, K., Beweistheorie, Springer-Verlag, Berlin, Göttingen, Heidelberg, 1960.Google Scholar
[14]Schütte, K., Proof theory, Springer-Verlag, Berlin and New York, 1977.CrossRefGoogle Scholar
[15]Shoenfield, J., Mathematical logic, Addison-Wesley, Reading, Massachusetts, 1967.Google Scholar
[16]Takeuti, G., Consistency proofs of subsystems of classical analysis, Annals of Mathematics, vol. 86 (1967), pp. 299–348.CrossRefGoogle Scholar
[17]Zucker, J., Iterated inductive definitions, trees and ordinals, Metamathematical investigations of intuitionistic arithmetic and analysis (Troelstra, , Editor), Springer Lecture Notes in Mathematics, 344 (1973), pp. 392–453.CrossRefGoogle Scholar
[18]Friedman, H., One hundred and two problems in mathematical logic, this Journal, vol. 40 (1975), pp. 113–129.Google Scholar