Hostname: page-component-848d4c4894-p2v8j Total loading time: 0 Render date: 2024-06-08T16:28:58.597Z Has data issue: false hasContentIssue false
  • English
  • Français

Partition properties of M-ultrafilters and ideals

Published online by Cambridge University Press:  12 March 2014

Joji Takahashi
Joji Takahashi*
Affiliation:
Department of Mathematics, University of Papua New Guinea, Port Moresby, Papua New Guinea
*
Faculty of Education, Kobe University, Nada-ku, Kobe 657, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

As is well known, the following are equivalent for any uniform ultrafilter U on an uncountable cardinal:

  • (i) U is selective;

  • (ii) U → ;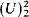

  • (iii) U → .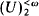

In §1 of this paper, we consider this result in terms of M-ultrafilters (Definition 1.1), where M is a transitive model of ZFC (Zermelo-Fraenkel set theory with the axiom of choice). We define the partition properties and 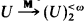for M-ultrafilters (Definition 1.3), and characterize those M-ultrafilters that possess these properties (Theorem 1.5) so that the result mentioned at the beginning is subsumed as the special case that M is V, the universe of all sets. It turns out that the two properties have to be handled separately, and that, besides selectivity, we need to formulate additional conditions (Definition 1.4). The extra conditions become superfluous when M = V because they are then trivially satisfied. One of them is nothing new; it is none other than Kunen's iterability-of-ultrapowers condition.

In §2, we obtain characterizations of the partition properties I+ → 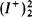and I+ → 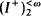(Definition 2.3) of uniform ideals I on an infinite cardinal κ (Theorem 2.6). This is done by applying the main results of §1 to the canonical -ultrafilter in the Boolean-valued model constructed from the completion of the quotient algebra P(κ)/I. They are related to certain known characterizations of weakly compact and of Ramsey cardinals.

Our basic set theory is ZFC. In §1, it has to be supplemented by a new unary predicate symbol M and new nonlogical axioms that make M look like a transitive model of ZFC.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 52 , Issue 4 , December 1987 , pp. 897 - 907
Copyright
Copyright © Association for Symbolic Logic 1987

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BTW]Baumgartner, J. E., Taylor, A. D., and Wagon, S., Structural properties of ideals, Dissertationes Mathematicae (Rozprawy Matematyczne), vol. 197 (1982).Google Scholar
[De]Devlin, K. J., Indescribability properties and small large cardinals, ⊨ ISILC logic conference, Lecture Notes in Mathematics, vol. 499, Springer-Verlag, Berlin, 1975, pp. 89–114.CrossRefGoogle Scholar
[Je]Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[KM]Kanamori, A. and Magidor, M., The evolution of large cardinal axioms in set theory, Higher set theory, Lecture Notes in Mathematics, vol. 669, Springer-Verlag, Berlin, 1978, pp. 99–275.CrossRefGoogle Scholar
[KT]Keisler, H. J. and Tarski, A., From accessible to inaccessible cardinals, Fundamenta Mathematicae, vol. 53 (1964), pp. 225–308.CrossRefGoogle Scholar
[Kl]Kleinberg, E. M., A combinatorial characterization of normal M-ultrafilters, Advances in Mathematics, vol. 30 (1978), pp. 77–84.CrossRefGoogle Scholar
[Ku1]Kunen, K., Some applications of iterated ultrapowers in set theory, Annals of Mathematical Logic, vol. 1 (1970), pp. 179–227.CrossRefGoogle Scholar
[Ku2]Kunen, K., Inaccessibility properties of cardinals, Ph.D. thesis, Stanford University, Stanford, California, 1968.Google Scholar
[Mi]Mitchell, W., Ramsey cardinals and constructibility, this Journal, vol. 44 (1979), pp. 260–266.Google Scholar
[Ro]Rowbottom, F., Some strong axioms of infinity incompatible with the axiom of constructibility, Annals of Mathematical Logic, vol. 3 (1971), pp. 1–44.CrossRefGoogle Scholar