Article contents
Pas d'imaginaires dans l'infini!
Published online by Cambridge University Press: 12 March 2014
Extract
Dans Poizat [1981], le second auteur a montré qu'un sous-groupe infiniment définissable d'un groupe stable était intersection de sous-groupes définissables; il a posé la question de savoir si une relation d'équivalence E, infiniment définissable dans un modèle M d'une théorie stable T, était conjonction de relations d'équivalence définissables. Nous allons voir ici que c'est presque exact: c'est vrai si T est totalement transcendante, et, dans le cas général de stabilité E a toujours un raffinement E1 (plus précisément, E1 est la conjonction de E et de la relation “x et y ont même type”) qui a cette propriété; cela montre que cette relation E n'introduit pas d'imaginaires d'une nature vraiment différente de celle des imaginaires de Shelah: dans une théorie stable, un imaginaire infinitaire n'est rien d'autre qu'un ensemble d'imaginaires finis.
La démonstration du théorème principal de cette note s'appuie lourdement sur la construction Meq de Shelah, la machinerie de la déviation, les paramètres imaginaires canoniques pour la définition d'un type stable, etc…. Pour tout cela, les références adéquates sont Shelah [1978], Pillay [1983], et Poizat [1985, Chapitre 16].
Nouscommençons par préciser ce que nous entendons par “relation d'équivalence infiniment définissable”: une collection de formules e(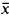 , ȳ),
, ȳ), 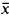 et ȳ étant de longueur n, telle que, pour tout modèle M de T, les couples (
et ȳ étant de longueur n, telle que, pour tout modèle M de T, les couples (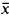 , ȳ) qui les satisfont toutes forment une rélation d'équivalence E.
, ȳ) qui les satisfont toutes forment une rélation d'équivalence E.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1987
References
RÉFÉRENCES
- 9
- Cited by

