Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Troelstra, A.S.
1965.
On Intermediate Propositional Logics.
Indagationes Mathematicae (Proceedings),
Vol. 68,
Issue. ,
p.
141.
Hosoi, Tsutomu
1966.
On the separation theorem of intermediate propositional calculi.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 42,
Issue. 6,
Hosoi, Tsutomu
1966.
The separable axiomatization of the intermediate propositional systems $S_n $ of Gödel.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 42,
Issue. 9,
Hosoi, Tsutomu
1966.
Algebraic proof of the separation theorem on Dummett's $\mathrm{LC}$.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 42,
Issue. 7,
SEGERBERG, KRISTER
1968.
Propositional Logics Related to Heyting's and Johansson's.
Theoria,
Vol. 34,
Issue. 1,
p.
26.
Dunn, J. Michael
and
Meyer, Robert K.
1971.
Algebraic Completeness Results for Dummett's LC and Its Extensions.
Mathematical Logic Quarterly,
Vol. 17,
Issue. 1,
p.
225.
Pahi, Biswambhar
1971.
Full Models and Restricted Extensions of Propositional Calculi.
Mathematical Logic Quarterly,
Vol. 17,
Issue. 1,
p.
5.
Maksimova, L. L.
1972.
Pretabular superintuitionist logic.
Algebra and Logic,
Vol. 11,
Issue. 5,
p.
308.
Graczyńska, Ewa
and
Wroński, Andrzej
1974.
Constructing denumerable matrices strongly adequate for pre-finite logics.
Studia Logica,
Vol. 33,
Issue. 4,
p.
417.
1974.
An Algebraic Approach to Non-Classical Logics.
Vol. 78,
Issue. ,
p.
380.
Epstein, George
and
Horn, Alfred
1976.
Logics Which Are Characterized by Subresiduated Lattices.
Mathematical Logic Quarterly,
Vol. 22,
Issue. 1,
p.
199.
Baker, Kirby A.
1976.
Equational axions for classes of Heyting algebras.
Algebra Universalis,
Vol. 6,
Issue. 1,
p.
105.
Wolf, Robert G.
1977.
Modern Uses of Multiple-Valued Logic.
p.
167.
Gaines, B.R.
and
Kohout, L.J.
1977.
The fuzzy decade: a bibliography of fuzzy systems and closely related topics.
International Journal of Man-Machine Studies,
Vol. 9,
Issue. 1,
p.
1.
Maksimova, L. L.
1977.
Craig's theorem in superintuitionistic logics and amalgamable varieties of pseudo-boolean algebras.
Algebra and Logic,
Vol. 16,
Issue. 6,
p.
427.
Kubin, Wilhelm
1979.
Eine Axiomatisierung der Mehrwertigen Logiken von Gödel.
Mathematical Logic Quarterly,
Vol. 25,
Issue. 33,
p.
549.
Visser, Albert
1981.
A propositional logic with explicit fixed points.
Studia Logica,
Vol. 40,
Issue. 2,
p.
155.
Kabziński, Jacek K.
1982.
Basic properties of the equivalence.
Studia Logica,
Vol. 41,
Issue. 1,
p.
17.
1984.
Topoi - The Categorial Analysis of Logic.
Vol. 98,
Issue. ,
p.
521.
Boričić, Branislav R.
1985.
On Some Subsystems of Dummett's LC.
Mathematical Logic Quarterly,
Vol. 31,
Issue. 14-18,
p.
243.

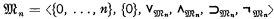 , where
, where