Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-19T03:07:26.516Z Has data issue: false hasContentIssue false
  • English
  • Français

Questions of decidability and undecidability in Number Theory

Published online by Cambridge University Press:  12 March 2014

B. Mazur
B. Mazur*
Affiliation:
Department of Mathematics, Harvard University, Cambridge, Massachusetts 02138, E-mail: mazur@math.harvard.edu
Get access Rights & Permissions [Opens in a new window]

Extract

Davis, Matijasevic, and Robinson, in their admirable survey article [D-M-R], interpret the negative solution of Hilbert's Tenth Problem as a resounding positive statement about the versatility of Diophantine equations (that any listable set can be coded as the set of parameter values for which a suitable polynomial possesses integral solutions).

One can also view the Matijasevic result as implying that there are families of Diophantine equations parametrized by a variable t, which have integral solutions for some integral values t = a > 0, and yet there is no computable function of t which provides an upper bound for the smallest integral solution for these values a. The smallest integral solutions of the Diophantine equation for these values are, at least sporadically, too large to be bounded by any computable function. This is somewhat difficult to visualize, since there is quite an array of computable functions. But let us take an explicit example. Consider the function

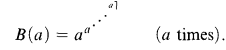
Matijasevic's result guarantees the existence of parametrized families of Diophantine equations such that even this function fails to yield an upper bound for its smallest integral solutions (for all values of the parameter t for which there are integral solutions).

Families of Diophantine equations in a parameter t, whose integral solutions for t = 1, 2, 3,… exhibit a certain arythmia in terms of their size, have fascinated mathematicians for centuries, and this phenomenon (the size of smallest integral solution varying wildly with the parameter-value) is surprising, even when the equations are perfectly “decidable”.

Type
Survey/expository paper
Information
The Journal of Symbolic Logic , Volume 59 , Issue 2 , June 1994 , pp. 353 - 371
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Ba] Baker, A., Transcendental number theory, Cambridge University Press, London and New York, 1975.Google Scholar
[Bu] Büchi, J. R., The collected works of J. Richard Büchi (Maclane, S. and Siefkes, Dirk), editors Springer Verlag, New York, 1990.Google Scholar
[C] Clemens, H., Homological equivalence modulo algebraic equivalence is not finitely generated, Institutdes Hautes Études Scientifiques, Publications Mathématiques,, vol. 58 (1983>, pp. 19–38.Google Scholar
[C-O-G-P] Candelas, P., De La Ossa, X., Green, P., and Parkes, L., A pair of Calabi-Yau manifolds as an exactly soluble superconformal theory, Nuclear Physics B, vol. 359 (1991), pp. 21–74.Google Scholar
[C-V] Conn, W. and Vaserstein, L., On sums of three integral cubes, preprint.Google Scholar
[D-M-R] Davis, M., Matijasevic, Y., and Robinson, J., Diophantine equations: Positive aspects of a negative solution, Proceedings of Symposia in Pure Mathematics, vol. 28 American Mathematical Society, Providence, Rhode Island, (1976), pp. 323–378.Google Scholar
[De1] Denef, J., Hilbert's tenth problem for quadratic rings, Proceedings of the American Mathematical Society, vol. 48 (1975>, pp. 214–220.Google Scholar
[De2] Denef, J., Diophantine sets over algebraic integer rings II, Transactions of the American Mathematical Society, vol. 257 (1980), pp. 227–336.CrossRefGoogle Scholar
[De-Li] Denef, J. and Lipschitz, L., Diophantine sets over some rings of algebraic integers, Journal of the London Mathematical Society, vol. 18 (1978), pp. 385–391.Google Scholar
[E-S] Ellingsrud, G. and Stromme, S., The number of twisted cubics on the general quintic threefold, Essays on mirror manifolds (Yau, S. T., editor), International Press, Hong Kong, (1992), pp. 181–240.Google Scholar
[F1] Faltings, G., Diophantine approximation on abelian varieties, Annals of Mathematics, vol. 133 (1991), pp. 549–576.Google Scholar
[F2] Faltings, G., The general case of S. Lang's conjecture (to appear).Google Scholar
[F-M-T] Franks, J., Manin, Y., and Tschinkel, Y., Rational points of bounded height on Fano varieties, Inventiones Mathematicae, vol. 95 (1989), pp. 421–435.Google Scholar
[F-W] Flath, D. and Wagon, S., How to pick out the integers in the rationals: An application of number theory to logic, American Mathematical Monthly, vol. 98 (1991), pp. 1–5.Google Scholar
[G-L-S] Gardner, V., Lazarus, R., and Stein, P., Solutions of the diophantine equation x3 + y3 = z3 − d, Mathematics of Computation, vol. 18 (1964), pp. 408–413.Google Scholar
[Hua] Hua, L. KI., On the least solution of Pell's equation, Bulletin of the American Mathematical Society, vol. 48 (1942), pp. 731–735.Google Scholar
[J-M] Jones, J. and Matijasevic, Y., Proof of the recursive unsolvability of Hilbert's tenth problem, American Mathematical Monthly, vol. 98 (1991), pp. 689–709.Google Scholar
[K] Katz, S., On the finiteness of rational curves on quintic threefolds, Compositio Mathematica, vol. 60 (1986), pp. 151–162.Google Scholar
[K-O] Kobayashi, S. and Ochiaia, T., Meromorphic mappings into compact spaces of general type, Inventiones Mathematicae, vol. 31 (1975), pp. 7–16.Google Scholar
[L1] Lang, S., Higher dimensional diophantine problems, Bulletin of the American Mathematical Society, vol. 80 (1974), pp. 779–787.Google Scholar
[L2] Lang, S., Elliptic curves: Diophaantine analysis, Springer-Verlag, New York, 1978.Google Scholar
[L3] Lang, S., Hyperbolic and Diophantine analysis, Bulletin of the American Mathematical Society, vol. 14 (1986), pp. 159–205.Google Scholar
[L4] Lang, S., Introduction to complex hyperbolic spaces, Springer-Verlag, New York, 1987.Google Scholar
[L5] Lang, S., Number theory III, Encyclopedia of Mathematical Sciences, vol. 60, Springer Verlag, New York (1991).Google Scholar
[Man] Manin, Y., A course in mathematical logic, Springer-Verlag, New York, 1977.Google Scholar
[Mat] Matijasevic, Y., Enumerable sets are diophantine, Doklady Akademii Nauk SSSR, vol. 191; English translation, Soviet Mathematics Doklady , vol. 11 (1970), pp. 354–358.Google Scholar
[Mo] Morrison, D., Symmetry and rational curves on quintic threefolds: a guide for mathematicians, preprint.Google Scholar
[N] Noguchi, J., A higher dimensional analogue of Mordell's conjecture over function fields, Mathematische Annalen, vol. 258 (1981), pp. 207–212.Google Scholar
[P1] Pheidas, T., Hilbert's tenth problem for fields of rational functions over finite fields, Inventiones Mathematicae, vol. 103 (1991), pp. 1–8.Google Scholar
[P2] Pheidas, T., Extensions of Hilbert's tenth problem, preprint.Google Scholar
[R] Rumely, R., Undecidability and definability for the theory of global fields, Transactions of the American Mathematical Society, vol. 262 (1980), pp. 195–217.Google Scholar
[Sh] Shlapentokh, A., Diophantine definition of integers in rings of rational numbers, Communications on Pure and Applied Mathematics, vol. XCLIV (1991), pp. 853–867.Google Scholar
[S1] Silverman, J., The arithmetic of elliptic curves, Springer-Verlag, New York, 1986.Google Scholar
[S2] Silverman, J., Rational points on K3 surfaces: A new canonical height, Inventiones Mathematicae, vol. 105 (1991), pp. 347–373.Google Scholar
[V1] Vojta, P., Diophantine approximation and value distribution theory, Lecture Notes in Mathematics, vol. 1239, Springer-Verlag, Berlin and New York, 1987.Google Scholar
[V2] Vojta, P., Arithmetic and hyperbolic geometry, preprint.Google Scholar
[V3] Vojta, P., The exceptional set on Büchi surfaces and the n squares problem (to appear).Google Scholar
[Y] Yau, S.-T., Essays on mirror manifolds, International Press, Hong Kong, 1992.Google Scholar