Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Downey, Rod
Hirschfeldt, Denis R.
Nies, André
and
Terwijn, Sebastiaan A.
2006.
Calibrating Randomness.
Bulletin of Symbolic Logic,
Vol. 12,
Issue. 3,
p.
411.
Figueira, Santiago
Stephan, Frank
and
Wu, Guohua
2006.
Randomness and universal machines.
Journal of Complexity,
Vol. 22,
Issue. 6,
p.
738.
Ferbus-Zanda, Marie
and
Grigorieff, Serge
2006.
Kolmogorov complexities Kmax, Kmin on computable partially ordered sets.
Theoretical Computer Science,
Vol. 352,
Issue. 1-3,
p.
159.
Becher, Verónica
and
Grigorieff, Serge
2007.
Random reals à la Chaitin with or without prefix-freeness.
Theoretical Computer Science,
Vol. 385,
Issue. 1-3,
p.
193.
Choffrut, Christian
and
Colson, Loïc
2008.
Preface.
RAIRO - Theoretical Informatics and Applications,
Vol. 42,
Issue. 1,
p.
1.
BECHER, VERÓNICA
and
GRIGORIEFF, SERGE
2015.
Wadge hardness in Scott spaces and its effectivization.
Mathematical Structures in Computer Science,
Vol. 25,
Issue. 7,
p.
1520.
Sureson, Claude
2015.
Random reals as measures of natural open sets.
Theoretical Computer Science,
Vol. 589,
Issue. ,
p.
1.
Sureson, Claude
2016.
Π11-Martin-Löf random reals as measures of natural open sets.
Theoretical Computer Science,
Vol. 653,
Issue. ,
p.
26.
Barmpalias, George
and
Lewis-Pye, Andrew
2017.
Differences of halting probabilities.
Journal of Computer and System Sciences,
Vol. 89,
Issue. ,
p.
349.
Barmpalias, George
Cenzer, Douglas
and
Porter, Christopher P.
2017.
Random numbers as probabilities of machine behavior.
Theoretical Computer Science,
Vol. 673,
Issue. ,
p.
1.
Barmpalias, George
Cenzer, Douglas
and
Porter, Christopher P.
2017.
The Probability of a Computable Output from a Random Oracle.
ACM Transactions on Computational Logic,
Vol. 18,
Issue. 3,
p.
1.
Becher, Verónica
and
Grigorieff, Serge
2022.
Randomness and uniform distribution modulo one.
Information and Computation,
Vol. 285,
Issue. ,
p.
104857.

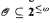 under complexity assumptions about
under complexity assumptions about 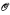 .
.