Published online by Cambridge University Press: 12 March 2014
A Boolean algebra 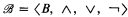 is recursive if B is a recursive subset of the natural numbers N and the operations ∧ (meet), ∨ (join), and ¬ (complement) are partial recursive. Given two Boolean algebras
is recursive if B is a recursive subset of the natural numbers N and the operations ∧ (meet), ∨ (join), and ¬ (complement) are partial recursive. Given two Boolean algebras 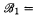
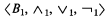 and
and 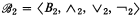 , we write
, we write 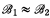 if
if 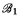 is isomorphic to
is isomorphic to 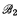 and
and 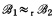 if
if 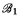 is recursively isomorphic to
is recursively isomorphic to 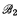 , that is, if there is a partial recursive function f: B1 → B2 which is an isomorphism from
, that is, if there is a partial recursive function f: B1 → B2 which is an isomorphism from 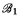 to
to 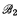 .
. 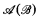 will denote the set of atoms of
will denote the set of atoms of 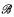 and
and 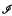 (
(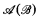 ) will denote the ideal generated by the atoms of
) will denote the ideal generated by the atoms of 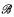 .
.
One of the main questions which motivated this paper is “To what extent does the classical isomorphism type of a recursive Boolean algebra 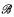 restrict the possible recursion theoretic properties of
restrict the possible recursion theoretic properties of 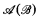 ?” For example, it is easy to see that
?” For example, it is easy to see that 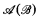 must be co-r.e. (i.e., N −
must be co-r.e. (i.e., N − 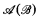 is an r.e. set), but can
is an r.e. set), but can 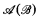 be immune, not immune, cohesive, etc? It follows from a result of Goncharov [4] that there exist classical isomorphism types which contain recursive Boolean algebras but do not contain any recursive Boolean algebras
be immune, not immune, cohesive, etc? It follows from a result of Goncharov [4] that there exist classical isomorphism types which contain recursive Boolean algebras but do not contain any recursive Boolean algebras 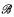 such that
such that 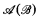 is recursive. Thus the classical isomorphism can restrict the possible Turing degrees of
is recursive. Thus the classical isomorphism can restrict the possible Turing degrees of 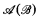 , but what is the extent of this restriction? Another main question is “What is the recursion theoretic relationship between
, but what is the extent of this restriction? Another main question is “What is the recursion theoretic relationship between 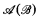 and
and 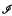 (
(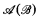 ) in a recursive Boolean algebra?” In our attempt to answer these questions, we were led to a wide variety of recursive isomorphism types which are contained in the classical isomorphism type of any recursive Boolean algebra
) in a recursive Boolean algebra?” In our attempt to answer these questions, we were led to a wide variety of recursive isomorphism types which are contained in the classical isomorphism type of any recursive Boolean algebra  with an infinite set of atoms.
with an infinite set of atoms.