Article contents
A remark on infinitary languages
Published online by Cambridge University Press: 12 March 2014
Extract
In his paper [1] Chang provides among other things answers to questions of the following type: Given two models 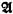 and
and 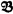 of powers α and β, respectively, what is the least λ such that
of powers α and β, respectively, what is the least λ such that 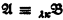 implies
implies 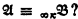 His proofs are by induction on the quantifier rank of formulas and they use an idea which in the case of ordinary first-order language goes back to Ehrenfeucht and Fraïssé. But, as we show, one can easily prove that if λ is big compared with κ and with the cardinality of the universe of the structure
His proofs are by induction on the quantifier rank of formulas and they use an idea which in the case of ordinary first-order language goes back to Ehrenfeucht and Fraïssé. But, as we show, one can easily prove that if λ is big compared with κ and with the cardinality of the universe of the structure 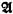 , then every L∞κ-formula is equivalent modulo the set of all Lλκ-sentences which hold in
, then every L∞κ-formula is equivalent modulo the set of all Lλκ-sentences which hold in 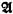 to a Lλκ-formula. From this, Chang's results follow immediately. The same method can be applied to similar problems concerning generalized languages.
to a Lλκ-formula. From this, Chang's results follow immediately. The same method can be applied to similar problems concerning generalized languages.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
References
- 1
- Cited by

