Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Eleftheriou, Pantelis E.
2009.
Compact domination for groups definable in linear o-minimal structures.
Archive for Mathematical Logic,
Vol. 48,
Issue. 7,
p.
607.
Hrushovski, Ehud
Peterzil, Ya'acov
and
Pillay, Anand
2011.
On central extensions and definably compact groups in o-minimal structures.
Journal of Algebra,
Vol. 327,
Issue. 1,
p.
71.
García, Darío
Onshuus, Alf
and
Usvyatsov, Alexander
2012.
Generic stability, forking, and þ-forking.
Transactions of the American Mathematical Society,
Vol. 365,
Issue. 1,
p.
1.
Eleftheriou, Pantelis E.
and
Peterzil, Ya’acov
2012.
Definable quotients of locally definable groups.
Selecta Mathematica,
Vol. 18,
Issue. 4,
p.
885.
Eleftheriou, Pantelis E.
and
Peterzil, Ya’acov
2012.
Definable groups as homomorphic images of semi-linear and field-definable groups.
Selecta Mathematica,
Vol. 18,
Issue. 4,
p.
905.
Eleftheriou, Pantelis E.
2013.
Non-standard lattices and o-minimal groups.
The Bulletin of Symbolic Logic,
Vol. 19,
Issue. 1,
p.
56.
CONVERSANO, ANNALISA
2013.
MAXIMAL COMPACT SUBGROUPS IN THE O-MINIMAL SETTING.
Journal of Mathematical Logic,
Vol. 13,
Issue. 01,
p.
1350004.
Edmundo, Mário J.
Eleftheriou, Pantelis E.
and
Prelli, Luca
2014.
Coverings by open cells.
Archive for Mathematical Logic,
Vol. 53,
Issue. 3-4,
p.
307.
Eleftheriou, Pantelis E.
Peterzil, Ya'acov
and
Ramakrishnan, Janak
2014.
Interpretable groups are definable.
Journal of Mathematical Logic,
Vol. 14,
Issue. 01,
p.
1450002.
Edmundo, Mário J.
Mamino, Marcello
Prelli, Luca
Ramakrishnan, Janak
and
Terzo, Giuseppina
2017.
On Pillay's conjecture in the general case.
Advances in Mathematics,
Vol. 310,
Issue. ,
p.
940.
Eleftheriou, Pantelis E.
and
Savatovsky, Alex
2020.
Expansions of real closed fields that introduce no new smooth functions.
Annals of Pure and Applied Logic,
Vol. 171,
Issue. 7,
p.
102808.
Eleftheriou, Pantelis E.
2021.
Pillay's conjecture for groups definable in weakly o‐minimal non‐valuational structures.
Bulletin of the London Mathematical Society,
Vol. 53,
Issue. 4,
p.
1205.
Eleftheriou, Pantelis E.
2021.
CHARACTERIZING O-MINIMAL GROUPS IN TAME EXPANSIONS OF O-MINIMAL STRUCTURES.
Journal of the Institute of Mathematics of Jussieu,
Vol. 20,
Issue. 2,
p.
699.
Abu Saleh, Hind
and
Peterzil, Ya’acov
2023.
Additive reducts of real closed fields and strongly bounded structures.
Model Theory,
Vol. 2,
Issue. 2,
p.
381.
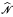 , with the same universe but of different language from N, with (i) Every definable set in N is definable in
, with the same universe but of different language from N, with (i) Every definable set in N is definable in 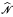 , and (ii)
, and (ii) 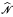 has an elementary substructure in which every bounded interval admits a definable real closed field.
has an elementary substructure in which every bounded interval admits a definable real closed field.
