Hostname: page-component-cb9f654ff-fg9bn Total loading time: 0 Render date: 2025-08-10T05:21:03.223Z Has data issue: false hasContentIssue false
  • English
  • Français

SCOTT COMPLEXITY OF COUNTABLE STRUCTURES

Part of: Computability and recursion theory Model theory

Published online by Cambridge University Press:  01 February 2021

RACHAEL ALVIR ,
NOAM GREENBERG ,
MATTHEW HARRISON-TRAINOR  and
DAN TURETSKY
RACHAEL ALVIR
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF NOTRE DAME SOUTH BEND, IN, USA E-mail: Rachael.C.Alvir.1@nd.edu
NOAM GREENBERG
Affiliation:
SCHOOL OF MATHEMATICS AND STATISTICS VICTORIA UNIVERSITY OF WELLINGTON WELLINGTON, NEW ZEALAND E-mail: greenberg@msor.vuw.ac.nz E-mail: dan.turetsky@vuw.ac.nz
DAN TURETSKY
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF MICHIGAN ANN ARBOR, MI, USA E-mail: matthhar@umich.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We define the Scott complexity of a countable structure to be the least complexity of a Scott sentence for that structure. This is a finer notion of complexity than Scott rank: it distinguishes between whether the simplest Scott sentence is 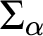$\Sigma _{\alpha }$, 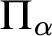$\Pi _{\alpha }$, or 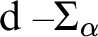$\mathrm {d-}\Sigma _{\alpha }$. We give a complete classification of the possible Scott complexities, including an example of a structure whose simplest Scott sentence is 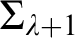$\Sigma _{\lambda + 1}$ for 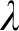$\lambda $ a limit ordinal. This answers a question left open by A. Miller.

We also construct examples of computable structures of high Scott rank with Scott complexities 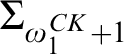$\Sigma _{\omega _1^{CK}+1}$ and 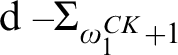$\mathrm {d-}\Sigma _{\omega _1^{CK}+1}$. There are three other possible Scott complexities for a computable structure of high Scott rank: 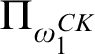$\Pi _{\omega _1^{CK}}$, 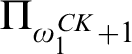$\Pi _{\omega _1^{CK}+1}$, 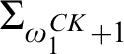$\Sigma _{\omega _1^{CK}+1}$. Examples of these were already known. Our examples are computable structures of Scott rank 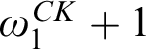$\omega _1^{CK}+1$ which, after naming finitely many constants, have Scott rank 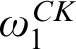$\omega _1^{CK}$. The existence of such structures was an open question.

Keywords

infinitary logicScott rankScott complexity

MSC classification

Primary: 03D45: Theory of numerations, effectively presented structures
Secondary: 03C57: Effective and recursion-theoretic model theory 03C70: Logic on admissible sets

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 4 , December 2021 , pp. 1706 - 1720
Check for updates
Copyright
© Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ash, C. J. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, North-Holland, Amsterdam, 2000.Google Scholar
Carson, J., Harizanov, V. S., Knight, J. F., Lange, K., McCoy, C. F. D., Morozov, A. S., Quinn, S., Safranski, C., and Wallbaum, J., Describing free groups. Transactions of the American Mathematical Society, vol. 364 (2012), no. 11, pp. 5715–5728.10.1090/S0002-9947-2012-05456-0CrossRefGoogle Scholar
Calvert, W., Knight, J. F., and Millar, J., Computable trees of Scott rank ${\omega}_1^{CK}\!\!$ , and computable approximation, this Journal, vol. 71 (2006), no. 1, pp. 283–298.Google Scholar
Harrison, J., Recursive pseudo-well-orderings. Transactions of the American mathematical Society, vol. 131 (1968), pp. 526–543.10.1090/S0002-9947-1968-0244049-7CrossRefGoogle Scholar
Ho, M.-C., Describing groups. Proceedings of the American Mathematical Society, vol. 145 (2017), no. 5, pp. 2223–2239.10.1090/proc/13458CrossRefGoogle Scholar
Harrison-Trainor, M. and Ho, M.-C., On optimal Scott sentences of finitely generated algebraic structures. Proceedings of the American Mathematical Society, vol. 146 (2018), no. 10, pp. 4473–4485.10.1090/proc/14063CrossRefGoogle Scholar
Harrison-Trainor, M., Igusa, G., and Knight, J. F., Some new computable structures of high rank. Proceedings of the American Mathematical Society, vol. 146 (2018), no. 7, pp. 3097–3109.10.1090/proc/13967CrossRefGoogle Scholar
Hirschfeldt, D. R. and White, W. M., Realizing levels of the hyperarithmetic hierarchy as degree spectra of relations on computable structures. Notre Dame Journal of Formal Logic, vol. 43 (2003, 2002), no. 1, pp. 51–64.Google Scholar
Knight, J. F. and Millar, J., Computable structures of rank  ${\omega}_1^{CK}$ . Journal of Mathematical Logic, vol. 10 (2010), no. 1-2, pp. 31–43.10.1142/S0219061310000912CrossRefGoogle Scholar
Knight, J. F. and Saraph, V., Scott sentences for certain groups. Archive for Mathematical Logic, vol. 57 (2018), no. 3-4, pp. 453–472.10.1007/s00153-017-0578-zCrossRefGoogle Scholar
Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long formulas. Fundamenta Mathematicae, vol. 57 (1965), pp. 253–272.10.4064/fm-57-3-253-272CrossRefGoogle Scholar
Makkai, M., An example concerning Scott heights, this Journal, vol. 46 (1981), no. 2, pp. 301–318.Google Scholar
Miller, A. W., On the Borel classification of the isomorphism class of a countable model. Notre Dame Journal of Formal Logic, vol. 24 (1983.), no. 1, pp. 22–34.10.1305/ndjfl/1093870217CrossRefGoogle Scholar
Montalbán, A., A robuster Scott rank. Proceedings of the American Mathematical Society, vol. 143 (2015), no. 12, pp. 5427–5436.10.1090/proc/12669CrossRefGoogle Scholar
Montalbán, A., Effectively existentially-atomic structures, Computability Complexity (Day, A., Fellows, M., Greenberg, N., Khoussainov, B., Melnikov, A., and Rosamond, F., editors), Lecture Notes in Computer Science, vol. 10010, Springer, Cham, 2017, pp. 221–237.10.1007/978-3-319-50062-1_16CrossRefGoogle Scholar
Nadel, M., Scott sentences and admissible sets. Annals of Mathematical Logic, vol. 7 (1974), pp. 267–294.10.1016/0003-4843(74)90017-5CrossRefGoogle Scholar
Scott, D., Logic with denumerably long formulas and finite strings of quantifiers, Theory of Models (Addison, J. W., Henkin, L., and Tarski, A., editors), North-Holland, Amsterdam, 1965, pp. 329–341.Google Scholar
Vaught, R., Invariant sets in topology and logic. Fundamenta Mathematicae, vol. 82 (1974/75), pp. 269–294, Collection of articles dedicated to Andrzej Mostowski on his sixtieth birthday, VII.10.4064/fm-82-3-269-294CrossRefGoogle Scholar
Vanden Boom, M., The effective Borel hierarchy. Fundamenta Mathematicae, vol. 195 (2007), no. 3, pp. 269–289.10.4064/fm195-3-4CrossRefGoogle Scholar
Van Wesep, R., Wadge degrees and descriptive set theory, Cabal Seminar 76–77 (Kechris, A. S. and Moschovakis, Y. N., editors), Lecture Notes in Mathematics, vol. 689, Springer, Berlin, 1978, pp. 151–170.10.1007/BFb0069298CrossRefGoogle Scholar
Wadge, W. W., Reducibility and determinateness on the Baire space , Ph.D. thesis, University of California, Berkeley, ProQuest LLC, Ann Arbor, MI, 1983.Google Scholar