Article contents
Semantic analysis of tense logics1
Published online by Cambridge University Press: 12 March 2014
Extract
Although we believe the results reported below to have direct philosophical import, we shall for the most part confine our remarks to the realm of mathematics. The reader is referred to [4] for a philosophically oriented discussion, comprehensible to mathematicians, of tense logic.
The “minimal” tense logic T0 is the system having connectives ∼, →, F (“at some future time”), and P (“at some past time”); the following axioms:
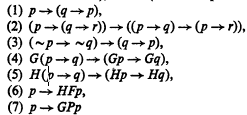
(where G and H abbreviate ∼F∼ and ∼P∼ respectively); and the following rules:
(8) from α and α → β, infer β,
(9) from α, infer any substitution instance of α,
(10) from α, infer Gα,
(11) from α, infer Hα.
A tense logic is a system T whose language is that of T0 and whose axioms and rules include (1)–(11). The axioms and rules of T other than (1)–(11) are called proper axioms and rules.
We shall investigate three systems of semantics for tense logics, i.e. three notions of structure and three relations ⊧ which stand between structures and formulas. One reads 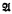 ⊧ α as “α is valid in
⊧ α as “α is valid in 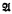 .” A structure
.” A structure 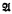 is a model of a tense logic T if every formula provable in T is valid in
is a model of a tense logic T if every formula provable in T is valid in 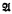 . A semantics is adequate for T if the set of models of T in the semantics is characteristic for T, i.e. if whenever T ∀ α then there is a model
. A semantics is adequate for T if the set of models of T in the semantics is characteristic for T, i.e. if whenever T ∀ α then there is a model 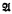 of T in the semantics such that
of T in the semantics such that 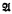 ∀ α. Two structures
∀ α. Two structures 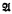 and
and 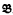 , possibly from different semantics, are called equivalent (
, possibly from different semantics, are called equivalent (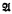 ∼
∼ 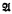 ) if exactly the same formulas are valid in
) if exactly the same formulas are valid in 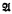 as in
as in 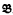 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
Footnotes
This work was supported by the National Research Council of Canada, grant #A-4065, and was contributed to the Tarski Symposium, Berkeley, June, 1971.
References
REFERENCES
- 98
- Cited by

