Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Hamkins, Joel D.
and
Hugh Woodin, W.
2005.
The Necessary Maximality Principle for c. c. c. forcing is equiconsistent with a weakly compact cardinal.
Mathematical Logic Quarterly,
Vol. 51,
Issue. 5,
p.
493.
Friedman, Sy-David
2006.
Internal Consistency and the Inner Model Hypothesis.
Bulletin of Symbolic Logic,
Vol. 12,
Issue. 4,
p.
591.
Hamkins, Joel
and
Löwe, Benedikt
2007.
The modal logic of forcing.
Transactions of the American Mathematical Society,
Vol. 360,
Issue. 4,
p.
1793.
2007.
Handbook of Modal Logic.
Vol. 3,
Issue. ,
p.
927.
Hamkins, Joel David
2008.
Logic and Its Applications.
Vol. 5378,
Issue. ,
p.
36.
Leibman, George
2010.
The Consistency Strength of M P C C C ( R ).
Notre Dame Journal of Formal Logic,
Vol. 51,
Issue. 2,
Coskey, Samuel
and
Hamkins, Joel David
2011.
Infinite Time Decidable Equivalence Relation Theory.
Notre Dame Journal of Formal Logic,
Vol. 52,
Issue. 2,
DAVID HAMKINS, Joel
2011.
The Set-theoretic Multiverse : A Natural Context for Set Theory(<Special Section>Mathematical Logic and Its Applications).
Annals of the Japan Association for Philosophy of Science,
Vol. 19,
Issue. 0,
p.
37.
HAMKINS, JOEL DAVID
2012.
THE SET-THEORETIC MULTIVERSE.
The Review of Symbolic Logic,
Vol. 5,
Issue. 3,
p.
416.
Hamkins, Joel David
and
Löwe, Benedikt
2013.
Logic and Its Applications.
Vol. 7750,
Issue. ,
p.
139.
Hamkins, Joel David
and
Johnstone, Thomas A.
2014.
Resurrection axioms and uplifting cardinals.
Archive for Mathematical Logic,
Vol. 53,
Issue. 3-4,
p.
463.
Hamkins, Joel David
Leibman, George
and
Löwe, Benedikt
2015.
Structural connections between a forcing class and its modal logic.
Israel Journal of Mathematics,
Vol. 207,
Issue. 2,
p.
617.
Henk, Paula
2015.
Logic, Language, and Computation.
Vol. 8984,
Issue. ,
p.
157.
Incurvati, Luca
2016.
Maximality Principles in Set Theory.
Philosophia Mathematica,
p.
nkw011.
Usuba, Toshimichi
2017.
The downward directed grounds hypothesis and very large cardinals.
Journal of Mathematical Logic,
Vol. 17,
Issue. 02,
p.
1750009.
Aspero, David
2017.
Logic Colloquium '02.
p.
1.
Chalki, Aggeliki
Koutras, Costas D
and
Zikos, Yorgos
2018.
A quick guided tour to the modal logic S4.2.
Logic Journal of the IGPL,
Vol. 26,
Issue. 4,
p.
429.
Ikegami, Daisuke
and
Trang, Nam
2018.
On a class of maximality principles.
Archive for Mathematical Logic,
Vol. 57,
Issue. 5-6,
p.
713.
Fuchs, Gunter
2018.
Subcomplete forcing principles and definable well‐orders.
Mathematical Logic Quarterly,
Vol. 64,
Issue. 6,
p.
487.
FRITZ, PETER
LEDERMAN, HARVEY
LIU, TIANKAI
and
SCOTT, DANA
2018.
CAN MODALITIES SAVE NAIVE SET THEORY?.
The Review of Symbolic Logic,
Vol. 11,
Issue. 1,
p.
21.
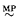 , which asserts that
, which asserts that 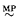 holds in V and all forcing extensions. From this, it follows that 0# exists, that x# exists for every set x, that projective truth is invariant by forcing, that Woodin cardinals are consistent and much more. Many open questions remain.
holds in V and all forcing extensions. From this, it follows that 0# exists, that x# exists for every set x, that projective truth is invariant by forcing, that Woodin cardinals are consistent and much more. Many open questions remain.
