By a “partly numerical structure” (p.n.s.) we shall here mean a quadruple 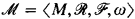, where M is a set, ω = the natural numbers, ω ⊆ M, 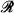and 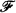are disjoint sets, 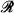is a set of relations (of various positive integral arities) on M, and 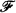is a set of functions (of various positive integral arities) with arguments and values in M. Thus, in calculated disharmony with common practice, we do not (except as noted below, in connection with naming the elements of ω) fix a similarity type as part of our notion of a “structure”. Suppose a finitary first-order language 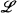(with identity) has been specified, with constant symbols 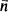, n ∈ ω, and with exactly enough relation and function symbols of each arity to enable us to interpret 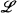in 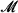. We wish to consider the variation in the degree (relative to a fixed Gödel-numbering of 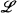) of the complete 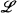-theory of 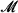as we vary the way in which elements of 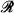∪ 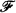are assigned as interpretations to the relation and function symbols of 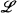. We shall in fact, therefore, be concerned exclusively with p.n.s.'s 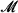for which 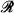∪ 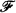is countable. More: we assume 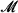to be such that we can effectively tell, uniformly in n > 0, exactly how many n-ary relations 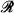has and exactly how many n-ary function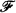s has.