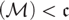Hostname: page-component-76c49bb84f-ndtt8 Total loading time: 0 Render date: 2025-07-03T00:34:34.059Z Has data issue: false hasContentIssue false
  • English
  • Français

STABLE ORDERED UNION ULTRAFILTERS AND cov $\left( \mathcal{M} \right) < \mathfrak{c}$

Published online by Cambridge University Press:  03 April 2019

DAVID JOSÉ FERNÁNDEZ-BRETÓN
DAVID JOSÉ FERNÁNDEZ-BRETÓN*
Affiliation:
DEPARTMENT OF MATHEMATICS, UNIVERSITY OF MICHIGAN 2074 EAST HALL, 530 CHURCH STREET ANN ARBOR, MICHIGAN, 48109, USA and KURT GÖDEL RESEARCH CENTER FOR MATHEMATICAL LOGIC UNIVERSITY OF VIENNA WÄRINGER STRAßE 25, 1090WIEN, AUSTRIAE-mail: david.fernandez-breton@univie.ac.atURL: https://homepage.univie.ac.at/david.fernandez-breton/
Get access Rights & Permissions [Opens in a new window]

Abstract

A union ultrafilter is an ultrafilter over the finite subsets of ω that has a base of sets of the form 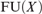${\text{FU}}\left( X \right)$, where X is an infinite pairwise disjoint family and 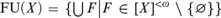${\text{FU}}(X) = \left\{ {\bigcup {F|F} \in [X]^{ < \omega } \setminus \{ \emptyset \} } \right\}$. The existence of these ultrafilters is not provable from the 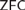$ZFC$ axioms, but is known to follow from the assumption that 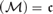${\text{cov}}\left( \mathcal{M} \right) = \mathfrak{c}$. In this article we obtain various models of 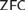$ZFC$ that satisfy the existence of union ultrafilters while at the same time 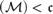${\text{cov}}\left( \mathcal{M} \right) = \mathfrak{c}$.

Keywords

Primary 03E35Secondary 03E1754D8022A15ultrafiltersHindman’s theoremiterated forcingproper forcingcardinal characteristics of the continuum

Information

Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 3 , September 2019 , pp. 1176 - 1193
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Balcar, B., Doucha, M., and Hrušák, M., Base tree property.Order, vol. 32 (2015), pp. 69–81.Google Scholar
Bartoszyński, T. and Judah, H., Set Theory. On the Structure of the Real Line, Peters, A. K., Wellesley, Massachusetts, 1995.Google Scholar
Baumgartner, J., A short proof of Hindman’s theorem. Journal of Combinatorial Theory, Series A, vol. 17 (1974), pp. 384–386.Google Scholar
Blass, A., Ultrafilters related to Hindman’s finite-unions theorem and its extensions, Logic and Combinatorics (Simpson, S., editor), Contemporary Mathematics, vol. 65, American Mathematical Society, Providence, RI, 1987, pp. 89–124.Google Scholar
Blass, A., Combinatorial cardinal characteristics of the continuum, Handbook of Set Theory, vol. 1 (Foreman, M. and Kanamori, A., editors), Springer, Amsterdam, 2010, pp. 395–489.Google Scholar
Blass, A. and Hindman, N., On strongly summable ultrafilters and union ultrafilters. Transactions of the American Mathematical Society, vol. 304 (1987), no. 1, pp. 83–99.Google Scholar
Blass, A. and Shelah, S., Ultrafilters with small generating sets. Israel Journal of Mathematics, vol. 65 (1989), no. 3, pp. 259–271.Google Scholar
Eisworth, T., Forcing and stable-ordered union ultrafilters, this Journal, vol. 67 (2002), no. 1, pp. 449–464.Google Scholar
Ellis, R., Distal transformation groups. Pacific Journal of Mathematics, vol. 8 (1958), no. 3, pp. 401–405.Google Scholar
Bretón, D. F., Strongly summable ultrafilters: Some properties and generalizations, Ph.D. thesis, York University, 2015.Google Scholar
Fernández-Bretón, D. and Hrušák, M., A parametrized diamond principle and union ultrafilters.Colloquium Mathematicum, vol. 153 (2018), pp. 261–271.Google Scholar
García-Ávila, L. M., Forcing arguments in infinite Ramsey theory, Ph.D. thesis, Universitat de Barcelona, 2013.Google Scholar
García-Ávila, L. M., A forcing notion related to Hindman’s theorem. Archive for Mathematical Logic, vol. 54 (2015), pp. 133–159.Google Scholar
Goldstern, M., Kellner, J., Shelah, S., and Wohofsky, W., Borel conjecture and dual Borel conjecture. Transactions of the American Mathematical Society, vol. 366 (2014), pp. 245–307.Google Scholar
Hindman, N., The existence of certain ultrafilters on $\mathbb{N}$ and a conjecture of Graham and Rothschild. Proceedings of the American Mathematical Society, vol. 36 (1972), no. 2, pp. 341–346.Google Scholar
Hindman, N., Finite sums from sequences within cells of a partition of N. Journal of Combinatorial Theory, Series A, vol. 17 (1974), pp. 1–11.Google Scholar
Hindman, N. and Strauss, D., Algebra in the Stone-Čech Compactification , second ed., Walter de Gruyter, Berlin, 2012.Google Scholar
Jech, T., Set Theory, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
Matet, P., Partitions and filters, this Journal, vol. 51 (1986), no. 1, pp. 12–21.Google Scholar
Matet, P., Some filters of partitions, this Journal, vol. 53 (1988), no. 2, pp. 540–553.Google Scholar
Mildenberger, H., Local Ramsey Spaces in Matet Forcing Extensions and Finitely Many Near-Coherence Classes, arXiv preprint, 2018, arXiv:1404.7350.Google Scholar
Numakura, K., On bicompact semigroups. Mathematical Journal of Okayama University, vol. 1 (1952), pp. 99–108.Google Scholar
Roitman, J., p-points in iterated forcing extensions. Proceedings of the American Mathematical Society, vol. 69 (1978), no. 2, pp. 314–318.Google Scholar
Shelah, S., Proper and Improper Forcing, Perspectives in Mathematical Logic, Springer, Berlin, 1998.Google Scholar
Shelah, S. and Spinas, O., The distributivity numbers of $\mathcal{P}\left( \omega \right)/{\text{FIN}}$ and its square. Transactions of the American Mathematical Society , vol. 352 (2000), no. 5, pp. 2023–2047.Google Scholar