Article contents
STRONG REDUCTIONS BETWEEN COMBINATORIAL PRINCIPLES
Published online by Cambridge University Press: 01 December 2016
Abstract
This paper is a contribution to the growing investigation of strong reducibilities between 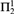 ${\rm{\Pi }}_2^1$ statements of second-order arithmetic, viewed as an extension of the traditional analysis of reverse mathematics. We answer several questions of Hirschfeldt and Jockusch [13] about Weihrauch (uniform) and strong computable reductions between various combinatorial principles related to Ramsey’s theorem for pairs. Among other results, we establish that the principle
${\rm{\Pi }}_2^1$ statements of second-order arithmetic, viewed as an extension of the traditional analysis of reverse mathematics. We answer several questions of Hirschfeldt and Jockusch [13] about Weihrauch (uniform) and strong computable reductions between various combinatorial principles related to Ramsey’s theorem for pairs. Among other results, we establish that the principle 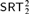 $SRT_2^2$ is not Weihrauch or strongly computably reducible to
$SRT_2^2$ is not Weihrauch or strongly computably reducible to 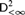 $D_{ < \infty }^2$ , and that COH is not Weihrauch reducible to
$D_{ < \infty }^2$ , and that COH is not Weihrauch reducible to 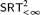 $SRT_{ < \infty }^2$ , or strongly computably reducible to
$SRT_{ < \infty }^2$ , or strongly computably reducible to 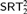 $SRT_2^2$ . The last result also extends a prior result of Dzhafarov [9]. We introduce a number of new techniques for controlling the combinatorial and computability-theoretic properties of the problems and solutions we construct in our arguments.
$SRT_2^2$ . The last result also extends a prior result of Dzhafarov [9]. We introduce a number of new techniques for controlling the combinatorial and computability-theoretic properties of the problems and solutions we construct in our arguments.
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2016
References
REFERENCES
- 13
- Cited by

