Hostname: page-component-76fb5796d-vfjqv Total loading time: 0 Render date: 2024-04-29T12:41:37.224Z Has data issue: false hasContentIssue false
  • English
  • Français

Theories of presheaf type

Published online by Cambridge University Press:  12 March 2014

Tibor Beke
Tibor Beke*
Affiliation:
Department of Mathematics, University of Michigan, East Hall, 525 East University Avenue, Ann Arbor, MI 48109-1109, USA, E-mail: beke@umich.edu
Get access Rights & Permissions [Opens in a new window]

Extract

Let us say that a geometric theory T is of presheaf type if its classifying topos 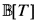is (equivalent to) a presheaf topos. (We adhere to the convention that geometric logic allows arbitrary disjunctions, while coherent logic means geometric and finitary.) Write Mod(T) for the category of Set-models and homomorphisms of T. The next proposition is well known; see, for example, MacLane–Moerdijk [13], pp. 381-386, and the textbook of Adámek–Rosický [1] for additional information:

Proposition 0.1. For a category 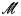, the following properties are equivalent:

(i) 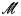is a finitely accessible category in the sense of Makkai–Paré [14], i.e., it has filtered colimits and a small dense subcategory 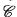of finitely presentable objects

ii) 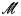is equivalent to Pts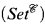, the category of points of some presheaf topos

(iii) 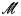is equivalent to the free filtered cocompletion (also known as Ind-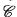) of a small category .

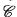(iv) 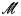is equivalent to Mod(T) for some geometric theory of presheaf type.

Moreover, if these are satisfied for a given 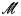, then the 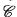—in any of (i), (ii) and (iii)—can be taken to be the full subcategory of 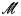consisting of finitely presentable objects. (There may be inequivalent choices of 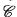, as it is in general only determined up to idempotent completion; this will not concern us.)

This seems to completely solve the problem of identifying when T is of presheaf type: check whether Mod(T) is finitely accessible and if so, recover the presheaf topos as Set-functors on the full subcategory of finitely presentable models. There is a subtlety here, however, as pointed out (probably for the first time) by Johnstone [10].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 69 , Issue 3 , September 2004 , pp. 923 - 934
Copyright
Copyright © Association for Symbolic Logic 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Adámek, Jiří and Rosický, Jiří, Locally presentable and accessible categories, London Mathematical Society Lecture Note Series, no. 189. Cambridge University Press, 1994.CrossRefGoogle Scholar
[2]Baumslag, G., Dyer, E., and Heller, A., The topology of discrete groups, Journal of Pure and Applied Algebra, vol. 16 (1980), no. 1, pp. 1–47.CrossRefGoogle Scholar
[3]Bousfield, A. K. and Kan, D. M., Homotopy limits, completions and localizations, Lecture Notes in Mathematics, vol. 304, Springer-Veriag, 1972.CrossRefGoogle Scholar
[4]Coste, Michel, Localisation, spectra and sheaf representation, Applications of sheaves, Lecture Notes in Mathematics, vol. 753, Springer-Veriag, 1979, pp. 212–238.CrossRefGoogle Scholar
[5]Gabriel, Pierre and Zisman, Michel, Calculus of fractions and homotopy theory, Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 35, Springer-Veriag, 1967.CrossRefGoogle Scholar
[6]Goerss, Paul G. and Jardine, John F., Simplicial homotopy theory, Progress in Mathematics, vol. 174, Birkhäuser Veriag, 1999.CrossRefGoogle Scholar
[7]Hodges, Wilfrid, Models built on linear orderings, Orders: description and roles, North-Holland Mathematics Studies, vol. 99, North-Holland, 1984, pp. 207–234.Google Scholar
[8]Jensen, C. U., Some cardinality questions for flat modules and coherence, Journal of Algebra, vol. 12 (1969), pp. 231–241.CrossRefGoogle Scholar
[9]Johnstone, P. T., Topos theory, London Mathematical Society Monographs, vol. 10, Academic Press, 1977.Google Scholar
[10]Johnstone, P. T., A syntactic approach to Diers’ localizable categories, Applications of sheaves, Lecture Notes in Mathematics, vol. 753, Springer-Verlag, 1979, pp. 466–478.CrossRefGoogle Scholar
[11]Johnstone, P. T., Stone spaces, Cambridge University Press, 1982.Google Scholar
[12]Joyal, André and Wraith, Gavin, Eilenberg-MacLane toposes and cohomology, Mathematical applications of category theory, Contemporary Mathematics, vol. 30, American Mathematical Society, 1984, pp. 117–131.CrossRefGoogle Scholar
[13]MacLane, Saunders and Moerdijk, Ieke, Sheaves in geometry and logic, Springer-Veriag, 1992.Google Scholar
[14]Makkai, Michael and Paré, Robert, Accessible categories: the foundations of categorical model theory, Contemporary Mathematics, vol. 104, American Mathematical Society, 1989.CrossRefGoogle Scholar
[15]Makkai, Michael and Reyes, Gonzalo E., First order categorical logic. Model-theoretical methods in the theory of topoi and related categories, Lecture Notes in Mathematics, vol. 611, Springer-Veriag, 1977.CrossRefGoogle Scholar
[16]Moerdijk, Ieke, Cyclic sets as a classifying topos, Unpublished manuscript, Utrecht, 1995.Google Scholar
[17]Tierney, Myles, Forcing topologies and classifying topoi, Algebra, topology, and category theory, Academic Press, 1976.CrossRefGoogle Scholar
[18]Wraith, Gavin C., Toposes and simplicial sets: the cohomological connection. A report on joint work with A. Joyal, Category theoretic methods in geometry, Various Publications Series, no. 35, Aarhus University, 1983, pp. 281–290.Google Scholar