Hostname: page-component-784d4fb959-wvrvt Total loading time: 0 Render date: 2025-07-15T14:46:03.056Z Has data issue: false hasContentIssue false
  • English
  • Français

Ultrafilters on the natural numbers

Published online by Cambridge University Press:  12 March 2014

Christopher Barney
Christopher Barney*
Affiliation:
Department of Mathematics, University of California, Irvine, Irvine, California 92612, USA, E-mail: silvain@alum.mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the problem of existence and generic existence of ultrafilters on ω. We prove a conjecture of Jörg Brendle's showing that there is an ultrafilter that is countably closed but is not an ordinal ultrafilter under CH. We also show that Canjar's previous partial characterization of the generic existence of Q-points is the best that can be done. More simply put, there is no normal cardinal invariant equality that fully characterizes the generic existence of Q-points. We then sharpen results on generic existence with the introduction of σ-compact ultrafilters. We show that the generic existence of said ultrafilters is equivalent to 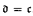. This result, taken along with our result that there exists a Kσ, non-countably closed ultrafilter under CH, expands the size of the class of ultrafilters that were known to fit this description before. From the core of the proof, we get a new result on the cardinal invariants of the continuum, i.e., the cofinality of the sets with σ-compact closure is .

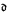Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 68 , Issue 3 , September 2003 , pp. 764 - 784
Copyright
Copyright © Association for Symbolic Logic 2003

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1] Bartoszyński, T. and Judah, H., Set theory, on the structure of the real line, A K Peters Ltd., Wellesley, Massachusetts, 1995.Google Scholar
[2] Baumgartner, J., Ultrafilters on ω , this Journal, vol. 60 (1995), pp. 624–639.Google Scholar
[3] Baumgartner, J. and Dordal, P., Adjoining dominating functions, this Journal, vol. 50 (1985), pp. 94–101.Google Scholar
[4] Brendle, J., Between P-points and nowhere dense ultrafilters, Israel Journal of Mathematics, vol. 113 (1999), pp. 205–230.Google Scholar
[5] Canjar, R. M., On the generic existence of special ultrafilters, Proceedings of the American Mathematical Society, vol. 110 (1990), pp. 233–241.CrossRefGoogle Scholar
[6] Jech, T., Set theory, Academic Press, New York, 1978.Google Scholar
[7] Ketonen, J., On the existence of P-points in the Stone-Čech compactification of integers, Fundamenta Mathematicae, vol. 92 (1976), pp. 91–94.Google Scholar
[8] Shelah, S., Vive la différence. I. Nonisomorphism of ultrapowers of countable models, Set theory of the continuum (Judah, H., Just, W., and Woodin, H., editors), MSRI series, vol. 26, Springer-Verlag, New York, 1992, pp. 357–405.Google Scholar
[9] Shelah, S., There may be no nowhere dense ultrafilter, Proceedings of the logic colloquium Haifa '95, Lecture Notes Logic, vol. 11, Springer, Berlin, 1998, pp. 305–324.Google Scholar
[10] Shelah, S., On what I do not understand (and have something to say). Fundamenta Mathematicae, vol. 166 (2000), pp. 1–82.CrossRefGoogle Scholar