Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-24T04:39:23.863Z Has data issue: false hasContentIssue false
  • English
  • Français

Ultraproducts which are not saturated

Published online by Cambridge University Press:  12 March 2014

H. Jerome Keisler
H. Jerome Keisler*
Affiliation:
University of Wisconsin
Get access Rights & Permissions [Opens in a new window]

Extract

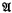In this paper we continue our study, begun in [5], of the connection between ultraproducts and saturated structures. If D is an ultrafilter over a set I, and is a structure (i.e., a model for a first order predicate logic ℒ), the ultrapower of 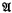modulo D is denoted by D-prod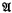. The ultrapower is important because it is a method of constructing structures which are elementarily equivalent to a given structure 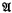(see Frayne-Morel-Scott [3]). Our ultimate aim is to find out what kinds of structure are ultrapowers of 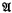. We made a beginning in [5] by proving that, assuming the generalized continuum hypothesis (GCH), for each cardinal α there is an ultrafilter D over a set of power α such that for all structures 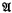, D-prod 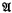is α+-saturated.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 32 , Issue 1 , June 1967 , pp. 23 - 46
Copyright
Copyright © Association for Symbolic Logic 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Chang, C. C. and Keisler, H. J., Continuous model theory, Princeton Univ. Press, Princeton, N.J., 1966, xii+ 165 pp.CrossRefGoogle Scholar
[2]Ehrenfeucht, A., On theories categorical in power, Fundamenta Mathematicae, vol. 44 (1957), pp. 241–248.CrossRefGoogle Scholar
[3]Frayne, T., Morel, A. and Scott, D., Reduced direct products, Fundamenta Mathematicae, vol. 51 (1962), pp. 195–248.CrossRefGoogle Scholar
[4]Keisler, H. J., Ultraproducts and elementary classes, Indagationes Mathematicae, vol. 23 (1962), pp. 447–495; Koninklijke Nederlandse Akademie van Wetenschappen. Proceedings. Series A, 64.Google Scholar
[5]Keisler, H. J., Ultraproducts and saturated models, Indagationes Mathematical, vol. 26 (1964) pp. 178–186.CrossRefGoogle Scholar
[6]Keisler, H. J., Replete relational systems, Notices of the American Mathematical Society, vol. 8 (1961), p. 63.Google Scholar
[7]Kebler, H. J., Good ideals in fields of sets, Annals of Mathematics, vol. 79 (1964), pp. 338–359.Google Scholar
[8]Keisler, H. J., Ideals with prescribed degree of goodness, Annals of Mathematics, vol. 81 (1965), pp. 112–116.Google Scholar
[9]Keisler, H. J., On cardinalities of ultraproducts, Bulletin of the American Mathematical Society, vol. 70 (1964), pp. 644–647.CrossRefGoogle Scholar
[10]Keisler, H. J., A survey of ultraproducts, Logic, methodology, and the philosophy of science, Proceedings of the 1964 International Congress, pp. 112–126, Jerusalem, 1965.Google Scholar
[11]Łos, J., On the categoricity in power of elementary deductive systems, Colloquium Mathematicum, vol. 3 (1954), pp. 58–62.CrossRefGoogle Scholar
[12]Łos, J., Quelques remarques, théorèmes et problèmes sur les classes définissables d'algèbres, Mathematical Interpretations of formal systems, North-Holland, Amsterdam, 1955, pp. 98–113.CrossRefGoogle Scholar
[13]Morley, M., Categoricity in power, Doctoral dissertation, University of Chicago, Chicago, Ill., 1962; Transactions of the American Mathematical Society, vol. 114 (1965), pp. 514–518.Google Scholar
[14]Morley, M. and Vaught, R., Homogeneous universal models, Mathematica Scandinavica, vol. 11 (1962), pp. 37–57.CrossRefGoogle Scholar
[15]Ramsey, F. P., On a problem of formal logic, Proceedings of the London Mathematical Society, Series 2, vol. 30 (1929), pp. 291–310.Google Scholar
[16]Tarski, A., Une contribution à la théorie de la mesure, Fundamenta Mathematicae, vol. 15 (1930), pp. 42–50.CrossRefGoogle Scholar
[17]Tarski, A., Some notions and methods on the borderline of algebra and metamathematics, Proceedings of the International Congress of Mathematicians, 1950, 705–720; Cambridge, 1950.Google Scholar
[18]Tarski, A., Contributions to the theory of models. I, II, Indagationes Mathematicae, vol. 16 (1954), 572–588; Koninklijke Nederlandse Akademie van Wetenschappen. Proceedings. Series A, 57.CrossRefGoogle Scholar
[19]Tarski, A., Mostowski, A. and Robinson, R., Undecidable theories, Amsterdam, 1953.Google Scholar
[20]Tarski, A. and Vaught, R., Arithmetical extensions of relational systems, Compositio Mathematica, vol. 13 (1957), pp. 81–102.Google Scholar
[21]Vaught, R., Models of complete theories, Bulletin of the American Mathematical Society, vol. 69 (1963), pp. 299–313.CrossRefGoogle Scholar
[22]Vaught, R., Applications of the Löwenheim-Skolem-Tarski theorem to problems of completeness and decidability, Indagationes Mathematicae, vol. 16 (1954), 467–472; Koninklijke Nederlandse Akademie van Wetenschappen. Proceedings. Series A, 57.CrossRefGoogle Scholar