Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gavruskin, Alexander
Jain, Sanjay
Khoussainov, Bakhadyr
and
Stephan, Frank
2014.
Graphs realised by r.e. equivalence relations.
Annals of Pure and Applied Logic,
Vol. 165,
Issue. 7-8,
p.
1263.
Downey, Rod
Melnikov, Alexander G.
and
Ng, Keng Meng
2015.
OnΔ20-categoricity of equivalence relations.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 9,
p.
851.
Badaev, Serikzhan
and
Sorbi, Andrea
2016.
Weakly precomplete computably enumerable equivalence relations.
Mathematical Logic Quarterly,
Vol. 62,
Issue. 1-2,
p.
111.
Downey, Rodney G.
Melnikov, Alexander G.
and
Ng, Keng Meng
2017.
A Friedberg enumeration of equivalence structures.
Journal of Mathematical Logic,
Vol. 17,
Issue. 02,
p.
1750008.
Andrews, Uri
Badaev, Serikzhan
and
Sorbi, Andrea
2017.
Computability and Complexity.
Vol. 10010,
Issue. ,
p.
418.
Andrews, Uri
and
Sorbi, Andrea
2018.
Jumps of computably enumerable equivalence relations.
Annals of Pure and Applied Logic,
Vol. 169,
Issue. 3,
p.
243.
NIES, ANDRÉ
and
SORBI, ANDREA
2018.
Calibrating word problems of groups via the complexity of equivalence relations.
Mathematical Structures in Computer Science,
Vol. 28,
Issue. 3,
p.
457.
Khoussainov, Bakh
2018.
Sailing Routes in the World of Computation.
Vol. 10936,
Issue. ,
p.
1.
Kabylzhanova, D. K.
2018.
Positive Preorders.
Algebra and Logic,
Vol. 57,
Issue. 3,
p.
182.
Bazhenov, N. A.
and
Kalmurzaev, B. S.
2018.
On Dark Computably Enumerable Equivalence Relations.
Siberian Mathematical Journal,
Vol. 59,
Issue. 1,
p.
22.
Bazhenov, Nikolay
Mustafa, Manat
and
Yamaleev, Mars
2019.
Elementary theories and hereditary undecidability for semilattices of numberings.
Archive for Mathematical Logic,
Vol. 58,
Issue. 3-4,
p.
485.
Fokina, Ekaterina
Rossegger, Dino
San Mauro, Luca
Brattka, Vasco
Downey, Rod
Knight, Julia F.
and
Lempp, Steffen
2019.
Measuring the complexity of reductions between equivalence relations.
Computability,
Vol. 8,
Issue. 3-4,
p.
265.
Bazhenov, Nikolay
Mustafa, Manat
and
Yamaleev, Mars
2019.
Theory and Applications of Models of Computation.
Vol. 11436,
Issue. ,
p.
28.
Ng, Keng Meng
and
Yu, Hongyuan
2019.
On the Degree Structure of Equivalence Relations Under Computable Reducibility.
Notre Dame Journal of Formal Logic,
Vol. 60,
Issue. 4,
Andrews, Uri
Sorbi, Andea
Brattka, Vasco
Downey, Rod
Knight, Julia F.
and
Lempp, Steffen
2019.
Joins and meets in the structure of ceers.
Computability,
Vol. 8,
Issue. 3-4,
p.
193.
Andrews, Uri
Schweber, Noah
and
Sorbi, Andrea
2020.
Self-full ceers and the uniform join operator.
Journal of Logic and Computation,
Vol. 30,
Issue. 3,
p.
765.
Badaev, S. A.
Bazhenov, N. A.
and
Kalmurzaev, B. S.
2020.
The Structure of Computably Enumerable Preorder Relations.
Algebra and Logic,
Vol. 59,
Issue. 3,
p.
201.
Bazhenov, Nikolay
Mustafa, Manat
San Mauro, Luca
Sorbi, Andrea
and
Yamaleev, Mars
2020.
Classifying equivalence relations in the Ershov hierarchy.
Archive for Mathematical Logic,
Vol. 59,
Issue. 7-8,
p.
835.
Delle Rose, Valentino
San Mauro, Luca
and
Sorbi, Andrea
2020.
Word problems and ceers.
Mathematical Logic Quarterly,
Vol. 66,
Issue. 3,
p.
341.
Epstein, Rachel
and
Lange, Karen
2020.
Agreement reducibility.
Mathematical Logic Quarterly,
Vol. 66,
Issue. 4,
p.
448.
 $R \le S$ if there exists a computable function f suchthat
$R \le S$ if there exists a computable function f suchthat 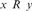 $x\,R\,y$ if and only if
$x\,R\,y$ if and only if 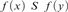 $f\left( x \right)\,\,S\,f\left( y \right)$, for every
$f\left( x \right)\,\,S\,f\left( y \right)$, for every 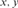 $x,y$. We show that the degrees of ceers under the equivalencerelation generated by
$x,y$. We show that the degrees of ceers under the equivalencerelation generated by 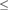 $\le$ form a bounded poset that is neither a lower semilattice, noran upper semilattice, and its first-order theory is undecidable. We then studythe universal ceers. We show that 1) the uniformly effectively inseparable ceersare universal, but there are effectively inseparable ceers that are notuniversal; 2) a ceer R is universal if and only if
$\le$ form a bounded poset that is neither a lower semilattice, noran upper semilattice, and its first-order theory is undecidable. We then studythe universal ceers. We show that 1) the uniformly effectively inseparable ceersare universal, but there are effectively inseparable ceers that are notuniversal; 2) a ceer R is universal if and only if 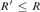 $R\prime \le R$, where
$R\prime \le R$, where 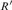 $R\prime$ denotes the halting jump operator introduced by Gao and Gerdes(answering an open question of Gao and Gerdes); and 3) both the index set of theuniversal ceers and the index set of the uniformly effectively inseparable ceersare
$R\prime$ denotes the halting jump operator introduced by Gao and Gerdes(answering an open question of Gao and Gerdes); and 3) both the index set of theuniversal ceers and the index set of the uniformly effectively inseparable ceersare 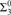 ${\rm{\Sigma }}_3^0$-complete (the former answering an open question of Gao andGerdes).
${\rm{\Sigma }}_3^0$-complete (the former answering an open question of Gao andGerdes).
