Article contents
UNIVERSAL ROSSER PREDICATES
Published online by Cambridge University Press: 21 March 2017
Abstract
Gödel introduced the original provability predicate in the proofs of Gödel’s incompleteness theorems, and Rosser defined a new one. They are equivalent in the standard model  ${\mathbb N}$ of arithmetic or any nonstandard model of
${\mathbb N}$ of arithmetic or any nonstandard model of 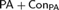 ${\rm PA} + {\rm Con_{PA}} $ , but the behavior of Rosser’s provability predicate is different from the original one in nonstandard models of
${\rm PA} + {\rm Con_{PA}} $ , but the behavior of Rosser’s provability predicate is different from the original one in nonstandard models of 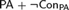 ${\rm PA} + \neg {\rm Con_{PA}} $ . In this paper, we investigate several properties of the derivability conditions for Rosser provability predicates, and prove the existence of a Rosser provability predicate with which we can define any consistent complete extension of
${\rm PA} + \neg {\rm Con_{PA}} $ . In this paper, we investigate several properties of the derivability conditions for Rosser provability predicates, and prove the existence of a Rosser provability predicate with which we can define any consistent complete extension of 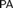 ${\rm PA}$ in some nonstandard model of
${\rm PA}$ in some nonstandard model of 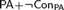 ${\rm PA} + \neg {\rm Con_{PA}} $ . We call it a universal Rosser predicate. It follows from the theorem that the true arithmetic
${\rm PA} + \neg {\rm Con_{PA}} $ . We call it a universal Rosser predicate. It follows from the theorem that the true arithmetic 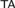 ${\rm TA}$ can be defined as the set of theorems of
${\rm TA}$ can be defined as the set of theorems of 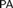 ${\rm PA}$ in terms of a universal Rosser predicate in some nonstandard model of
${\rm PA}$ in terms of a universal Rosser predicate in some nonstandard model of 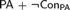 ${\rm PA} + \neg {\rm Con_{PA}} $ . By using this theorem, we also give a new proof of a theorem that there is a nonstandard model M of
${\rm PA} + \neg {\rm Con_{PA}} $ . By using this theorem, we also give a new proof of a theorem that there is a nonstandard model M of 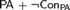 ${\rm PA} + \neg {\rm Con_{PA}} $ such that if N is an initial segment of M which is a model of
${\rm PA} + \neg {\rm Con_{PA}} $ such that if N is an initial segment of M which is a model of 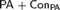 ${\rm PA} + {\rm Con_{PA}} $ then every theorem of
${\rm PA} + {\rm Con_{PA}} $ then every theorem of 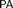 ${\rm PA}$ in N is a theorem of
${\rm PA}$ in N is a theorem of 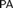 $\rm PA$ in
$\rm PA$ in  ${\mathbb N}$ . In addition, we prove that there is a Rosser provability predicate such that the set of theorems of
${\mathbb N}$ . In addition, we prove that there is a Rosser provability predicate such that the set of theorems of 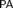 $\rm PA$ in terms of the Rosser provability predicate is inconsistent in any nonstandard model of
$\rm PA$ in terms of the Rosser provability predicate is inconsistent in any nonstandard model of 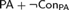 ${\rm PA} + \neg {\rm Con_{PA}} $ .
${\rm PA} + \neg {\rm Con_{PA}} $ .
Keywords
Information
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2017
References
REFERENCES
- 5
- Cited by

