The comprehension principle of second order arithmetic asserts the existence of certain species (sets) corresponding to properties of natural numbers. In the intuitionistic theory of sequences of natural numbers there is an analoguous principle, implicit in Brouwer's writing and explicitly stated by Kripke, which asserts the existence of certain sequences corresponding to statements. The justification of this principle, Kripke's Schema, makes use of the concept of the so-called creative subject. For more information the reader is referred to Troelstra [5].

Kripke's Schema reads

There is a weaker version

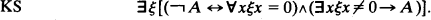
The idea to reduce species to sequences via Kripke's schema occurred several years ago (cf. [2, p. 128], [5, p. 104]). In [1] the reduction technique was applied in the construction of a model for HAS.

On second thought, however, I realized that there is a straightforward, simpler way to exploit Kripke's schema, avoiding models altogether. The idea to present this material separately was forced on the author by C. Smorynski.

Consider a second order arithmetic with both species and sequence variables. By KS we have

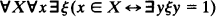
(for convenience we restrict ourselves in KS to 0-1-sequences). An application of AC-NF gives

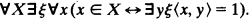
Of course ξ is not uniquely determined. This is the key to the reduction of full second order arithmetic, or HAS, to a theory of sequences.

We now introduce a translation τ to eliminate species variables. It is no restriction to suppose that the formulae contain only the sequence variables ξ1, ξ3, ξ5, …

Note that by virtue of the definition of τ the axiom of extensionality is automatically verified after translation. The translation τ eliminates the species variables and leaves formulae without species variables invariant.