Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MATET, Pierre
2006.
Covering for category and combinatorics on $P_\kappa(\lambda)$.
Journal of the Mathematical Society of Japan,
Vol. 58,
Issue. 1,
Matet, Pierre
2022.
Piece selection and cardinal arithmetic.
Mathematical Logic Quarterly,
Vol. 68,
Issue. 4,
p.
416.

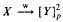 that is a weakening of the usual partition relation
that is a weakening of the usual partition relation 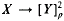 . Our main result asserts that if κ is an uncountable strongly compact cardinal and
. Our main result asserts that if κ is an uncountable strongly compact cardinal and 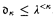 , then
, then 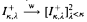 does not hold.
does not hold.