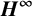 ${\boldsymbol H}^{\boldsymbol{\infty}}$ MAPS
${\boldsymbol H}^{\boldsymbol{\infty}}$ MAPSPublished online by Cambridge University Press: 12 May 2021
Let 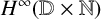 $H^\infty ({\mathbb {D}}\times {\mathbb {N}})$
be the Banach algebra of bounded holomorphic functions defined on the disjoint union of countably many copies of the open unit disk
$H^\infty ({\mathbb {D}}\times {\mathbb {N}})$
be the Banach algebra of bounded holomorphic functions defined on the disjoint union of countably many copies of the open unit disk 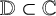 ${\mathbb {D}}\subset {{\mathbb C}}$
. We show that the dense stable rank of
${\mathbb {D}}\subset {{\mathbb C}}$
. We show that the dense stable rank of 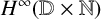 $H^\infty ({\mathbb {D}}\times {\mathbb {N}})$
is
$H^\infty ({\mathbb {D}}\times {\mathbb {N}})$
is 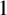 $1$
and, using this fact, prove some nonlinear Runge-type approximation theorems for
$1$
and, using this fact, prove some nonlinear Runge-type approximation theorems for 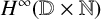 $H^\infty ({\mathbb {D}}\times {\mathbb {N}})$
maps. Then we apply these results to obtain a priori uniform estimates of norms of approximating maps in similar approximation problems for the algebra
$H^\infty ({\mathbb {D}}\times {\mathbb {N}})$
maps. Then we apply these results to obtain a priori uniform estimates of norms of approximating maps in similar approximation problems for the algebra 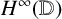 $H^\infty ({\mathbb {D}})$
.
$H^\infty ({\mathbb {D}})$
.
Communicated by Finnur Larusson
This research is supported in part by NSERC Grant No. 10010444.