Article contents
GRADIENT FLOWS OF HIGHER ORDER YANG–MILLS–HIGGS FUNCTIONALS
Published online by Cambridge University Press: 31 May 2021
Abstract
In this paper, we define a family of functionals generalizing the Yang–Mills–Higgs functionals on a closed Riemannian manifold. Then we prove the short-time existence of the corresponding gradient flow by a gauge-fixing technique. The lack of a maximum principle for the higher order operator brings us a lot of inconvenience during the estimates for the Higgs field. We observe that the 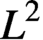 $L^2$-bound of the Higgs field is enough for energy estimates in four dimensions and we show that, provided the order of derivatives appearing in the higher order Yang–Mills–Higgs functionals is strictly greater than one, solutions to the gradient flow do not hit any finite-time singularities. As for the Yang–Mills–Higgs k-functional with Higgs self-interaction, we show that, provided
$L^2$-bound of the Higgs field is enough for energy estimates in four dimensions and we show that, provided the order of derivatives appearing in the higher order Yang–Mills–Higgs functionals is strictly greater than one, solutions to the gradient flow do not hit any finite-time singularities. As for the Yang–Mills–Higgs k-functional with Higgs self-interaction, we show that, provided 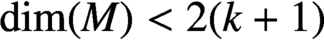 $\dim (M)<2(k+1)$, for every smooth initial data the associated gradient flow admits long-time existence. The proof depends on local
$\dim (M)<2(k+1)$, for every smooth initial data the associated gradient flow admits long-time existence. The proof depends on local 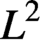 $L^2$-derivative estimates, energy estimates and blow-up analysis.
$L^2$-derivative estimates, energy estimates and blow-up analysis.
Keywords
Information
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 113 , Issue 2 , October 2022 , pp. 257 - 287
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Graeme Wilkin
The author is supported by the Natural Science Foundation of Universities of Anhui Province (Grant Number K120431039). The author is partially supported by the National Natural Science Foundation of China (Grant Numbers 11625106, 11721101, 12001548 and 11701580). The research is partially supported by the project ‘Analysis and Geometry on Bundle’ of the Ministry of Science and Technology of the People’s Republic of China (Grant Number SQ2020YFA070080).
References
 ${\int}_m{\left| rm\right|}^2$
’,
J. Geom. Anal.
18(1) (2008), 249–271.CrossRefGoogle Scholar
${\int}_m{\left| rm\right|}^2$
’,
J. Geom. Anal.
18(1) (2008), 249–271.CrossRefGoogle Scholar- 1
- Cited by


