Hostname: page-component-7dd5485656-frp75 Total loading time: 0 Render date: 2025-10-31T14:59:08.931Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE PRODUCT OF ELEMENTS WITH PRESCRIBED TRACE

Part of: General field theory Geometry Finite geometry and special incidence structures Linear incidence geometry

Published online by Cambridge University Press:  14 May 2020

JOHN SHEEKEY Open the ORCID record for JOHN SHEEKEY [Opens in a new window] ,
GEERTRUI VAN DE VOORDE Open the ORCID record for GEERTRUI VAN DE VOORDE [Opens in a new window]  and
JOSÉ FELIPE VOLOCH Open the ORCID record for JOSÉ FELIPE VOLOCH [Opens in a new window]
JOHN SHEEKEY
Affiliation:
University College Dublin, School of Mathematics and Statistics, Science Centre, East Belfield, Dublin 4, Ireland email: john.sheekey@ucd.ie
GEERTRUI VAN DE VOORDE
Affiliation:
School of Mathematics and Statistics,University of Canterbury, Private Bag 4800,Christchurch 8140, New Zealand email: geertrui.vandevoorde@canterbury.ac.nz
JOSÉ FELIPE VOLOCH*
Affiliation:
School of Mathematics and Statistics,University of Canterbury, Private Bag 4800,Christchurch 8140, New Zealand
*
email: felipe.voloch@canterbury.ac.nz
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper deals with the following problem. Given a finite extension of fields 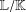$\mathbb{L}/\mathbb{K}$ and denoting the trace map from 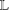$\mathbb{L}$ to 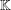$\mathbb{K}$ by 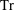$\text{Tr}$, for which elements $z$ in 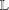$\mathbb{L}$, and $a$, 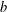$b$ in 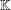$\mathbb{K}$, is it possible to write $z$ as a product 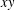$xy$, where 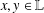$x,y\in \mathbb{L}$ with 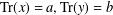$\text{Tr}(x)=a,\text{Tr}(y)=b$? We solve most of these problems for finite fields, with a complete solution when the degree of the extension is at least 5. We also have results for arbitrary fields and extensions of degrees 2, 3 or 4. We then apply our results to the study of perfect nonlinear functions, semifields, irreducible polynomials with prescribed coefficients, and a problem from finite geometry concerning the existence of certain disjoint linear sets.

Keywords

field extensiontracePN functionlinear set

MSC classification

Primary: 12E20: Finite fields (field-theoretic aspects)
Secondary: 51E20: Combinatorial structures in finite projective spaces 51A35: Non-Desarguesian affine and projective planes

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 112 , Issue 2 , April 2022 , pp. 264 - 288
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by M. Coons

References

Ball, S., Blokhuis, A. and Lavrauw, M., ‘Linear (q + 1)-fold blocking sets in PG(2, q 4)’, Finite Fields Appl. 6(4) (2000), 294–301.CrossRefGoogle Scholar
Ball, S., Ebert, G. and Lavrauw, M., ‘A geometric construction of finite semifields’, J. Algebra 311(1) (2007), 117–129.CrossRefGoogle Scholar
Coulter, R. and Henderson, M., ‘On a conjecture on planar polynomials of the form x (Tr(x) - ux)’, Finite Fields Appl. 21 (2013), 30–34.CrossRefGoogle Scholar
De Boeck, M. and Van de Voorde, G., ‘A linear set view on KM-arcs’, J. Algebraic Combin. 44(1) (2016), 131–164.CrossRefGoogle Scholar
Dummit, D. and Foote, R., Abstract Algebra, 3rd edn (Wiley, Hoboken, NJ, 2004).Google Scholar
Ha, J., ‘Irreducible polynomials with several prescribed coefficients’, Finite Fields Appl. 40 (2016), 10–25.CrossRefGoogle Scholar
Ham, K. and Mullen, G., ‘Distribution of irreducible polynomials of small degrees over finite fields’, Math. Comp. 67(221) (1998), 337–341.CrossRefGoogle Scholar
Kyureghyan, G. and Ozbudak, F., Planar Products of Linearized Polynomials. WCC 2011 – Workshop on Coding and Cryptography, April 2011, Paris, France (2011), 351–360, inria-00614431.Google Scholar
Lavrauw, M. and Sheekey, J., ‘The BEL-rank of finite semifields’, Des. Codes Cryptogr. 84(3) 345–358.CrossRefGoogle Scholar
Lavrauw, M. and Van de Voorde, G., ‘Field reduction in finite geometry’, in: Topics in Finite Fields, Contemporary Mathematics, 632 (American Mathematical Society, Providence, RI, 2015).Google Scholar
Lunardon, G., ‘Linear k-blocking sets’, Combinatorica 21(4) (2001), 571–581.CrossRefGoogle Scholar
Panario, D. and Tzanakis, G., ‘A generalization of the Hansen–Mullen conjecture on irreducible polynomials over finite fields’, Finite Fields Appl. 18(2) (2012), 303–315.CrossRefGoogle Scholar
Polverino, O., ‘Linear sets in finite projective spaces’, Discrete Math. 310(22) (2010), 3096–3107.CrossRefGoogle Scholar
Stichtenoth, H., Algebraic Function Fields and Codes, Universitext (Springer, Berlin, 1993).Google Scholar
Yang, M., Zhua, S. and Feng, K., ‘Planarity of mappings x (Tr(x) - (𝛼/2)x) on finite fields’, Finite Fields Appl. 23 (2013), 1–7.CrossRefGoogle Scholar
Wan, D., ‘Generators and irreducible polynomials over finite fields’, Math. Comput. 66(219) (1997), 1195–1212.CrossRefGoogle Scholar