Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-08T12:49:24.186Z Has data issue: false hasContentIssue false
  • English
  • Français

$\boldsymbol{C}^*$-ALGEBRAS ASSOCIATED WITH TWO-SIDED SUBSHIFTS

Part of: Selfadjoint operator algebras Topological dynamics Ergodic theory

Published online by Cambridge University Press:  18 January 2021

KENGO MATSUMOTO
KENGO MATSUMOTO*
Affiliation:
Department of Mathematics, Joetsu University of Education, Joetsu943-8512, Japan
*
e-mail: kengo@juen.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is a continuation of the paper, Matsumoto [‘Subshifts, 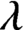$\lambda $ -graph bisystems and $C^*$ -algebras’, J. Math. Anal. Appl. 485 (2020), 123843]. A 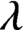$\lambda $ -graph bisystem consists of a pair of two labeled Bratteli diagrams satisfying a certain compatibility condition on their edge labeling. For any two-sided subshift 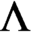$\Lambda $ , there exists a 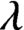$\lambda $ -graph bisystem satisfying a special property called the follower–predecessor compatibility condition. 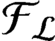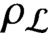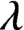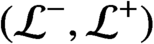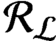We construct an AF-algebra ${\mathcal {F}}_{\mathcal {L}}$ with shift automorphism $\rho _{\mathcal {L}}$ from a $\lambda $ -graph bisystem $({\mathcal {L}}^-,{\mathcal {L}}^+)$ , and define a $C^*$ -algebra ${\mathcal R}_{\mathcal {L}}$ by the crossed product 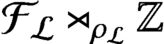. It is a two-sided subshift analogue of asymptotic Ruelle algebras constructed from Smale spaces. If 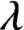$\lambda $ -graph bisystems come from two-sided subshifts, these $C^*$ -algebras are proved to be invariant under topological conjugacy of the underlying subshifts. We present a simplicity condition of the $C^*$ -algebra 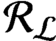${\mathcal R}_{\mathcal {L}}$ and the K-theory formulas of the $C^*$ -algebras 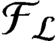${\mathcal {F}}_{\mathcal {L}}$ and 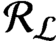${\mathcal R}_{\mathcal {L}}$ . The K-group for the AF-algebra 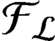${\mathcal {F}}_{\mathcal {L}}$ is regarded as a two-sided extension of the dimension group of subshifts.

Keywords

AF-algebraBratteli diagramC*-algebracrossed productdimension groupK-groupRuelle algebraSmale spacesubshifttopological conjugacy

MSC classification

Primary: 37A55: Relations with the theory of $C^*$-algebras
Secondary: 46L55: Noncommutative dynamical systems 37B10: Symbolic dynamics
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 112 , Issue 2 , April 2022 , pp. 230 - 263
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Communicated by Lisa Orloff Clark

The author was supported by JSPS KAKENHI Grant Nos. 15K04896 and 19K03537.

References

Bates, T. and Pask, D., ‘ ${\mathrm{C}}^{\ast }$ -algebras of labeled graphs’, J. Operator Theory 57 (2007), 207–226.Google Scholar
Bratteli, O., ‘Inductive limits of finite-dimensional ${\mathrm{C}}^{\ast }$ -algebras’, Trans. Amer. Math. Soc. 171 (1972), 195–234.Google Scholar
Cuntz, J. and Krieger, W., ‘A class of ${\mathrm{C}}^{\ast }$ -algebras and topological Markov chains’, Invent. Math. 56 (1980), 251–268.10.1007/BF01390048CrossRefGoogle Scholar
Fischer, R., ‘Sofic systems and graphs’, Monatsh. Math. 80 (1975), 179–186.10.1007/BF01319913CrossRefGoogle Scholar
Holton, C. G., ‘The Rohlin property for shifts of finite type’, J. Funct. Anal. 229 (2005), 277–299.CrossRefGoogle Scholar
Killough, D. B. and Putnam, I. F., ‘Ring and module structures on dimension groups associated with a shift of finite type’, Ergod. Th. & Dynam. Sys. 32 (2012), 1370–1399.10.1017/S0143385712000272CrossRefGoogle Scholar
Krieger, W., ‘On topological Markov chains’, in: Dynamical Systems, Vol. II Warsaw, Astérisque, 50 (Société Mathématique de France, Paris, 1977), 193–196.Google Scholar
Krieger, W., ‘On dimension functions and topological Markov chains’, Invent. Math. 56 (1980), 239–250.10.1007/BF01390047CrossRefGoogle Scholar
Krieger, W., ‘On dimension for a class of homeomorphism groups’, Math. Ann. 252 (1980), 87–95.10.1007/BF01420115CrossRefGoogle Scholar
Krieger, W., ‘On sofic systems I’, Israel J. Math. 48 (1984), 305–330.10.1007/BF02760631CrossRefGoogle Scholar
Krieger, W., ‘On sofic systems II’, Israel J. Math. 60 (1987), 167–176.10.1007/BF02790789CrossRefGoogle Scholar
Kumjian, A., Pask, D., Raeburn, I. and Renault, J., ‘Graphs, groupoids and Cuntz–Krieger algebras’, J. Funct. Anal. 144 (1997), 505–541.10.1006/jfan.1996.3001CrossRefGoogle Scholar
Lind, D. and Marcus, B., An Introduction to Symbolic Dynamics and Coding (Cambridge University Press, Cambridge, 1995).CrossRefGoogle Scholar
Matsumoto, K., ‘Presentations of subshifts and their topological conjugacy invariants’, Doc. Math. 4 (1999), 285–340.Google Scholar
Matsumoto, K., ‘ ${C}^{\ast }$ -algebras associated with presentations of subshifts’, Doc. Math. 7 (2002), 1–30.Google Scholar
Matsumoto, K., ‘Actions of symbolic dynamical systems on ${C}^{\ast }$ -algebras’, J. reine angew. Math. 605 (2007), 23–49.Google Scholar
Matsumoto, K., ‘Orbit equivalence in ${C}^{\ast }$ -algebras defined by actions of symbolic dynamical systems’, Contemp. Math. 503 (2009), 121–140.10.1090/conm/503/09896CrossRefGoogle Scholar
Matsumoto, K., ‘Actions of symbolic dynamical systems on ${{C}}^{\ast }$ -algebras II. Simplicity of ${{C}}^{\ast }$ -symbolic crossed products and some examples’, Math. Z. 265 (2010), 735–760.10.1007/s00209-009-0538-3CrossRefGoogle Scholar
Matsumoto, K., ‘Asymptotic continuous orbit equivalence of Smale spaces and Ruelle algebras,’ Canad. J. Math. 71 (2019), 1243–1296.10.4153/CJM-2018-012-xCrossRefGoogle Scholar
Matsumoto, K., ‘Topological conjugacy of topological Markov shifts and Ruelle algebras’, J. Operator Theory 82 (2019), 253–284.Google Scholar
Matsumoto, K., ‘Subshifts, $\lambda$ -graph bisystems and ${C}^{\ast }$ -algebras’, J. Math. Anal. Appl. 485 (2020), 123843.10.1016/j.jmaa.2020.123843CrossRefGoogle Scholar
Matsumoto, K., Flip conjugacy and asymptotic continuous orbit equivalence of Smale spaces, Preprint, 2019, arXiv:1906.08441[math.OA].10.4153/CJM-2018-012-xCrossRefGoogle Scholar
Matsumoto, K., An étale equivalence relation on a configuration space arising from a subshift and related ${C}^{\ast }$ -algebras, Preprint, 2019, arXiv:1912.07216[math.OA].Google Scholar
Matsumoto, K., Simple purely infinite ${C}^{\ast }$ -algebras associated with normal subshifts, Preprint, 2020, arXiv:2003.11711v2[mathOA].Google Scholar
Nasu, M., ‘Topological conjugacy for sofic shifts’, Ergod. Th. & Dynam. Sys. 6 (1986), 265–280.CrossRefGoogle Scholar
Nasu, M., ‘Textile systems for endomorphisms and automorphisms of the shift’, Mem. Amer. Math. Soc. 114 (1995), 546.Google Scholar
Pimsner, M. and Voiculescu, D., ‘Exact sequences for K-groups and Ext-groups of certain cross-products ${{C}}^{\ast }$ -algebras’, J. Operator Theory 4 (1980), 93–118.Google Scholar
Putnam, I. F., ‘ ${{C}}^{\ast }$ -algebras from Smale spaces’, Canad. J. Math. 48 (1996), pp. 175–195.CrossRefGoogle Scholar
Putnam, I. F., Hyperbolic Systems and Generalized Cuntz–Krieger Algebras, Lecture Notes (Summer School in Operator Algebras, Odense, 1996).Google Scholar
Putnam, I. F. and Spielberg, J., ‘The structure of ${{C}}^{\ast }$ -algebras associated with hyperbolic dynamical systems’, J. Funct. Anal. 163 (1999), 279–299.10.1006/jfan.1998.3379CrossRefGoogle Scholar
Ruelle, D., ‘Non-commutative algebras for hyperbolic diffeomorphisms’, Invent. Math. 93 (1988), 1–13.CrossRefGoogle Scholar
Thomsen, K., ‘ ${{C}}^{\ast }$ -algebras of homoclinic and heteroclinic structure in expansive dynamics’, Mem. Amer. Math. Soc. 206 (2010), 970.Google Scholar
Weiss, B., ‘Subshifts of finite type and sofic systems’, Monatsh. Math. 77 (1973), 462–474.10.1007/BF01295322CrossRefGoogle Scholar
Williams, R. F., ‘Classification of subshifts of finite type’, Ann. of Math. 98 (1973), 120–153. Erratum, Ann. of Math. 99 (1974), 380–381.10.2307/1970908CrossRefGoogle Scholar