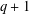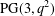Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Innamorati, Stefano
and
Zuanni, Fulvio
2020.
A combinatorial characterization of the Baer and the unital cone in $$PG(3,q^2)$$.
Journal of Geometry,
Vol. 111,
Issue. 3,
Aguglia, Angela
and
Pavese, Francesco
2020.
On non-singular Hermitian varieties of PG(4,q2).
Discrete Mathematics,
Vol. 343,
Issue. 1,
p.
111634.
Aguglia, Angela
Giuzzi, Luca
Montinaro, Alessandro
and
Siconolfi, Viola
2025.
On Quasi‐Hermitian Varieties in Even Characteristic and Related Orthogonal Arrays.
Journal of Combinatorial Designs,
Vol. 33,
Issue. 3,
p.
109.