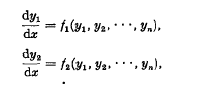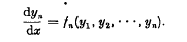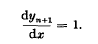Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Butcher, J. C.
1964.
Integration processes based on Radau quadrature formulas.
Mathematics of Computation,
Vol. 18,
Issue. 86,
p.
233.
Butcher, J. C.
1964.
Implicit Runge-Kutta processes.
Mathematics of Computation,
Vol. 18,
Issue. 85,
p.
50.
Butcher, J. C.
1965.
On the attainable order of Runge-Kutta methods.
Mathematics of Computation,
Vol. 19,
Issue. 91,
p.
408.
Shintani, Hisayoshi
1966.
Two-step processes by one-step methods of order 3 and of order 4.
Hiroshima Mathematical Journal,
Vol. 30,
Issue. 2,
Glasmacher, Werner
and
Sommer, Dietmar
1966.
Implizite Runge-Kutta-Formeln.
p.
17.
Casadei, G.
1966.
Osservazioni sulla scelta dei coeficienti del metodo di Runge-Kutta per la soluzione di sistemi di equazioni differenziali ordinarie.
Calcolo,
Vol. 2,
Issue. S1,
p.
205.
Cooper, G. J.
1967.
A class of single-step methods for systems of nonlinear differential equations.
Mathematics of Computation,
Vol. 21,
Issue. 100,
p.
597.
Sarafyan, Diran
and
Brown, Robert
1967.
Computer derivation of algebraic equations associated with runge-kutta formulas.
BIT,
Vol. 7,
Issue. 2,
p.
156.
Cooper, G. J.
and
Gal, E.
1967.
Single step methods for linear differential equations.
Numerische Mathematik,
Vol. 10,
Issue. 4,
p.
307.
Cooper, G. J.
1968.
Interpolation and quadrature methods for ordinary differential equations.
Mathematics of Computation,
Vol. 22,
Issue. 101,
p.
69.
Prothero, A.
1969.
Conference on the Numerical Solution of Differential Equations.
Vol. 109,
Issue. ,
p.
228.
Fehlberg, E.
1969.
Klassische Runge-Kutta-Formeln fünfter und siebenter Ordnung mit Schrittweiten-Kontrolle.
Computing,
Vol. 4,
Issue. 2,
p.
93.
Zeller, Karl
1969.
Abstract Spaces and Approximation / Abstrakte Räume und Approximation.
Vol. 10,
Issue. ,
p.
365.
Curtis, A. R.
1970.
An eighth order Runge-Kutta process with eleven function evaluations per step.
Numerische Mathematik,
Vol. 16,
Issue. 3,
p.
268.
Stetter, Hans J.
1971.
Local Estimation of the Global Discretization Error.
SIAM Journal on Numerical Analysis,
Vol. 8,
Issue. 3,
p.
512.
1971.
Numerical Solution of Ordinary Differential Equations.
Vol. 74,
Issue. ,
p.
39.
Kastlunger, K. H.
and
Wanner, G.
1972.
Runge Kutta processes with multiple nodes.
Computing,
Vol. 9,
Issue. 1,
p.
9.
Scherer, Rudolf
1972.
Herleitung von Runge-Kutta-Verfahren der Ordnung vier mit �bersichtlichen Fehlerdarstellungen.
Mathematische Zeitschrift,
Vol. 128,
Issue. 4,
p.
311.
Cooper, G. J.
and
Verner, J. H.
1972.
Some Explicit Runge”Kutta Methods of High Order.
SIAM Journal on Numerical Analysis,
Vol. 9,
Issue. 3,
p.
389.
Scherer, R.
1972.
Fehlerabschätzung für ein Runge-Kutta-Verfahren mit mehrfachen Knoten.
Computing,
Vol. 10,
Issue. 4,
p.
391.