Hostname: page-component-8448b6f56d-wq2xx Total loading time: 0 Render date: 2024-04-18T02:29:53.369Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPUTATION OF ZEROS OF MONOTONE TYPE MAPPINGS: ON CHIDUME’S OPEN PROBLEM

Part of: Nonlinear operators and their properties

Published online by Cambridge University Press:  05 February 2020

N. DJITTE Open the ORCID record for N. DJITTE [Opens in a new window] ,
J. T. MENDY  and
T. M. M. SOW
N. DJITTE*
Affiliation:
Gaston Berger University, Department of Applied Mathematics, Saint Louis, Senegal email ngalla.djitte@ugb.edu.sn
J. T. MENDY
Affiliation:
Gaston Berger University, Department of Applied Mathematics, Saint Louis, Senegal email jt.mendy@utg.edu.gm
T. M. M. SOW
Affiliation:
Gaston Berger University, Department of Applied Mathematics, Saint Louis, Senegal email sowthierno89@gmail.com
*
✉ngalla.djitte@ugb.edu.sn
Get access Rights & Permissions [Opens in a new window]

Abstract

For 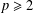$p\geq 2$, let $E$ be a 2-uniformly smooth and 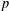$p$-uniformly convex real Banach space and let 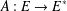$A:E\rightarrow E^{\ast }$ be a Lipschitz and strongly monotone mapping such that 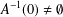$A^{-1}(0)\neq \emptyset$. For given 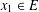$x_{1}\in E$, let 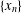$\{x_{n}\}$ be generated by the algorithm 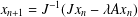$x_{n+1}=J^{-1}(Jx_{n}-\unicode[STIX]{x1D706}Ax_{n})$, 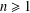$n\geq 1$, where 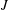$J$ is the normalized duality mapping from 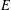$E$ into 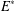$E^{\ast }$ and 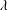$\unicode[STIX]{x1D706}$ is a positive real number in 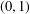$(0,1)$ satisfying suitable conditions. Then it is proved that 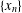$\{x_{n}\}$ converges strongly to the unique point 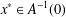$x^{\ast }\in A^{-1}(0)$. Furthermore, our theorems provide an affirmative answer to the Chidume et al. open problem [‘Krasnoselskii-type algorithm for zeros of strongly monotone Lipschitz maps in classical Banach spaces’, SpringerPlus4 (2015), 297]. Finally, applications to convex minimization problems are given.

Keywords

iterative algorithmstrongly monotone mappingsLipschitzconvex minimization problem

MSC classification

Primary: 47H05: Monotone operators and generalizations
Secondary: 47H07: Monotone and positive operators on ordered Banach spaces or other ordered topological vector spaces 47H04: Set-valued operators
Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 108 , Issue 2 , April 2020 , pp. 278 - 288
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This work is supported by the Center of Exellence CEA-MITIC, Gaston Berger University, Senegal.

References

Agarwal, R. P., O’Regan, D. and Sahu, D. R., Fixed Point Theory and Its Applications (Springer, New York, 2009).Google Scholar
Alber, Ya., ‘Metric and generalized projection operator in Banach space: properties and applications’, in: Theory and Applications of Nonlinear Operators of Accretive and Monotone Type (ed. Kartsatos, A. G.) (Marcel Dekker, New York, 1996), 15–50.Google Scholar
Alber, Ya. and Guerre-Delabiere, S., ‘On the projection methods for fixed point problems’, Analysis (Munich) 21(1) (2001), 17–39.Google Scholar
Alber, Ya. and Ryazantseva, I., Nonlinear Ill Posed Problems of Monotone Type (Springer, London, 2006).Google Scholar
Berinde, V., Iterative Approximation of Fixed Points, Lecture Notes in Mathematics (Springer, London, 2007).Google Scholar
Berinde, V., Maruster, S. and Rus, I. A., ‘An abstract point of view on iterative approximation of fixed points of nonself operators’, J. Nonlinear Convex Anal. 15(5) (2014), 851–865.Google Scholar
Brézis, H. and Lions, P. L., ‘Produits infinis de resolvents’, Israel J. Math. 29 (1978), 329–345.CrossRefGoogle Scholar
Browder, F. E., ‘Nonlinear mappings of nonexpansive and accretive type in Banach spaces’, Bull. Amer. Math. Soc. 73 (1967), 875–882.CrossRefGoogle Scholar
Bynum, W. L., ‘Weak parallelogram laws for Banach spaces’, Canad. Math. Bull. 19(3) (1976), 269–275.CrossRefGoogle Scholar
Censor, Y. and Reich, S., ‘Iterations of paracontractions and firmly nonexpansive operators with applications to feasibility and optimization’, Optimization 37(4) (1996), 323–339.CrossRefGoogle Scholar
Chidume, C. E., Geometric Properties of Banach Spaces and Nonlinear iterations, Lectures Notes in Mathematics, 1965 (Springer, London, 2009).CrossRefGoogle Scholar
Chidume, C. E., ‘An approximation method for monotone Lipschitzian operators in Hilbert-spaces’, J. Aust. Math. Soc. Ser. A 41 (1986), 59–63.CrossRefGoogle Scholar
Chidume, C. E., ‘Convergence theorems for asymptotically pseudo-contractive mappings’, Nonlinear Anal. 49 (2002), 1–11.CrossRefGoogle Scholar
Chidume, C. E., ‘Iterative approximation of fixed points of Lipschitzian strictly pseudo-contractive mappings’, Proc. Amer. Math. Soc. 99(2) (1987), 283–288.Google Scholar
Chidume, C. E. and Bashir, A., ‘Approximation of common fixed points for finite families of nonself asymptotically nonexpansive mappings in Banach spaces’, J. Math. Anal. Appl. 326 (2007), 960–973.CrossRefGoogle Scholar
Chidume, C. E., Bello, A. U. and Usman, B., ‘Krasnoselskii-type algorithm for zeros of strongly monotone Lipschitz maps in classical Banach spaces’, SpringerPlus 4 (2015), 297.CrossRefGoogle ScholarPubMed
Chidume, C. E. and Chidume, C. O., ‘Convergence theorems for fixed points of uniformly continuous generalized Phi-hemi-contractive mappings’, J. Math. Anal. Appl. 303 (2005), 545–554.CrossRefGoogle Scholar
Chidume, C. E. and Chidume, C. O., ‘Convergence theorem for zeros of generalized Phi-quasi-accretive operators’, Proc. Amer. Math. Soc. 134 (2006), 243–251.CrossRefGoogle Scholar
Chidume, C. E. and Osilike, M. O., ‘Iterative solutions of nonlinear accretive operator equations in arbitrary Banach spaces’, Nonlinear Anal. 36 (1999), 863–872.CrossRefGoogle Scholar
Cioranescu, I., Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems, Mathematics and Its Applications, 62 (Springer, Dordrecht, 1990).CrossRefGoogle Scholar
Deng, L., ‘On Chidume’s open question’, J. Math. Appl. 174(2) (1993), 441–449.Google Scholar
Diemling, K., Nonlinear Functional Analysis (Springer, Berlin–Heidelberg, 1985).CrossRefGoogle Scholar
Goebel, K. and Reich, S., Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings, Monographs and Textbooks in Pure and Applied Mathematics, 83 (Marcel Dekker, New York, 1984).Google Scholar
Kamimura, S. and Takahashi, W., ‘Strong convergence of proximal-type algorithm in Banach space’, SIAM J. Optim. 13(3) (2002), 938–945.CrossRefGoogle Scholar
Liu, L., ‘Ishikawa and Mann iterative process with errors for nonlinear strongly accretive mappings in Banach spaces’, J. Math. Anal. Appl. 194(1) (1995), 114–125.CrossRefGoogle Scholar
Martinet, B., ‘Regularization d’inéquations variationelles par approximations successives’, Revue Française d’Informatique et de Recherche Operationelle 4 (1970), 154–159.Google Scholar
Minty, G. J., ‘Monotone (nonlinear) operator in Hilbert space’, Duke Math. 29 (1962), 341–346.CrossRefGoogle Scholar
Moudafi, A., ‘Alternating CQ-algorithm for convex feasibility and split fixed-point problems’, J. Nonlinear Convex Anal. 15(4) (2004), 809–818.Google Scholar
Moudafi, A., ‘A relaxed alternating CQ-algorithm for convex feasibility problems’, Nonlinear Anal. 79 (2003), 117–121.CrossRefGoogle Scholar
Moudafi, A., ‘Proximal methods for a class of bilevel monotone equilibrium problems’, J. Global Optim. 47(2) (2010), 45–52.CrossRefGoogle Scholar
Moudafi, A. and Thera, M., ‘Finding a zero of the sum of two maximal monotone operators’, J. Optim. Theory Appl. 94(2) (1997), 425–448.CrossRefGoogle Scholar
Pascali, D. and Sburian, S., Nonlinear Mappings of Monotone Type (Editura Academiei, Bucharest, 1978).CrossRefGoogle Scholar
Qihou, L., ‘The convergence theorems of the sequence of Ishikawa iterates for hemi-contractive mapping’, J. Math. Anal. Appl. 148 (1990), 55–62.CrossRefGoogle Scholar
Reich, S., ‘Extension problems for accretive sets in Banach spaces’, J. Funct. Anal. 26 (1977), 378–395.CrossRefGoogle Scholar
Reich, S., Iterative Methods for Accretive Sets in Banach Spaces (Academic Press, New York, 1978), 317–326.Google Scholar
Reich, S., ‘Constructive techniques for accretive and monotone operators’, in: Applied Non-Linear Analysis (Academic Press, New York, 1979), 335–345.Google Scholar
Reich, S. and Sabach, S., ‘A strong convergence theorem for a proximal-type algorithm in reflexive Banach spaces’, J. Nonlinear Convex Anal. 10(3) (2009), 471–485.Google Scholar
Reich, S. and Sabach, S., ‘Two strong convergence theorems for a proximal method in reflexive Banach spaces’, Numer. Funct. Anal. Optim. 31(1-3) (2010), 22–44.CrossRefGoogle Scholar
Reich, S., ‘Strong convergent theorems for resolvents of accretive operators in Banach spaces’, J. Math. Anal. Appl. 75 (1980), 287–292.CrossRefGoogle Scholar
Rockafellar, R. T., ‘Monotone operator and the proximal point algorithm’, SIAM J. Control Optim. 14 (1976), 877–898.CrossRefGoogle Scholar
Takahashi, W. and Ueda, Y., ‘On Reich’s strong convergence theorems for resolvents of accretive operators’, J. Math. Anal. Appl. 104(2) (1984), 546–553.CrossRefGoogle Scholar
Weng, X. L., ‘Fixed point iteration for local strictly pseudo-contractive mappings’, Proc. Amer. Math. Soc. 113(3) (1991), 727–731.CrossRefGoogle Scholar
William, K. and Shahzad, N., Fixed Point Theory in Distance Spaces (Springer, Cham, 2014).Google Scholar
Xiao, R., ‘Chidume’s open problems and fixed point theorems’, Xichuan Daxue Xuebao 35(4) (1998), 505–508.Google Scholar
Xu, Z. B., ‘A note on the Ishikawa iteration schemes’, J. Math. Anal. Appl. 167 (1992), 582–587.CrossRefGoogle Scholar
Xu, Z. B. and Roach, G. F., ‘Characteristic inequalities for uniformly convex and uniformly smooth Banach space’, J. Math. Anal. Appl. 157 (1991), 189–210.CrossRefGoogle Scholar
Xu, Z. B., Jiang, Y. L. and Roach, G. F., ‘A further necessary and sufficient condition for strong convergence of nonlinear contraction semigroups and of iteration methods for accretive operators in Banach spaces’, Proc. Edinb. Math. Soc. 38(2) (1995), 1–12.CrossRefGoogle Scholar
Xu, H. K., ‘Inequalities in Banach spaces with applications’, Nonlinear Anal. 16(12) (1991), 1127–1138.CrossRefGoogle Scholar
Xu, Y., ‘Existence and convergence for fixed points of mappings of the asymptotically nonexpansive type’, Nonlinear Anal. 16 (1991), 1139–1146.CrossRefGoogle Scholar
Zhou, H. and Jia, Y., ‘Approximating the zeros of accretive operators by the Ishikawa iteration process’, Abstr. Appl. Anal. 1(2) (1996), 153–167.Google Scholar
Zhu, L., ‘Iteration solution of nonlinear equations involving m-accretive operators in Banach spaces’, J. Math. Anal. Appl. 188 (1994), 410–415.Google Scholar